PHÒNG GD TP NAM ĐỊNH
TRƯỜNG THCS LÊ ĐỨC THỌ
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ II
NĂM HỌC 2022-2023
Môn: Toán- lớp 9
(Thời gian làm bài 120 phút)
Đề khảo sát gồm 2 trang
Phần I. Trắc nghiệm (2,0 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Biểu thức
x
2
x 1 2019 xa6c đi8nh khi va: chi; khi
A. x 2 . B. x
2.
C. x
1.
D.
x
.
Câu 2. Cho đường thẳng (d): y 2x b 1 đi qua điêm A (1; 2) . Tung đô gôc cua đương thăng (d) la:
A. 0. B. 1. C. 3. D. 4.
Câu 3. Hai đội công nhân làm chung một công việc trong 2 ngày thì được 25% công việc. Thời gian hai
đội cu:ng la:m (với năng suất không đổi) để hoa:n tha:nh công việc đó la:
A. 4 ngày. B. 5 ngày. C. 6 ngày. D. 8 ngày.
Câu 4. Ha:m số na:o sau đây đồng biến khi x > 0?
A. y
a
2
1
x2 . B. y
a
2
1
x2 . C. y
a
1
2
x2 . D. y
a
1
2
x2 .
Câu 5. Phương trình
4x
2
2ax a2 2a 0 có nghiêm x 1 khi va chi khi
A. a
2.
B. a
2.
C. a 2 2
2.
D. a
2.
Câu 6. Cho tam giác ABC có AB = 6cm, BC = 10cm, AC = 8cm. Ba6n kính đường tròn ngoại tiếp tam gia6c
có độ da:i là
A. 3cm. B. 4cm. C. 5cm. D. 10cm.
Câu 7. Cho đường tròn (O; 15cm) va: dây AB = 24cm. Khoảng ca6ch từ tâm O đến dây AB la:
A. 7,5cm. B. 9cm. C. 12cm. D. 3
41
cm.
Câu 8. Cho hai đường tròn (O; 5cm) va: (O'; 3cm). Hai đường tròn tiếp xúc ngoa:i khi va: chi; khi
A. OO' = 8cm. B. OO' > 8cm. C. OO' = 2cm. D. OO' < 2cm.
Phần II. Tự luận (8,0 điểm)
Câu 9. (1,5 điểm) Cho biểu thức P =
1) Rút gọn P.
x
x
4
x
x
2
1
x 2
x
với x 0; x
4
.
2) Tìm số nguyên x nho; nhất để P < 0.
Câu 10. (1,5 điểm) Hai ô tô cu:ng khởi ha:nh từ hai đi8a điểm A va: B ca6ch nhau 210 km đi ngược chiều
nhau sau 3 giờ chúng gặp nhau. Tính vận tốc mỗi ô tô , biết rằng mỗi giờ ô tô đi từ A đi nhanh hơn ô tô đi
từ B là 10km.
ĐỀ CHÍNH
Câu 11. ( 1,0 điểm) Giải hệ phương trình
3 2 2 3
1
6 4 2 7
1
y x x y
x y
y x x
x y
− −
− =
+
−
− =
+
Câu 12. (3,0 điểm) Cho đường tròn (O) đường kính AB, dây CF vuông góc với OA tại H (H không trung
vơi A và O). Gọi I la: trung điểm của CH, AI cắt đường tròn (O) tại D. Gọi M la: giao điểm của AC va: BD,
N la: giao điểm của AD va: BC, K la: trung điểm của MN.
1) Chứng minh AC2 = AI.AD.
2) Chứng minh KC la: tiếp tuyến của đường tròn (O).
3) Gọi P là giao điểm của KC với tiếp tuyến tại A đường tròn (O). Chứng minh B, I, P thẳng ha:ng.
Câu 13. (1,0 điểm) Giải phương trình x
5
x 1 6 .
------------------HẾT-----------------
III. HƯỚNG DẪN CHẤM
PHÒNG GD&ĐT TP NAM ĐỊNH
TRƯỜNG THCS LÊ ĐỨC THỌ
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ II
NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 9
I. HƯỚNG DẪN CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày, nếu học sinh
giải theo cách khác mà đúng và đủ các bước thi9 cho điểm tương đương.
- Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn.
II. ĐÁP ÁN VÀ BIỂU ĐIỂM:
Phần I - Trắc nghiệm (2,0 điểm) Mỗi câu đúng cho 0,25 điểm.
Câu 1 2 3 4 5 6 7 8
Đáp án C A D B D C B A
Phần II – Tự luận (8,0 điểm)
Câu Ý Nội dung Điểm
1.
(1,5đ)
1)
(1,0đ) Với
0; 4x x
>
ta co6: P =
1
42 2
x x
xx x x
+ −
−+ −
( )
1 1 1
4 4
2 2 2
2
x x x
x x
x x x
x x
= + − = + +
− −
− + −
+
0,25
( ) ( ) ( ) ( ) ( ) ( )
2 2
2 2 2 2 2 2
x x x
x x x x x x
− +
= + +
− + − + − +
0,25
( ) ( ) ( )
( ) ( )
2
2
2 2 2 2
x x
x x
x x x x
+
+
= =
− + − +
0,25
2
x
x
=−
. Vâ8y P
2
x
x
=−
vơ6i
0; 4x x>
0,25
2)
(0,5đ)
Với
ta co6:
P < 0
0 2 0
2
xx
x
< − <
−
2 4x x < <
.
0,25
Kê6t hơ8p vơ6i
ta co6
{ }
1;2;3x
Vâ8y gia6 tri8 nguyên nho; nhâ6t cu;a x đê; P < 0 la: x = 1.
0,25
2.
(1,5đ)
Gọi x và y lần lượt là vâ8n tô6c cu;a ô tô đi tư: A va: ô tô đi tư: B
( đơn vi8: km/h; điê:u kiê8n: x > y > 0) 0,25
Hai ô tô cu:ng khởi hành từ hai địa điểm A và B cách nhau 210 km đi ngược
chiều nhau sau 3 giờ chúng gặp nhau nên ta có phương trình:
3x + 3y = 210
x + y = 70 (1)
0,25
Môyi giơ: ô tô đi từ A đi nhanh hơn ô tô đi từ B 10km nên ta có phương trình: x
- y = 10 (2) 0,25
Từ ( 1) và (2) ta có hệ phương trình
70
10
x y
x y
+ =
− =
Giải hệ tìm được x = 40; y = 30
0,5
Ta thâ6y x = 40; y = 30 tho;a mayn ca6c điê:u kiê8n cu;a â;n.
Vâ8y vâ8n tô6c cu;a ô tô đi tư: A va: B lâ:n lươ8t la: 40km/h va: 30km/h. 0,25
3.
(1,0đ)
ĐKXĐ:
1, 0
−
x y
. 0,25
Ta có :
3 2 2 3 2 2 3 2 2
3 1 3 2
1 1 1
y x x y y x x y x x
x y x y x y
− − − −
− = − + = − =
+ + +
0,25
Đặt
3 2 2
, =
1
y x x
u v
x y
−
=+
.
Hệ phương trình đã cho trở thành
2
2 7
u v
u v
− =
+ =
3
1
u
v
=
=
0,25
Suy ra
3 2 3
1
21
y x
x
x
y
−
=
+
=
5 3 3 3
2 6
x y x
y x y
− = − =
= =
Ta thấy x = 3, y = 6 thỏa mãn ĐKXĐ.
0,25
Vậy hệ phương trình đã cho có một nghiệm duy nhâ6t (x; y) = (3; 6).
4.
(3,0đ)
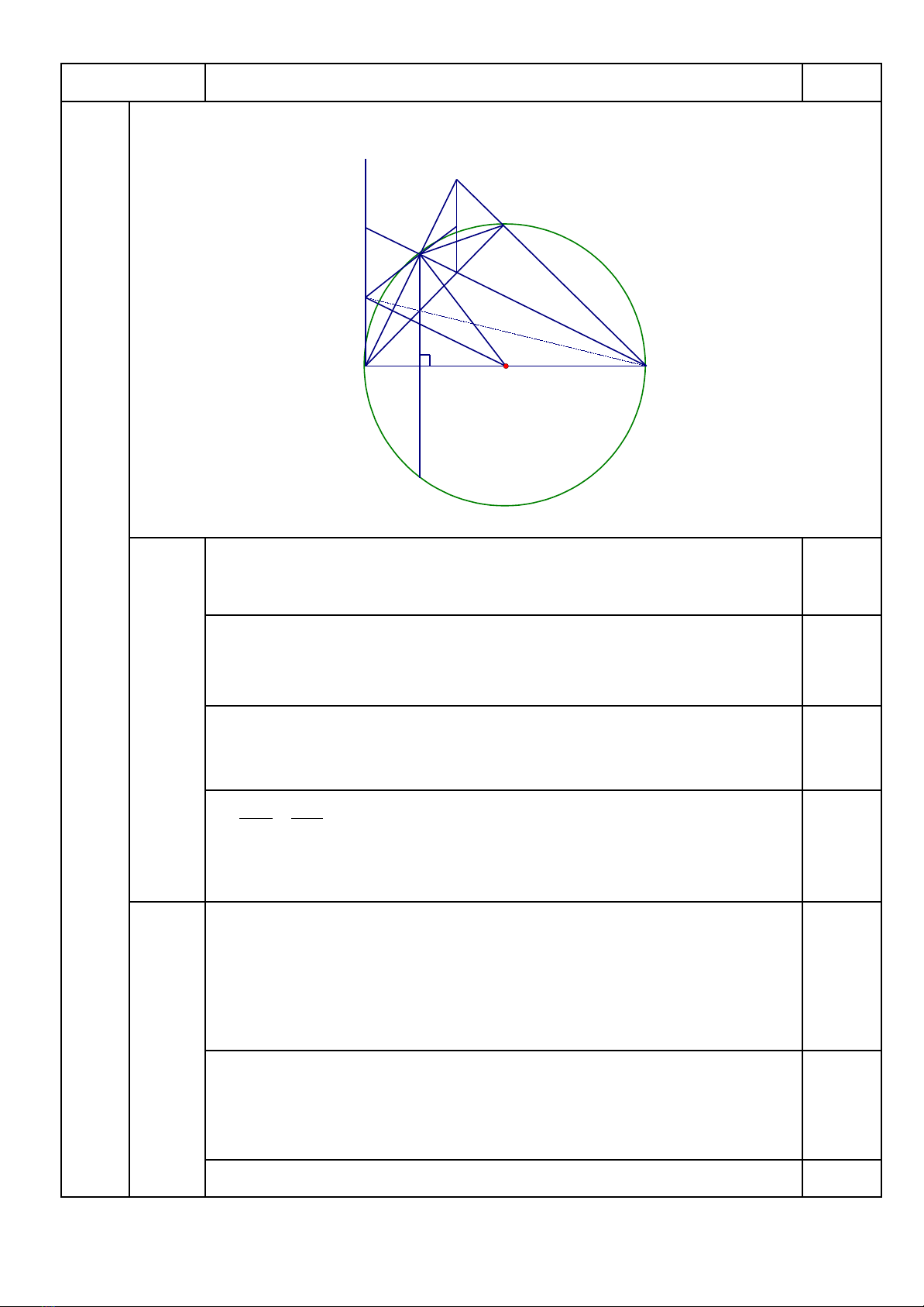
Hình vẽ:
E
Q
P
K
N
M
D
I
H
F
C
B
O
A
1)
(1,0đ)
Xét đường tròn (O) ta có AB
⊥
CF tại H (gt)
A là điểm chính giữa của cung nho; CF 0,25
ACF
=
ADC
(hai góc nội tiếp chắn hai cung bằng nhau)
hay
ACI
=
ADC
0,25
Xét ∆ ACI và ∆ADC có
ACI
=
ADC
(cmt) ;
CAD
chung
∆ ACI đồng dạng ∆ADC (g.g)
0,25
AC AI
=
AD AC
(cặp cạnh tương ứng)
hay AC2 = AI.AD.
0,25
2)
(1,0đ)
Xét đường tròn (O) ta có
ACB
=
ADB
= 900 (các góc nội tiếp chắn nửa
đường tròn).
AD
⊥
BM và BC
⊥
AM
N là trực tâm của ∆ABM
MN
⊥
AB
0,25
Ta có ∆CMN vuông tại C, K là trung điểm MN nên K là tâm đường tròn
ngoại tiếp ∆CMN
KC = KM
∆KCM cân tại K
KCM
=
KMC
(1).
0,25
Ta có OC = OA (bán kính đường tròn (O)) 0,25