Mã đề 122 Trang 1/5
S
Ở
GDĐT KON TUM
KI
Ể
M
GI
Ữ
A K
Ỳ
I
TRƯỜNG THCS VÀ THPT
LIÊN VIỆT KON TUM
ĐỀ CHÍNH THỨC
(Đề gồm có 05 trang)
NĂM HỌC 2024 – 2025
Môn: Toán; Lớp 12
Thời gian làm bài:90 phút, không kể thời gian phát đề.
Họ và tên: ............................................................................ Số báo danh: .......
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.
Câu 1. Đường tiệm cận xiên của đồ thị hàm số
1
2 3 1
f x x x
có phương trình là
A. 2y x. B. 2 3y x . C. 1x. D. 1y x .
Câu 2. Cho hàm số
f x có bảng xét dấu của đạo hàm như sau:
Hàm số
f x nghịch biến trên khoảng nào dưới đây?
A.
3;1. B.
; 3 . C.
3; . D.
1; .
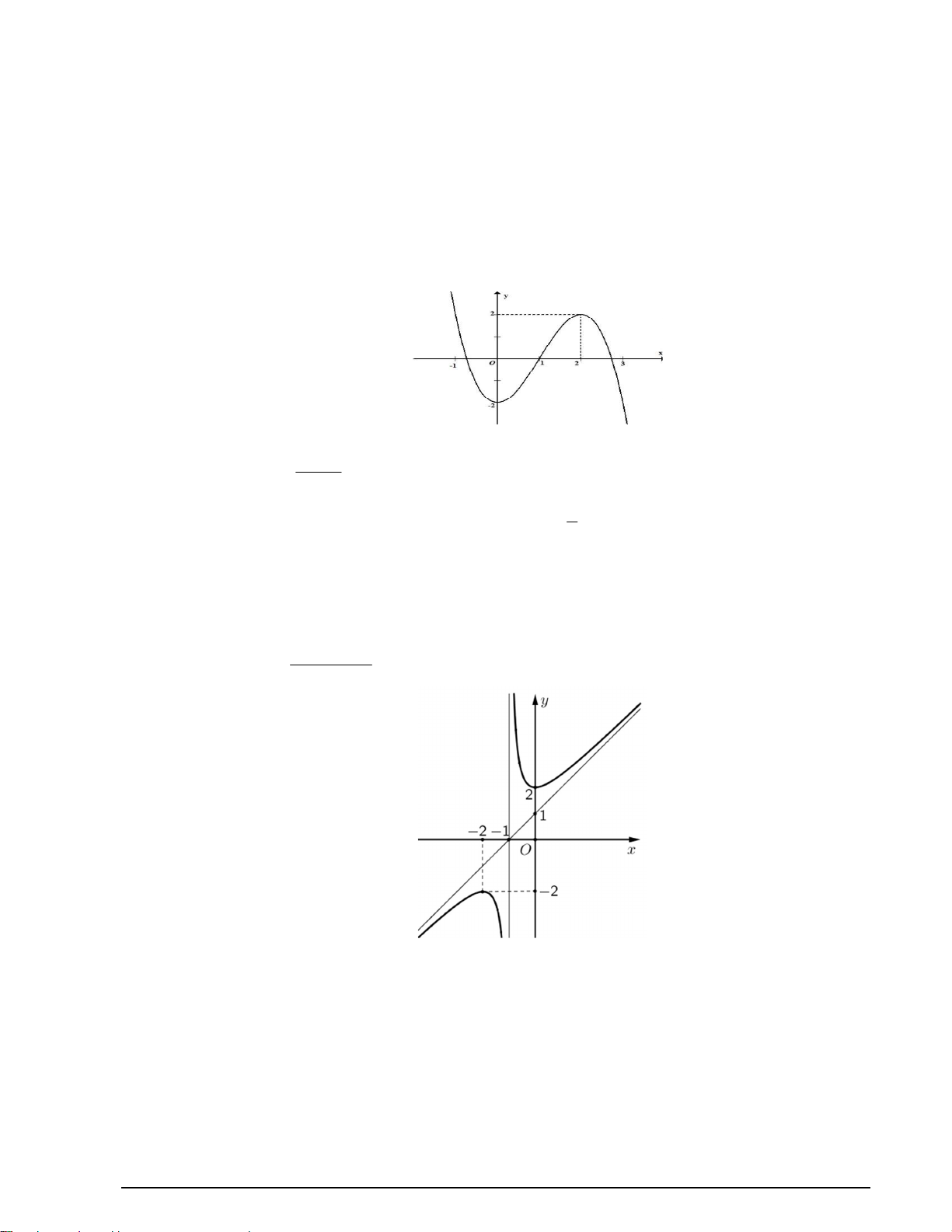
Câu 3. Hàm số 33 4y x x có điểm cực tiểu là
A. 6y. B. 2y. C. 1x. D. 1x .
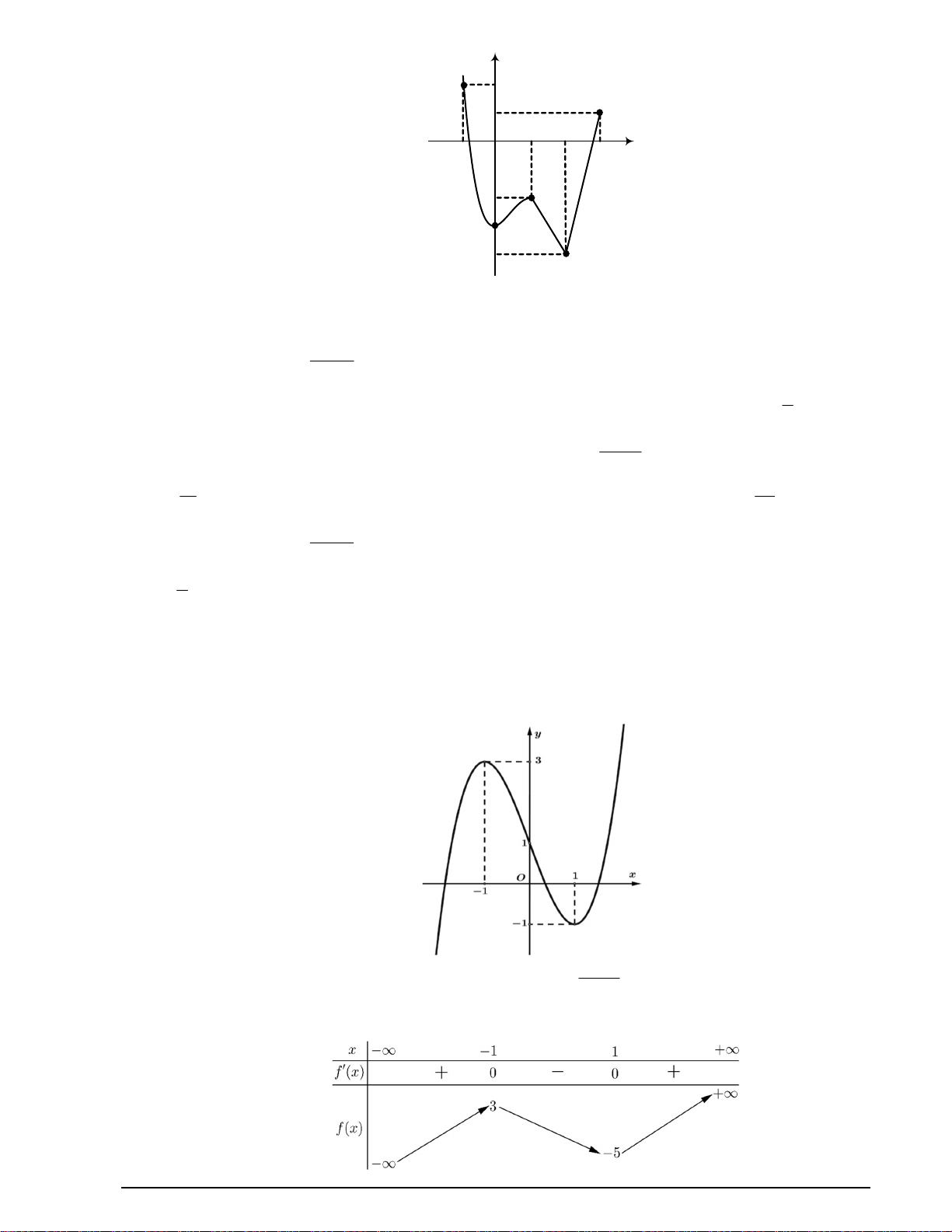
Câu 4. Cho hàm số
y f x
có đồ thị là đường cong trong hình vẽ dưới đây:
Hàm số
y f x có bao nhiêu điểm cực trị?
A. 3. B. 4. C. 1. D. 2.
Câu 5. Cho hàm số
y f x xác định trên
và
lim lim 4
x x
f x f x
 
. Phát biểu nào sau đây
đúng?
A. Đường thẳng 4x là tiệm cận ngang của đồ thị hàm số
y f x.
B. Đường thẳng 4y là tiệm cận đứng của đồ thị hàm số
y f x.
C. Đường thẳng 4y là tiệm cận ngang của đồ thị hàm số
y f x.
D. Đường thẳng 4x là tiệm cận đứng của đồ thị hàm số
y f x.
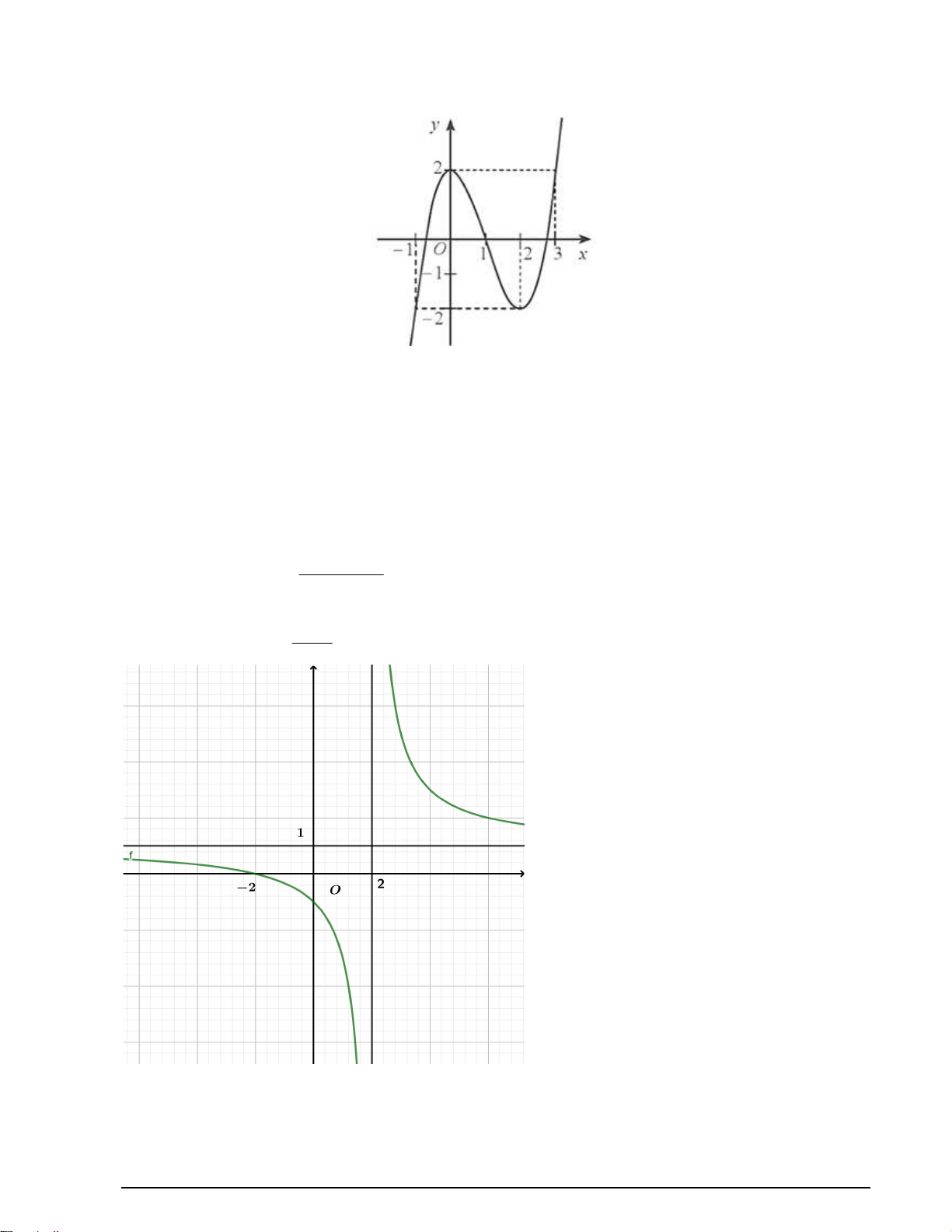
Câu 6. Cho hàm số
y f x liên tục trên đoạn
1;3 và có đồ thị như hình vẽ sau:
x
y
O
-1
1
y=f '(x)
4
Mã
đ
ề
122
Mã đề 122 Trang 2/5
1
2
3
1
2
3
4
x
y
O
2
1
Giá trị lớn nhất của hàm số trên đoạn
1;3bằng
A. 2. B. 1. C. 3. D. 1.
Câu 7. Đồ thị hàm số 2 3
2
x
yx
có đường tiệm cận đứng là
A. 2.x B. 2.y C. 2.x D. 3.
2
y
Câu 8. Tổng của giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 5
1
x
yx
trên đoạn
2;0 bằng
A. 11.
3
B. 5. C. 16. D. 26 .
3
Câu 9. Đồ thị hàm số 2 3
1
x
yx
cắt trục tung tại điểm có tọa độ là
A. 3;0
2
. B.
3;0. C.
0; 3 . D.
0; 3.
Câu 10. Cho hàm số 36y x x m thỏa mãn
1;0
max 10y
, với m là tham số thực. Khi đó m thuộc
khoảng
A.
1;4 . B.
4; . C.
; 3 . D.
3;1.
Câu 11. Đường cong trong hình vẽ sau đây là đồ thị của hàm số nào?
A. 33 1y x x . B. 33 1y x x . C. 2 1
1
x
yx
. D. 33 1y x x .
Câu 12. Cho hàm số
y f x có bảng biến thiên như sau:
Mã đề 122 Trang 3/5
Giá trị cực đại của hàm số đã cho bằng
A. 1. B. 3. C. 1. D. 5.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai.
Câu 1. Cho hàm số 3 2
3 2y x x .
a) Giá trị nhỏ nhất của hàm số trên đoạn
3;1 là 2.
b) Giá trị lớn nhất của hàm số trên đoạn
3;10 là (2)f.
c) Đạo hàm của hàm số đã cho là 2
3 6y x x
.
d) Đồ thị hàm số đã cho như ở hình sau.
Câu 2. Cho hàm số 3
2 2
x
yx
.
a) Đồ thị hàm số có đường tiệm cận ngang là đường thẳng 1
2
y.
b) Đồ thị hàm số có đường tiệm cận đứng là đường thẳng 1x .
c) Hàm số nghịch biến trên các khoảng
; 1 và
1;  .
d) Đồ thị hàm số có giao điểm I của hai đường tiệm cận nằm trên đường thẳng
: 2 3 0x y .
Câu 3.Cho hàm số
2
ax bx c
ymx n
có đồ thị như hình vẽ bên dưới.
a) Đồ thị hàm số đã cho có tiệm đứng 1x .
b) Trên khoảng
; 1 hàm số có giá trị lớn nhất bằng 2 .
c) Hàm số đã cho nghịch biến trên khoảng
2;0.
d) Gọi ( ; ), ( ; )
A A B B
A x y B x y là 2 điểm cực trị của đồ thị hàm số đã cho, khi đó 0
A B
y y .
Hình
Mã đề 122 Trang 4/5
Câu 4. Cho hàm số đa thức bậc ba
y f x
xác định trên
và có đồ thị như hình dưới đây.
a) Hàm số đã cho có
2
điểm cực trị.
b) Hàm số đã cho đồng biến trên các khoảng
;0
 và
2;

.
c) Điểm
0;2
M là điểm cực đại của đồ thị hàm số
( )
y f x
.
d) Hàm số
2
1
y f x x
nghịch biến trên khoảng
;
0 3
.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Đồ thị của hàm số 3 2
3 9 1
y x x x
có hai điểm cực trị là
A
và
B
. Tính độ dài đoạn thẳng
AB (làm tròn kết quả đến hàng phần chục).
Câu 2. Cho hàm số
2
2 3 4
5
x x
y
x
. Tiệm cận xiên của đồ thị hàm số đã cho có dạng
y ax b
.
Tính giá trị của biểu thức
2
S a b
.
Câu 3. Cho hàm số
2
ax
y
cx b
có đồ thị như hình vẽ sau. Tính giá trị của biểu thức
2
S a b c
.
Câu 4. Một chất điểm chuyển động theo quy luật 3 2
6 9 2
S t t t
với
0
t
(giây) là khoảng thời
gian tính từ lúc vật bắt đầu chuyển động và
S
(mét) là quãng đường vật chuyển động trong thời gian đó,
Mã đề 122 Trang 5/5
trong khoảng thời gian
10
giây, kể từ lúc bắt đầu chuyển động, khoảng
a;b
là khoảng thời gian vận tốc
của vật tăng. Tính
a b
?
Câu 5. Cho hai vị trí
A
,
B
cách nhau
615
m
, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách
từ
A
và từ
B
đến bờ sông lần lượt là
118
m
và
487
m
. Một người đi từ
A
đến bờ sông để lấy nước
mang về
B
. Đoạn đường ngắn nhất mà người đó có thể đi là bao nhiêu mét (làm tròn đến hàng đơn vị)
Câu 6. Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho toạ độ
của hạt (đơn vị: mét) tại thời điểm
t
giây là 3
12 3, 0
y t t t
. Tìm quãng đường hạt đi được trong
khoảng thời gian
0 3
t
.
------ HẾT ------