Mã đề 111 Trang 1/3
S
Ở
GDĐT KON TUM
KI
Ể
M TRA CU
I K
Ỳ
I
TRƯỜNG THCS VÀ THPT
LIÊN VIỆT KON TUM
ĐỀ CHÍNH THỨC
(Đề gồm có 03 trang)
NĂM HỌC 2024 – 2025
Môn: Toán; Lớp 11
Thời gian làm bài:90 phút, không kể thời gian phát đề.
Họ và tên: ........................................................................ Số báo danh: .......
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chọn một phương án.
Câu 1. Nếu lim n
nu a
 và lim n
nv
  thì lim n
nn
u
v
 bằng
A.  . B.  . C. 1. D. 0.
Câu 2. Cho dãy số
,
n
u biết
2
2
2 1.
3
n
n
un
Tìm số hạng 5.u
A. 5
7.
4
u B. 5
17 .
12
u C. 5
71.
39
u D. 5
1.
4
u
Câu 3. Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép
nhóm sau:
Giá trị đại diện của nhóm
30;40 là
A. 35. B. 30 . C. 40 . D. 9.
Câu 4. Cho cấp số cộng ( )
n
u với 13u và 27u. Công sai của cấp số cộng đã cho bằng
A. 4. B. 3
7. C. 7
3. D. 4.
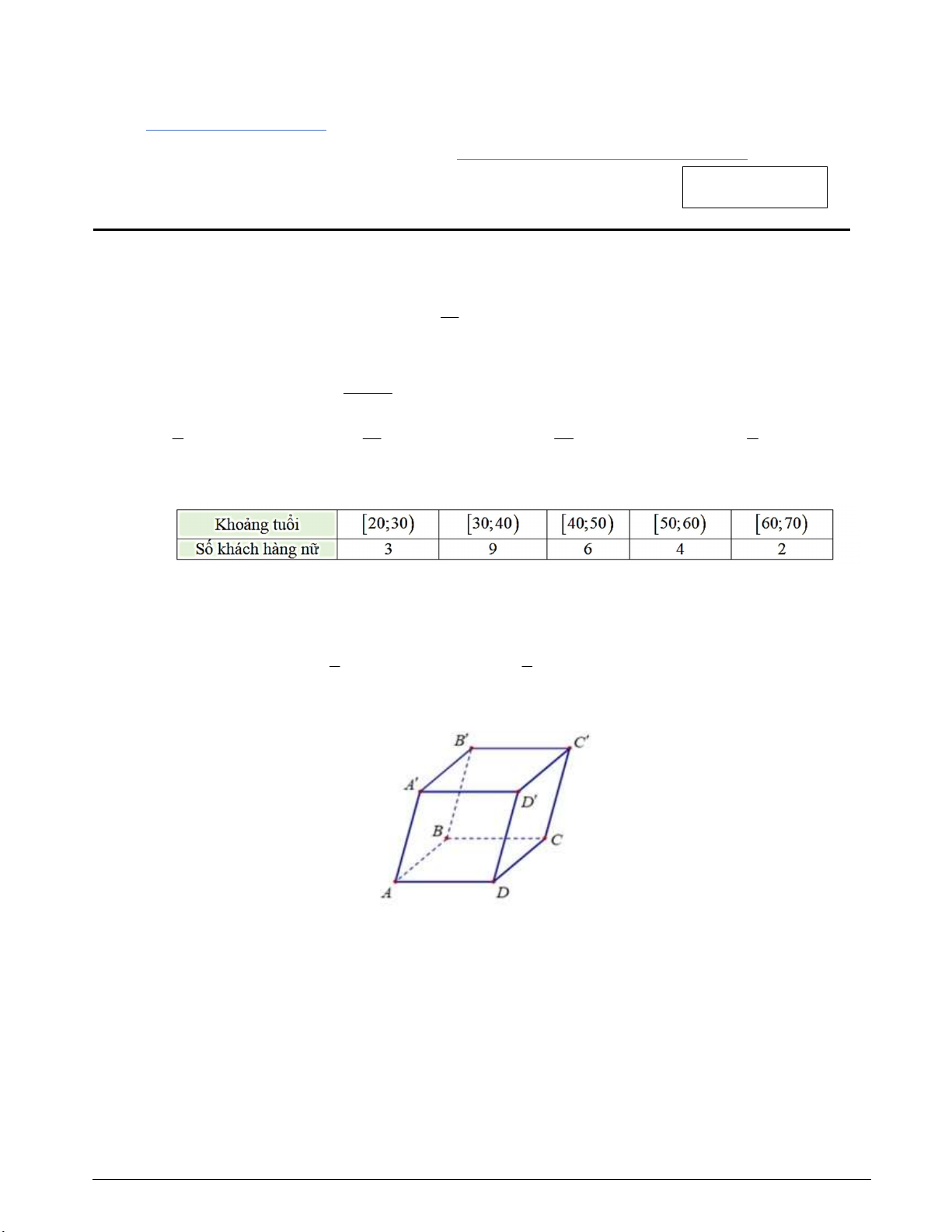
Câu 5. Cho hình hộp . ' ' ' 'ABCD A B C D . Xác định hình chiếu của điểm 'B trên mặt phẳng ABCD theo
phương 'AA .
A. 'A. B. B. C. A. D. .D
Câu 6. Một đường tròn có bán kính 30cm. Tính độ dài của cung tròn trên đường tròn đó có số đo 2,5.
A. 75cm. B. 7,5cm. C. 0,83cm . D. 12cm.
Mã
đ
ề
111
Mã đề 111 Trang 2/3
Câu 7. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
, ,
M N K
lần lượt là trung điểm các
cạnh
, ,
AB BC SB
. Chọn khẳng định đúng trong các khẳng định dưới đây.
A.
/ /
MNK SAC
. B.
/ /
MNK SCD
. C.
/ /
MNK SAB
. D.
/ /
MNK SAD
.
Câu 8. Cho cấp số nhân có các số hạng lần lượt là
3; 9; 27; 81; ...
. Tìm số hạng tổng quát
n
u
của cấp số
nhân đã cho.
A.
1
3 .
n
n
u
B.
3 3 .
n
n
u
C.
3 .
n
n
u
D.
1
3 .
n
n
u
Câu 9. Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Hai đường thẳng cắt nhau
.
B. Bốn điểm phân biệt
.
C. Một điểm và một đường thẳng
.
D. Ba điểm phân biệt
.
Câu 10. Cho tứ diện
ABCD
. Gọi
G
là trọng tâm của tam giác
ABD
,
Q
thuộc cạnh
AB
sao cho
2
AQ QB
,
P
là trung điểm của
CB
. Khẳng định nào sau đây đúng?
A.
//
PQ BCD
. B.
//
GQ BCD
. C.
//
PQ ACD
. D.
Q GDP
.
Câu 11. Cho biết
lim 1
n
nu

. Giá trị của
lim 2 3
n
nu

bằng
A. 1. B. 3. C.
. D.
1
.
Câu 12. Cho tứ diện
ABCD
. Gọi
G
và
E
lần lượt là trọng tâm của tam giác
ABD
và
ABC
. Mệnh đề nào
dưới đây đúng?
A.
GE
và
CD
chéo nhau. B.
GE
cắt
CD
. C.
//
GE CD
. D.
GE
cắt
AD
.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng
hoặc sai.
Câu 1. Cho hàm số sin
4
y x
và
sin
y x
, khi đó
a) Tập giá trị của hàm số
sin
y x
là
[ 1;1]
.
b) Phương trình
sin sin
4
x x
có nghiệm là 3
( )
8
x k k
c) Trên khoảng
(0;2 )
phương trình
sin sin
4
x x
có 3 nghiệm
d) Trên khoảng
(0;2 )
, tổng các nghiệm của phương trình
sin sin
4
x x
bằng
7
4
Câu 2. Người ta đo đường kính của 70 cây gỗ được trồng sau
12
năm (đơn vị: centimet) họ thu được bảng
tần số ghép nhóm sau:
Đường kính cây gỗ (cm)
[20;25)
[25;30)
[30;35)
[35;40)
[40;45)
Số cây gỗ
6
13
28
16
7
a) Cỡ của mẫu số liệu là
70
n
.
b) Giá trị đại diện của nhóm
[35;40)
là 16.
c) Mốt của mẫu số liệu ghép nhóm này là
33,8
.
d)
75%
số cây gỗ trồng sau
12
năm có đường kính ít nhất là
29, 4
cm
K
N
M
C
A
B
D
S
Mã đề 111 Trang 3/3
Câu 3. Cho tứ diện
SABC
. Gọi
M
trên cạnh AB sao cho BM = 3AM và
N
là trung điểm của
BC
.
a) Đường thẳng
MN
nằm trong mặt phẳng
ABC
.
b) Đường thẳng
MN
và đường thẳng
AC
chéo nhau.
c) Giao điểm của đường thẳng
MN
và mặt phẳng
( )
SAC
là giao điểm của
MN
và
AC
.
d) Gọi
P
là trung điểm của
SC
. Khi đó
/ /
NP SAB
.
Câu 4. Cho dãy số
n
u
:
2 1
3 2
n
n
u
n
, dãy
n
v
có
lim 9
n
nv

a)
2
lim
3
n
nu

.
b)
25
lim ( )
3
n n
nu v

c)
lim (2 u ) 3
n
n
.
d)
lim ( 3 ) 0
n
nv a

. Khi đó
3
a
.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho
2
2
3 5
lim 2
4 10
n
an n
n

. Tính 2a + 7.
Câu 2. Tính tổng 1
2 2 2 2
2 ...
5 25 125 5
n
S
Câu 3. Giá của một chiếc xe ô tô lúc mới mua là 600 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô
tô giảm 50 triệu đồng. Tính giá còn lại của chiếc xe sau
5
năm sử dụng là bao nhiêu triệu đồng.
Câu 4. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
M
là trung điểm của
.
SC
Gọi
I
là
giao điểm của
AM
với mặt phẳng
.
SBD
Khi đó
AM k IM
. Tìm giá trị của
3
k
.
Câu 5. Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
G
là trọng tâm của tam giác
ABC
và
E
là điểm thuộc cạnh
SA
thỏa mãn
AE a
AS b
với
a
b
là phân số tối giản. Biết rằng
GE
song song với mặt
phẳng
SCD
. Tìm giá trị của
2 3
a b
.
Câu 6. Cho tứ diện
ABCD
, biết tam giác
BCD
đều cạnh
4 3
. Gọi M là trung điểm của AB. Mặt phẳng
P
đi qua điểm M và song song với mặt phẳng
BCD
cắt các mặt còn lại của tứ diện theo một đa giác có
diện tích bằng
3
a
. Tìm giá trị của 2a + 1.
------ HẾT ------