Mã đề 121 Trang 1/4
S
Ở
GDĐT KON TUM
KI
Ể
M TRA CU
I K
Ỳ
I
TRƯỜNG THCS VÀ THPT
LIÊN VIỆT KON TUM
ĐỀ CHÍNH THỨC
(Đề gồm có 04 trang)
NĂM HỌC 2024 – 2025
Môn: TOÁN; Lớp 12
Thời gian làm bài: 90 phút, không kể thời gian phát đề.
H
ọ
và tên:
............................................................................
S
ố
báo danh: .......
PHẦN I. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
Câu 1. Trong không gian Oxyz , cho 3u i k
. Tọa độ của vectơ u
là
A.
1;0; 3. B.
1; 3;0. C.
1; 1;3. D.
0;2; 3.
Câu 2. Trong không gian Oxyz , cho
1; 3; 6a
và
3; 2; 1b
. Tọa độ của a b
là
A. (4; 5; 7). B. (3; 6; 6) . C. (2; 1; 5). D. (4; 6; 7).
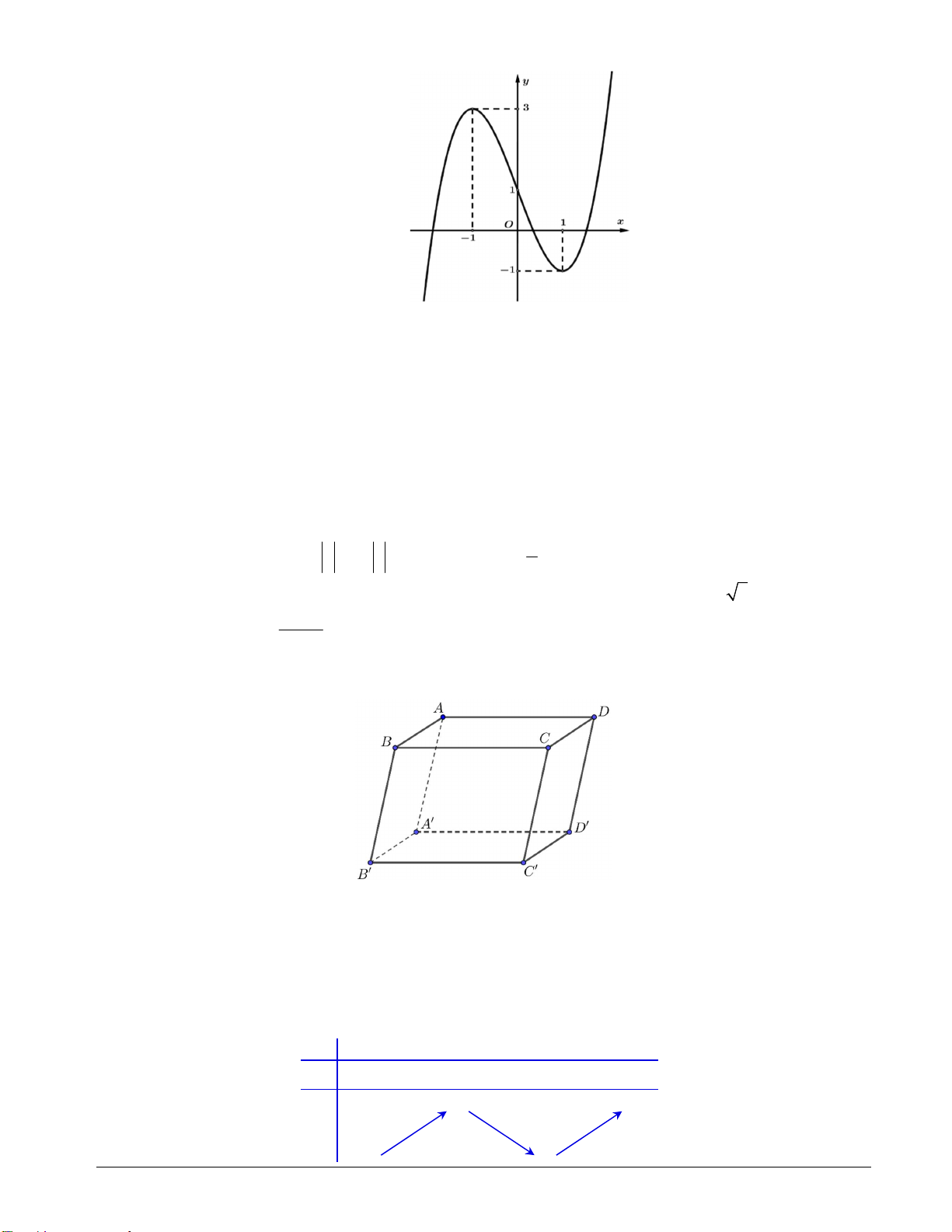
Câu 3. Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A.
22 3
2
x x
yx
. B.
22 2
1
x x
yx
. C.
23
2
x x
yx
. D. 2 2
1
x
yx
.
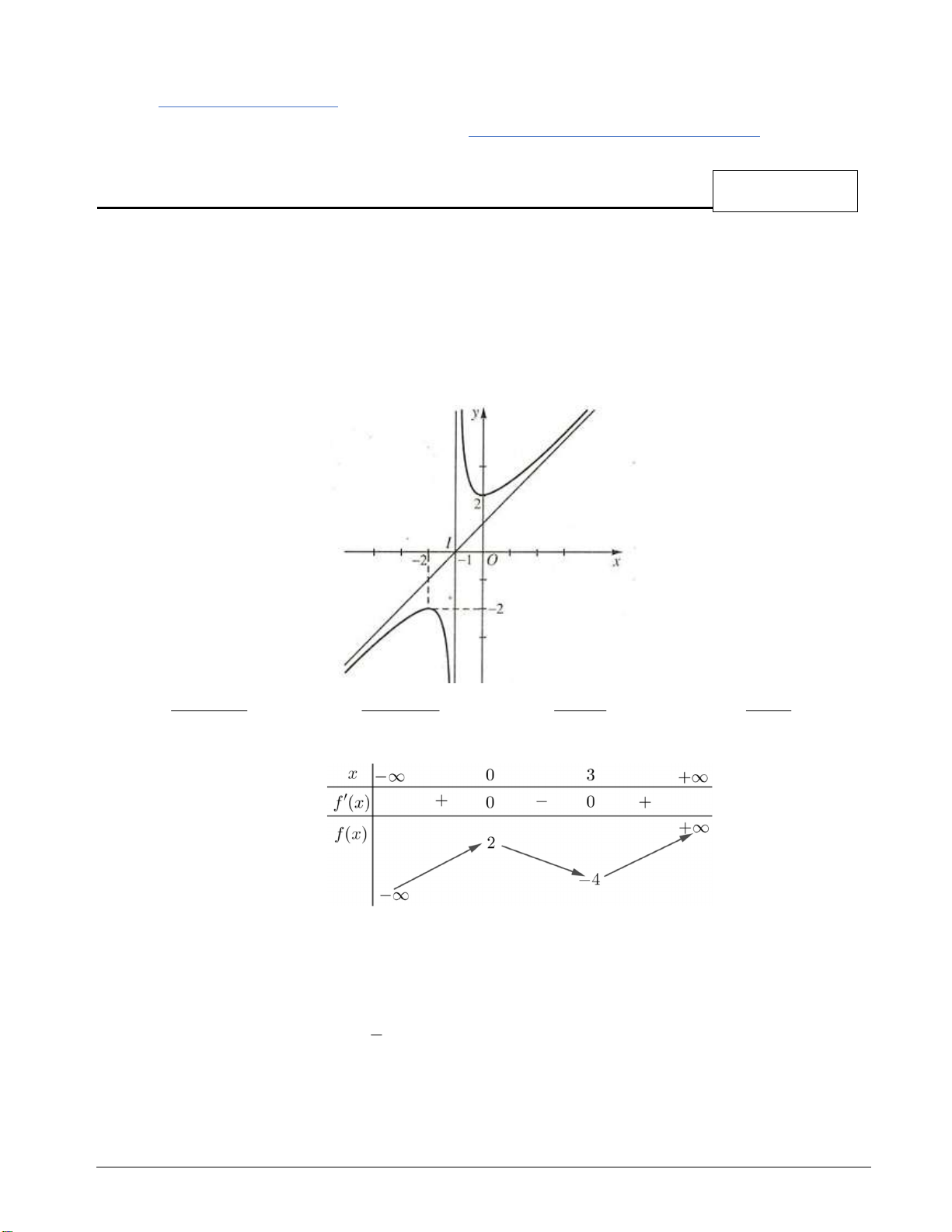
Câu 4. Cho hàm số
f x có bảng xét dấu của đạo hàm như sau
Hàm số
y f x nghịch biến trên khoảng nào dưới đây?
A. (0; 3) . B. ( ; 0) . C. (0; ) . D. ( 4; 2)
Câu 5. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC với
1;3;4 , 2; 1;0 , 3;1; 2A B C. Tọa
độ trọng tâm G của tam giác ABC là
A.
6;3;6G. B. 2
3; ;3
3
G
. C.
2;1;2G. D.
2; 1; 2G.
Mã
đ
ề
121
Mã đề 121 Trang 2/4
Câu 6. Cho hàm số
y f x có đồ thị như hình vẽ dưới đây.
Hàm số
y f x đạt cực đại tại điểm
A. 3x. B. 0x. C. 1x. D. 1x .
Câu 7. Giá trị nhỏ nhất của hàm số 32y x x trên đoạn
1;1 bằng
A. 1. B. 3. C. 0. D. 3.
Câu 8. Trong không gian Oxyz , cho 3 điểm
1;2; 1A,
2; 1;3B,
3;5;1C. Tọa độ điểm D sao cho tứ
giác ABCD là hình bình hành là
A.
2;2;5. B.
4;8; 3 . C.
2;8; 3 . D.
4;8; 5 .
Câu 9. Cho tứ diện ABCD. Khẳng định nào sau đây là đúng?
A. AB AD BD
. B. AB BC AD

. C. AB BC AC

. D. AB BC CA
.
Câu 10. Cho hai vectơ ,u v
có 2, 3u v
và
1
cos , 2
u v
. Khi đó, .u v
bằng
A. 3. B. 6. C. 12. D. 3 3 .
Câu 11. Cho hàm số 4 1
2 6
x
yx
. Đường tiệm cận ngang của đồ thị hàm số là
A. 2y. B. 4y. C. 3x. D. 3x .
Câu 12. Cho hình hộp chữ nhật .ABCD A B C D
.
Vectơ AD
bằng với vectơ nào sau đây?
A. B C
. B.
D A

. C. CB
. D. AA
.
PHẦN II. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng
hoặc sai.
Câu 1. Cho hàm số đa thức bậc ba
y f x xác định trên
và có bảng biến thiên như hình dưới đây.
x
–
∞
-
1
3
+
∞
y'
+
0
–
0
+
y
–
∞
4
-
2
+
∞
Mã đề 121 Trang 3/4
a) Hàm số đã cho nghịch biến trên khoảng
1;3.
b) Điểm cực tiểu của hàm số đã cho là 3.
c) Giá trị (0)f nhỏ hơn giá trị (2)f
d) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
y f x tạo với hai trục toạ độ một tam giác có
diện tích lớn hơn 2.
Câu 2. Cho hàm số ax b
yx c
( , , .a b c
) có đồ thị như hình dưới.
a) Đường thẳng 1x là đường tiệm cận đứng của đồ thị hàm số.
b) Hàm số đồng biến trên từng khoảng xác định của nó.
c) Hàm số đạt giá trị nhỏ nhất bằng 2 trên đoạn
2;0.
d) Giá trị của a c bằng 0.
Câu 3. Cho hình lập phương .ABCD A B C D
có các cạnh bằng a. Gọi O là giao điểm của AC và BD.
a) Hai vectơ OB
và B D
là hai vectơ ngược hướng.
b) 2B D DO
.
c) Góc giữa hai vectơ A C
và AD
là 45.
d) 2
2
.2
A D AC a
.
Câu 4. Trong không gian Oxyz , cho các điểm
1;0;0 , 3;2;4 , 0;5;4A B C .
a) Vectơ AB
có tọa độ là
2; 2; 4 .
b) Toạ độ trung điểm của đoạn thẳng AB là
2;1;2 .
Mã đề 121 Trang 4/4
c)
1
cos 5
ABC .
d) Xét điểm M thuộc mặt phẳng
Oxy sao cho 2MA MB MC
 
đạt giá trị nhỏ nhất, khi đó tọa độ điểm
1;3;0M.
PHẦN III. Học sinh trả lời từ câu 1 đến câu 6.
Câu 1. Trong không gian Oxyz , cho hình bình hành ABCD với
1 2 3; ;A,
2 5 4; ;B,
0 2 0; ;C. Gọi
; ;D a b c . Tính a b c .
Câu 2. Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một
chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm
800;500;7A đến điểm
940;550;9B
trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp
theo là ( ; ; )C x y z . Tính x y z .
Câu 3. Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là
hình vuông và diện tích bề mặt bằng 108 cm2 như hình dưới đây.
Biết khi 0 0
(cm), ( )x x h h cm thì thể tích của hộp là lớn nhất. Khi đó 0 0
x h bằng bao nhiêu?
Câu 4. Một công ty ước tính rằng chi phí C(USD) để sản xuất xđơn vị sản phẩm có thể được mô hình hóa
bằng công thức 2
( ) 0,00025 0,04 1000C x x x . Tìm mức sản xuất x sao cho chi phí trung bình
( )
( ) C x
C x x
cho mỗi đơn vị hàng hóa là nhỏ nhất.
Câu 5. Cho tứ diện ABCD có , ,AB AC AD đôi một vuông góc và có độ dài đều bằng 4. Gọi ,M N lần lượt
thuộc cạnh AB , CD sao cho 1
4
AM AB, 1
4
CN CD. Tính tích vô hướng .MN AD
.
Câu 6. Một chiếc điện thoại iphone được đặt trên một giá đỡ có ba chân với điểm đặt
0;0;20S và các điểm
chạm mặt đất của ba chân lần lượt là
0; 6;0 , 3 3;3;0A B,
3 3;3;0C (đơn vị cm). Cho biết điện
thoại có trọng lượng là 2 N và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 1 2 3
, ,F F F
có độ
lớn bằng nhau. Biết tọa độ của lực
1; ;F a b c
, khi đó 2 5 30a bT c bằng?
------ HẾT ------
F
3
F
2
F
1
z
y
x
C
O
A
B
S