Đề thi học kì 1 môn Toán lớp 8 năm 2023-2024 có đáp án - Trường THCS Võ Trường Toản, Châu Đức

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

14
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Việc ôn tập và hệ thống kiến thức với ‘Đề thi học kì 1 môn Toán lớp 8 năm 2023-2024 có đáp án - Trường THCS Võ Trường Toản, Châu Đức’ được chia sẻ dưới đây sẽ giúp bạn nắm vững các phương pháp giải bài tập hiệu quả và rèn luyện kỹ năng giải đề thi nhanh và chính xác để chuẩn bị tốt nhất cho kì thi sắp diễn ra. Cùng tham khảo và tải về đề thi này ngay bạn nhé!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học kì 1 môn Toán lớp 8 năm 2023-2024 có đáp án - Trường THCS Võ Trường Toản, Châu Đức

TRƯỜNG THCS VÕ TRƯỜNG TOẢN ĐỀ KIỂM TRA CUỐI HỌC KỲ I TỔ KHOA HỌC TỰ NHIÊN NĂM HỌC: 2023 – 2024 ĐỀ CHÍNH THỨC MÔN: TOÁN – KHỐI: 8 Thời gian làm bài: 90 phút I. TRẮC NGHIỆM (3,0 ĐIỂM) Chọn đáp án đúng rồi ghi vào giấy Câu 1: Trong các biểu thức đại số sau, Biểu thức đơn thức là 1 1 A. x3 y . B. x  y . C. xy 2  1 . D. 1- 3xy. z 2 Câu 2: Kết quả của phép tính 2 x.( x  y) là A. 2 x2  2 xy . B. x2  2 xy . C. 2 x  2 xy . D. 2x 2  y . 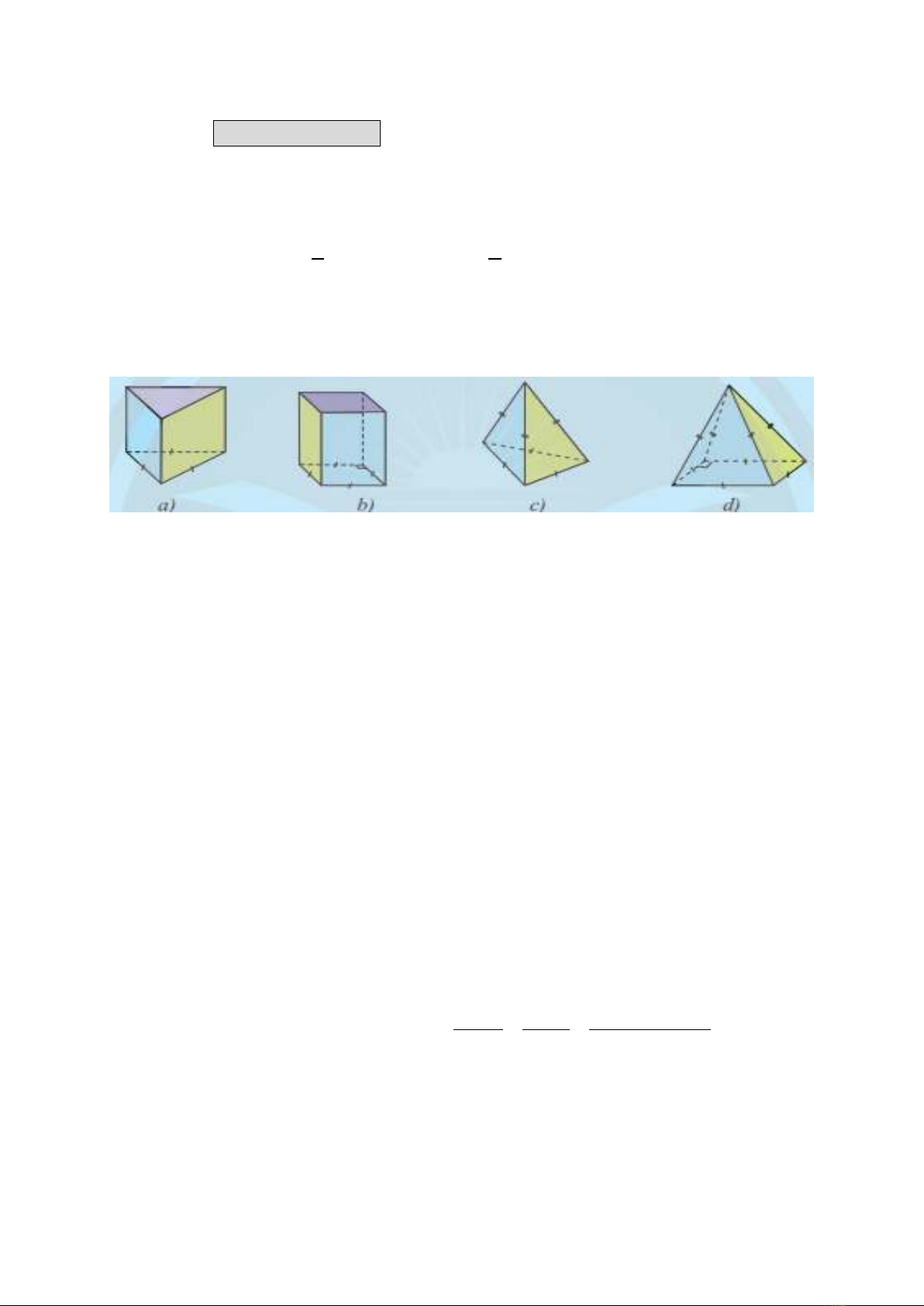Câu 3: Hình chóp tứ giác đều là A. hình a. B. hình b. C. hình c. D. hình d. Câu 4: Khi biểu diễn tỉ lệ phần trăm học lực cuối học kì. Ta nên lựa chọn A. biểu đồ tranh. B. biểu đồ cột kép. C. biểu đồ đoạn thẳng. D. biểu đồ hình quạt tròn. Câu 5: Bậc của đa thức N = x3 +2x2y2 + 3 là A. 3. B. 4. C. 1. D. 2. Câu 6: Cho hình thang cân ABCD (AB // CD) có Aˆ  75o . Số đo góc C là A. Cˆ  75o . B. Cˆ  105o . C. Cˆ  95o . D. Cˆ  115o . II. PHẦN TỰ LUẬN (7,0 ĐIỂM) Câu 7: (1,0 điểm) Thực hiện tính. a/ -9x3y2 : 3x3y b/ x2y + 3xy2 – (4xy2 + x2y) Câu 8: (1,0 điểm) Phân tích đa thức thành nhân tử. a/ x3 – 16x b/ x2 + 1 – y2 + 2x 2 3 6x  5 Câu 9: (1,0 điểm) Cho biểu thức: A =   2 x  3 2 x  1 (2 x  3)(2 x  1) a/ Tìm điều kiện xác định của A b/ Thu gọn A
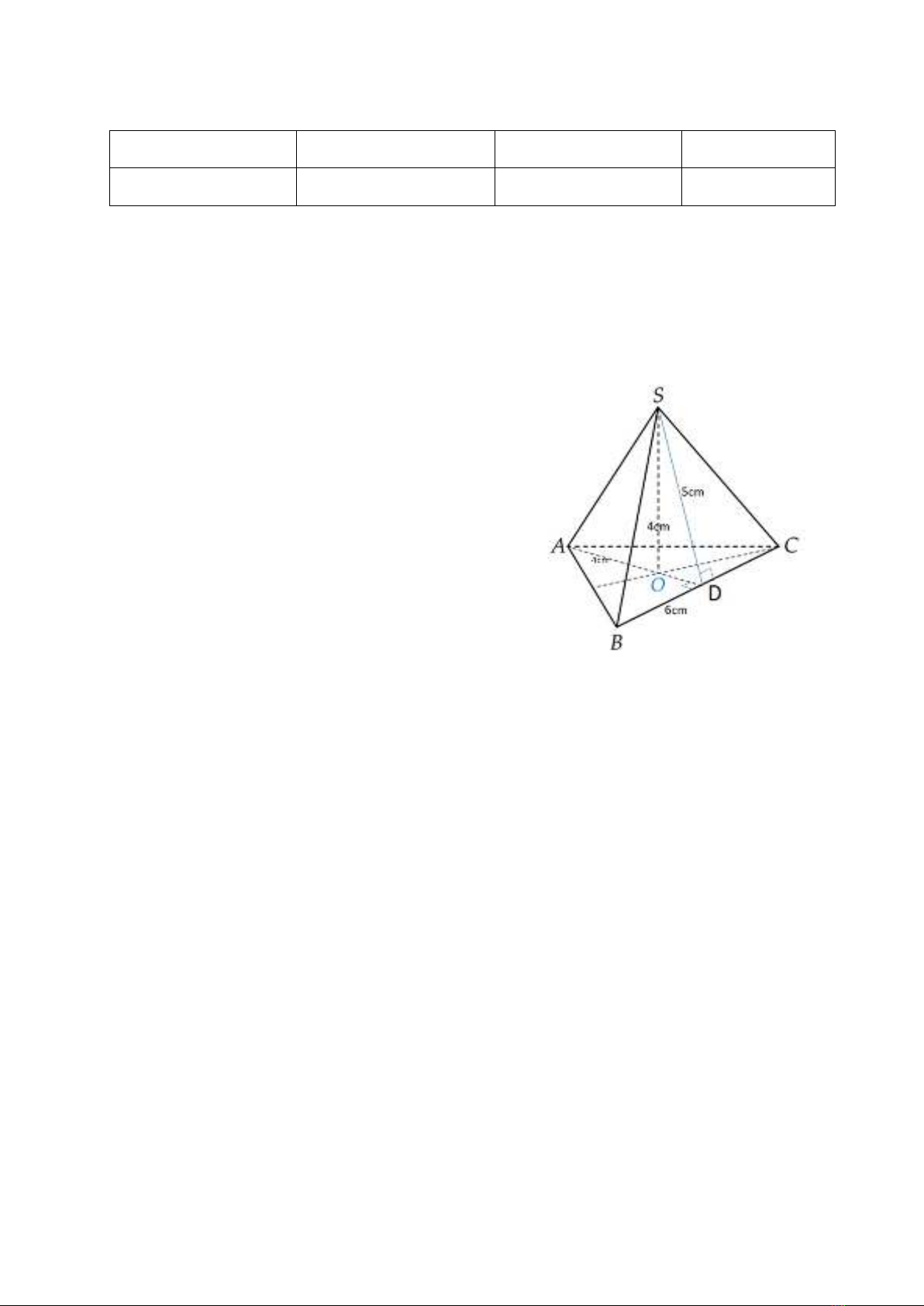
Câu 10: (1,0 điểm) Xếp loại học lực lớp 8A được thống kê trong bảng sau Tốt Khá Đạt Chưa đạt 5 10 23 2 a/ Tính tỉ lệ phần trăm các loại học lực của lớp 8A. b/ Chọn biểu đồ thích hợp rồi vẽ biểu đồ biểu diễn tỉ lệ phần trăm các loại học lực của lớp 8A. Câu 11: (1,0 điểm) Cho hình chóp tam giác đều S.ABC như hình vẽ (SD = 5cm; SO = 4cm; BC= 6cm; AD = 4cm) a/ Tính diện tích xung quanh hình chóp tam giác đều S.ABC b/ Tính thể hình chóp tam giác đều S.ABC Câu 12: (1,5 điểm) Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm, AM là trung tuyến. a/ Vẽ hình. b/ Tính độ dài BC. c/ Gọi I là trung điểm của AC, trên tia MI lấy điểm K sao cho IK = IM. Chứng minh rằng tứ giác AKCM là hình thoi. Câu 13: (0,5 điểm) Tìm giá trị nhỏ nhất của P = 2x2 + 2x +3.
HƯỚNG DẪN CHẤM CUỐI HỌC KÌ I MÔN TOÁN 8 NĂM HỌC 2023-2024 PHẦN TRẮC NGHIỆM (3,0 ĐIỂM) 1 2 3 4 5 6 A A D D B B PHẦN TỰ LUẬN (7,0 ĐIỂM) Câu Đáp án Điểm Câu 7 : (1,0 điểm) Thực hiện phép tính: A -9x3y2 : 3x3y = -3y 0,5 x2y + 3xy2 – (4xy2 + x2y) = x2y + 3xy2 – 4xy2 - x2y b 0,25 +0,25 2 2 2 2 2 = (x y - x y )+( 3xy – 4xy ) = - xy Câu 8 :(1,0đ) Phân tích đa thức thành nhân tử a x3 - 6x = x(x2 – 16) = x(x+4)(x-4) 0,25 + 0,25 x2 + 1 – y2 + 2x = (x2 + 2x + 1) - y2 = (x+ 1)2 – y2 0,25 b 0,25 = (x+1+ y)(x+1- y) 2 3 6x  5 Câu 9: ( 1,0 điểm). Cho biểu thức: A =   2 x  3 2 x  1 (2 x  3)(2 x  1) 3 1 a x ;x  2,25 + 0,25 2 2 2 3 6x  5   2 x  3 2 x  1 (2 x  3)(2 x  1) 2(2 x  1) 3(2 x  3) 6x  5    0,25 (2 x  3)(2 x  1) (2 x  3)(2 x  1) (2 x  3)(2 x  1) 4x  2  6x  9  6x  5 b  (2 x  3)(2 x  1) 4x  6 2(2 x  3)   (2 x  3)(2 x  1) (2 x  3)(2 x  1) 2  0,25 2x  1 Câu 10: (1,0 điểm) Xếp loại học lực lớp 8A được thống kê trong bảng sau a Tính tỉ lệ phần trăm đúng 0,5 b Chọn được biểu đồ vẽ được biểu đồ đúng 0,25 + 0,25 Câu 11: (1,0 điểm) Cho hình chóp tam giác đều S.ABC như hình vẽ (SD = 5cm; SO = 4cm; BC= 6cm; AD = 4cm)
1 a Sxq 3.SM .bên 3. .6.5 45 cm2 0,5 2 1 1 1 b V S .h . .6.4 .4 16 cm3 0,5 3 day 3 2 Câu 12: (1,5 điểm) Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm, AM là trung tuyến. a Vẽ hình đúng 0,5 b Áp dụng định lý Pythagore tính đúng BC = 10cm 0,5 Chứng minh được AMCK là hình bình hành 0.25 c Chứng minh được AM = MC và kết luận AMCK là hình thoi. 0.25 Câu 13: (0,5 điểm) Tìm giá trị nhỏ nhất của P = 2x2 + 2x +3. 3 P  2 x2  2 x  3  x2  x  2  1 1 3 1   x 2  2 x.      2 4 2 4 0,25 2  1 5 5 x     2 4 4 5 1 Pmin  khi x   0,25 4 2 Ghi chú: Học sinh giải cách khác đúng cho đủ điểm theo từng phần. ____HẾT____