UBND QUẬN BÌNH THẠNH
TRƯỜNG THCS RẠNG ĐÔNG
ĐỀ THAM KHẢO CUỐI HỌC KÌ II
Năm học 2024 – 2025
Môn Toán – Lớp 8
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (3,0 ĐIỂM)
Em hãy chọn phương án đúng trong mỗi câu dưới đây:
Câu 1. Hệ số góc của đường thẳng y = -2x + 2024 là:
A. 2 B. - 2 C. – 2024 D. 2024
Câu 2. Cho hai đường thẳng (d): y = 5x – 2 và (d’): y = 3x – 2. Khi đó hai đường thẳng (d)
và (d’):
A. cắt nhau B. song song C. vuông góc D. trùng nhau
Câu 3. Trong các hàm số sau hàm số nào là hàm số bậc nhất:
A. y = 4x - 5 B. y = 0 C. y = √𝑥𝑥 D. y = 𝑥𝑥2−3
Câu 4. Phương trình nào sau đây là phương trình bậc nhất một ẩn?
A.
0 2023 2024x+=
B.
5 70x−=
C.
34 1xy+=−
D.
2
2 30x+=
Câu 5.
=1x
là nghiệm của phương trình nào sau đây.
A.
+=2 30x
B.
+=2 20x
C. 3
D.
+=10x
Câu 6. Xe thứ hai đi chậm hơn xe thứ nhất 15km/h. Nếu gọi vận tốc xe thứ hai là x (km/h)
thì vận tốc xe thứ nhất là:
A. x – 15 (km/h) B. 15x (km/h) C. x + 15(km/h) D. 15 – x (km/h)
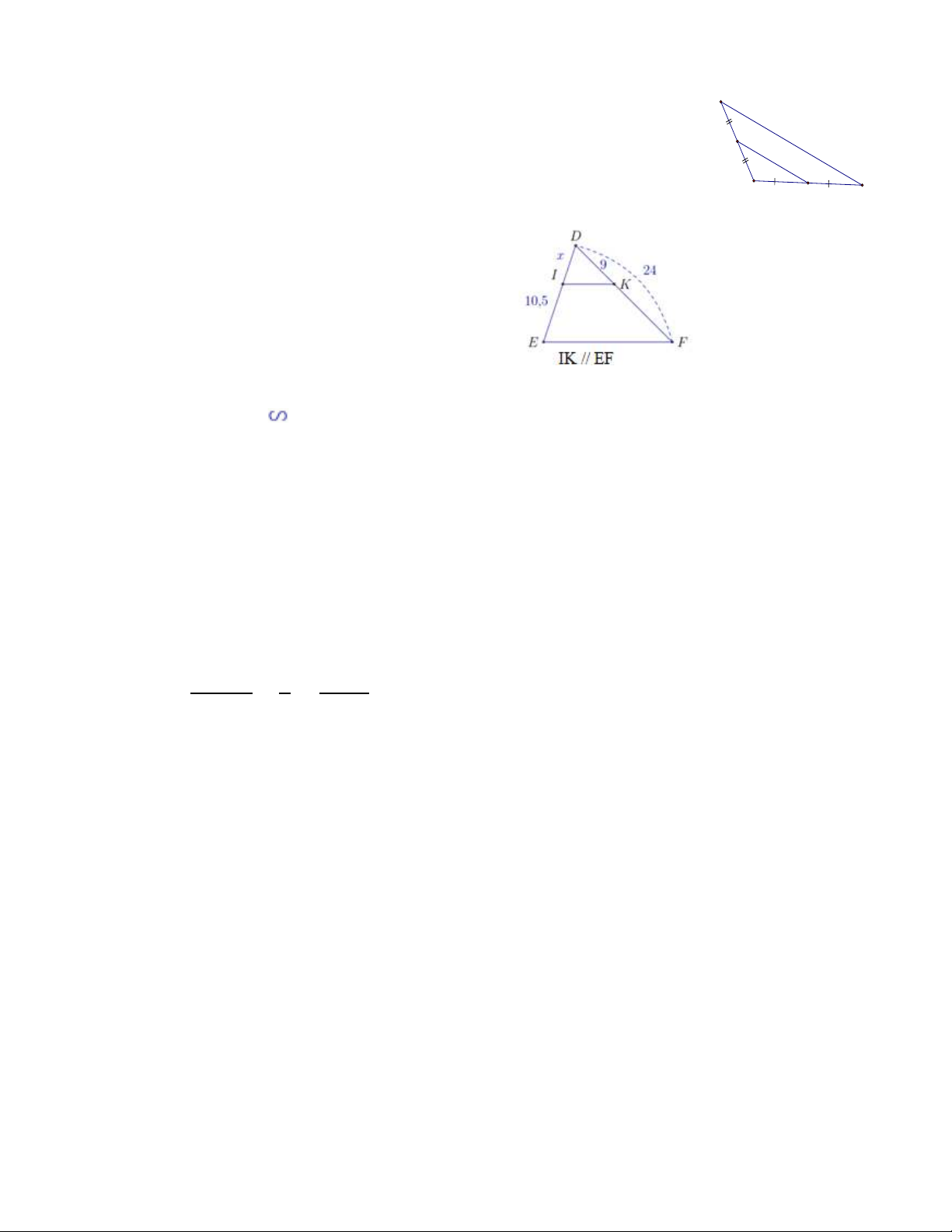
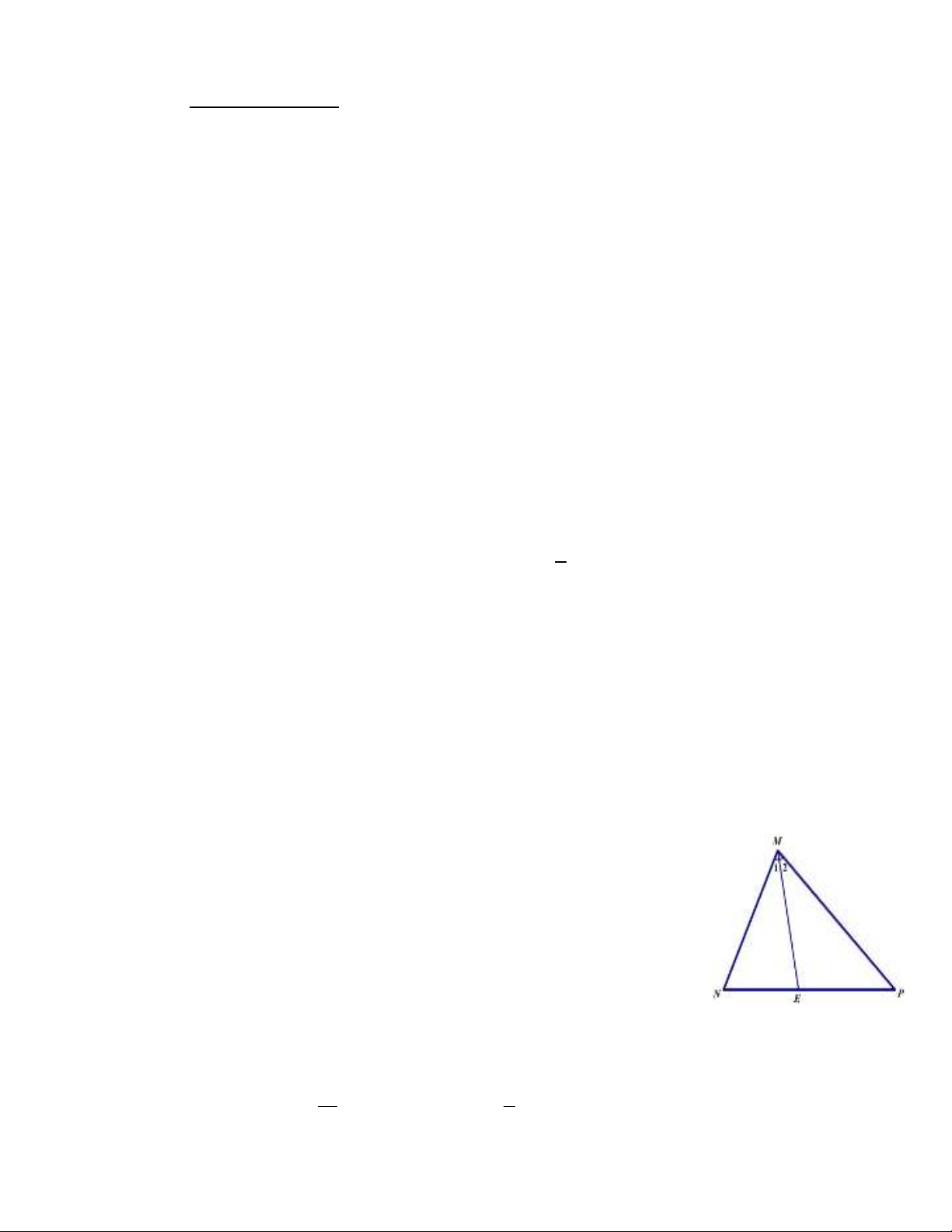
Câu 7. Cho hình vẽ biết 𝑀𝑀1
�=𝑀𝑀2
�. Khẳng định nào sau đây là đúng ?
A.ME là đường phân giác của tam giác MNP
B.ME là đường trung bình của tam giác MNP
C.ME là đường trung tuyến của tam giác MNP
D.ME là đường cao của tam giác MNP
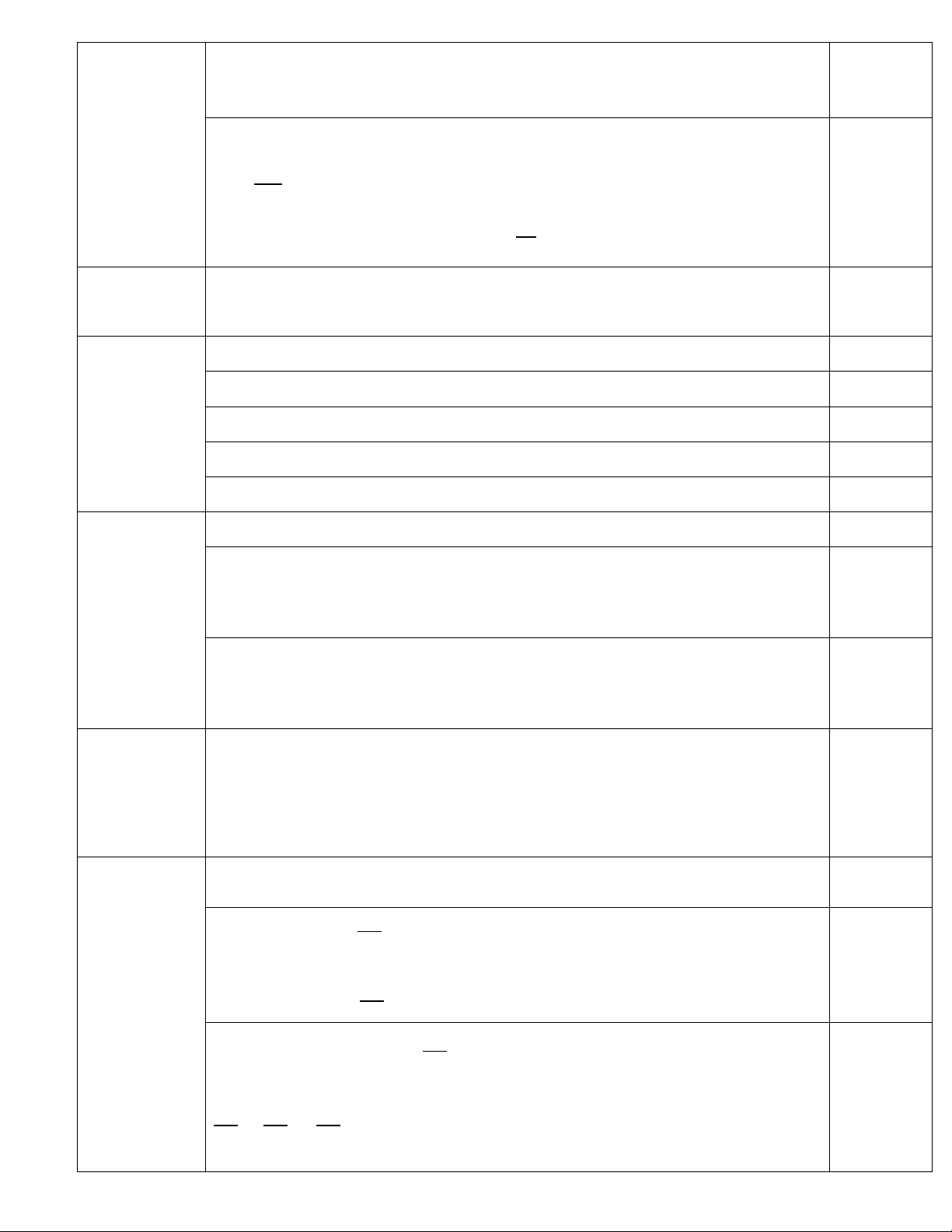
Câu 8. Nếu
ABC∆
đồng dạng
MNP∆
theo tỉ số đồng dạng k = 5 thì
MNP∆
đồng dạng
ABC∆
theo tỉ số đồng dạng là:
A.5 B.
1
10
C.
1
5
D.10
Câu 9. Tìm x trong hình vẽ bên, biết D, E lần lượt là trung điểm của AB, AC và DE = 6
cm.
A. x = 6 cm. B. x = 12 cm.
C. x = 3 cm. D. x = 2 cm.
Câu 10. Tính x trong các trường hợp sau
A. 6,1
B. 6,2
C. 6,3
D. 6.4
Câu 11. Cho ∆KFC ∆MNP và 𝐾𝐾
�= 30°; 𝑃𝑃
�= 80° ;số đo 𝑁𝑁
�=? :
A. 𝑁𝑁
�= 60° B. 𝑁𝑁
�= 70° C. 𝑁𝑁
�= 80° D. 𝑁𝑁
�= 90°
Câu 12: Một tam giác có thể vẽ tối đa mấy đường trung bình?
A. 1 B. 2 C. 4 D. 3
II. PHẦN TỰ LUẬN (7,0 ĐIỂM)
Câu 1: (1,25 điểm). Giải các phương trình sau :
𝑎𝑎) 6𝑥𝑥 − 5 = 8𝑥𝑥+ 9
𝑏𝑏) 2𝑥𝑥 − 1
2+1
3=𝑥𝑥 − 2
4
Câu 2: (1,5 điểm ). Cho hai đường thẳng (d): y = -3x và (d’): y = 2x + 5
a) Vẽ hai đường thẳng (d) và (d’) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
Câu 3: (1,0 điểm ). Một người đi xe máy từ A đến B với vận tốc 60km/h, rồi đi từ B quay
về A với vận tốc lúc đi 45km/h. Biết rằng thời gian cả đi lẫn về là 4 giờ 40 phút. Tính độ
dài quãng đường AB?
Câu 4: (2,5 điểm). Cho ∆ABC vuông tại A, đường cao AH.
a) Chứng minh
ABC HBA∆∆∽
và viết tỉ số đồng dạng
b) Chứng minh
2
AH HB.HC=
c) Phân giác của góc ABC cắt AH và AC lần lượt tại I và K. Chứng minh
2
AI IH.KC=
x
6 cm
D
E
B
A
C
Câu 5: (0,75 điểm). Nhìn vào hình vẽ dưới đây
(đơn vị tính trong hình là mét). Em hãy tính
xem bề rộng PQ của hồ là bao nhiêu mét? (cho
biết QR // ST)
---HẾT---
ĐÁP ÁN ĐỀ THAM KHẢO CUỐI HỌC KÌ II NĂM HỌC 2024 – 2025
MÔN TOÁN LỚP 8
Phần I: Trắc nghiệm (3đ): Mỗi câu trả lời đúng 0,25 đ
1
2
3
4
5
6
7
8
9
10
11
12
B
A
A
B
C
C
A
C
B
C
B
D
Phần II: Tự luận (7đ)
Hướng dẫn chấm
Điểm
Câu 1:
(1,25 điểm)
Gi
ải các phương trình sau :
a)
6𝑥𝑥 − 5 = 8𝑥𝑥+ 9
6x – 8x = 9 + 5
0,25
−2𝑥𝑥= 14
x = -7
Vậy phương trình có nghiệm x = -7
0,25
b)
2𝑥𝑥 − 1
2+
1
3=
𝑥𝑥 − 2
4
6( 2x – 1) + 1. 4 = 3(x - 2 )
0,25
100
150
100
R
S
P
T
Q
12x – 6 + 4 = 3x -6
12x – 3x = - 6 + 6 - 4 0,25
9x = -4
𝑥𝑥=−4
9
Vậy phương trình có nghiệm 𝑥𝑥=−4
9
0,25
Câu 2:
( 1,5 điểm )
Cho hai đường thẳng (d): y = -3x và (d’): y = 2x + 5
a)
Vẽ hai đường thẳng (d) và (d’) trên cùng một mặt phẳng tọa độ Oxy.
Đúng bảng giá trị của (d)
0,25
Vẽ đúng (d)
0,25
Đúng bảng giá trị của (d’)
0,25
Vẽ đúng (d’)
0,25
b)
Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
Phương trình hoành độ giao điểm của (d) và (d’) :
-3x = 2x + 5
x = -1 0,25
Thay x = -1 vào (d) : y = -3x, ta được:
y = -3.-1=3
Vậy tọa độ giao điểm của của (d) và (d’) là ( -1 ; 3 ) 0,25
Câu 3:
( 1 điểm )
Một người đi xe máy từ A đến B với vận tốc 60km/h, rồi đi từ B
quay về A với vận tốc lúc đi 45km/h. Biết rằng thời gian cả đi lẫn về
là 4 giờ 40 phút. Tính độ dài quãng đường AB?
Gọi x (km) là chiều dài quãng đường AB (x > 0)
0,25
𝑇𝑇ℎờ𝑖𝑖 𝑔𝑔𝑖𝑖𝑎𝑎𝑔𝑔 đ𝑖𝑖 ∶
𝑥𝑥
60 𝑔𝑔𝑖𝑖ờ
𝑇𝑇ℎờ𝑖𝑖 𝑔𝑔𝑖𝑖𝑎𝑎𝑔𝑔 𝑣𝑣ề ∶ 𝑥𝑥
45
𝑔𝑔𝑖𝑖ờ
0,25
Đổ𝑖𝑖 ∶ 4 giờ 40 phút =
14
3 giờ
Vì thời gian cả đi lẫn về mất 4 giờ 40 phút nên ta có pt sau :
𝑥𝑥
60 +𝑥𝑥
45 =14
3
0,25
x = 120 ( nhận )
Vậy chiều dài quãng đường AB là 120 km
0,25
Câu 4 :
(2,5 điểm )
a)
Chứng minh : ∆ABC ∆HBA.
Xét ∆ABC và ∆HBA có :
𝐵𝐵𝐵𝐵𝐵𝐵
�=𝐵𝐵𝐵𝐵𝐵𝐵
�= 900
0,25
𝐵𝐵
� là góc chung
0,25
⇒
∆ABC ∆HBA (g.g)
0,25
⟹𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵
=𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵
=𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵
( 𝑡𝑡𝑡𝑡đ𝑑𝑑 ) 0,25
b)
Chứng minh : 𝑨𝑨𝑨𝑨𝟐𝟐=𝑨𝑨𝑯𝑯.𝑨𝑨𝑯𝑯
Chứng minh ∆HBA và ∆HAC
0,5
⟹𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵 =𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵 ( 𝑡𝑡𝑡𝑡đ𝑑𝑑 )
⟹𝐵𝐵𝐵𝐵
2
=𝐵𝐵𝐵𝐵.𝐵𝐵𝐵𝐵
0,25
c)
Chứng minh
2
AI IH.KC=
Chứng minh : AI = AK 0,25
Ta có:
AI BA
IH BH
=
(tính chất phân giác)
KC KC BC
AI KA BA
= =
(tính chất phân giác)
0,25
Mà
( )
AB BC ABC HBA
BH BA
=∆∆∽
2
AI KC AI IH.KC
IH AI
⇒= ⇒ =
0,25