SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ
LỚP 12 THPT NĂM HỌC 2022 - 2023
Môn thi: TOÁN
Ngày thi: 28 tháng 9 năm 2022
Th
ời gian l
àm bài:
180 phút
Câu I (4 điểm)
Cho hàm số 3
3 1
y x x
có đồ thị
C
1) Viết phương trình tiếp tuyến của
( )
C
biết tiếp tuyến đi qua điểm
(2;3).
M
2) Tìm tất cả giá trị của
a
để qua điểm
; 1
A a kẻ được ba tiếp tuyến đến đồ thị
( )
C
trong đó có hai tiếp tuyến vuông góc với nhau.
Câu II (5 điểm)
1) Giải phương trình 2 2
1 2 2 2 1.
x x x x
2) Giải hệ phương trình
3 2
2
3 4 2 1
.
2 3 9 6
x x x y y
y x y y
Câu III (2 điểm)
Gọi
A
là tập hợp các số tự nhiên có
8
chữ số được lập từ các chữ số
1,2,3,4,5,6
sao
cho các chữ số
1
và
2
xuất hiện hai lần, các chữ số còn lại xuất hiện một lần. Chọn ngẫu
nhiên một số thuộc
.
A
Tính xác suất để số được chọn có các chữ số giống nhau không đứng
cạnh nhau.
Câu IV (3 điểm)
Cho dãy số
n
u
xác định bởi 3 2
1 1
2; 2 2 ;
n n n n
u u u u u
1,2,3,...
n
1) Chứng minh dãy số
n
u
là dãy số tăng.
2) Chứng minh 2022
1 2
2 2 2
1 1 2 2 2022 2022
... 1.
1 1 1
uu u
u u u u u u
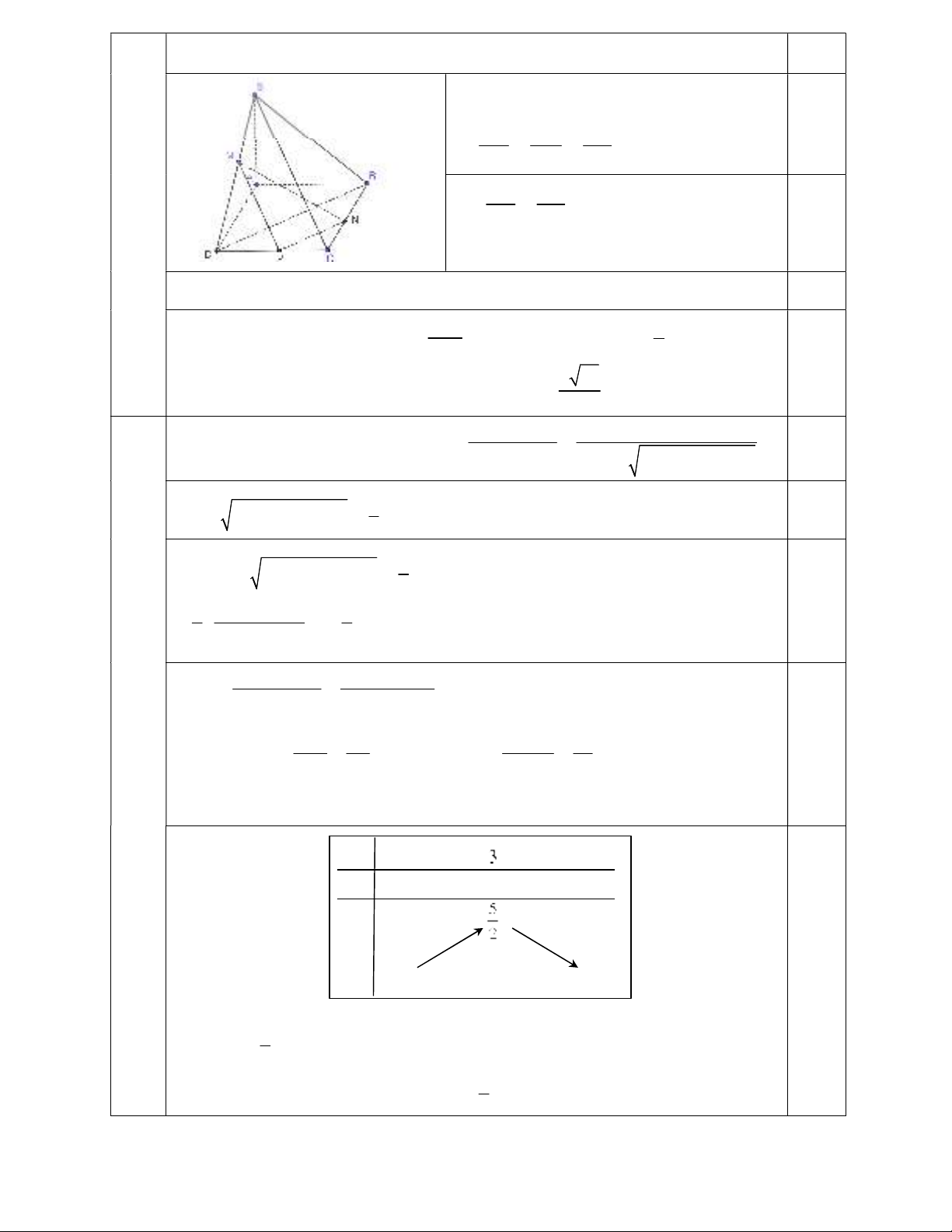
Câu V (4 điểm)
Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
và cạnh bên
SA
vuông
góc với mặt phẳng
( ).
ABCD
Góc giữa đường thẳng
SB
và mặt phẳng
( )
ABCD
bằng
0
60 .
1) Tính khoảng cách giữa hai đường thẳng
SC
và
.
BD
2) Gọi
M
và
N
là hai điểm lần lượt nằm trên hai đoạn thẳng
SD
và
BC
thỏa mãn
.
MS NC
MD NB
Tìm giá trị nhỏ nhất của độ dài đoạn thẳng
.
MN
Câu VI (2 điểm)
Với
, ,
a b c
là các số thực dương, tìm giá trị lớn nhất của biểu thức
16 9
.
1
2 2
Pa b c
a b a c b c
----------------- Hết ----------------
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: .............................................................. Số báo danh: ...........................
Chữ kí của cán bộ coi thi số 1: Chữ kí của cán bộ coi thi số 2:
ĐỀ CHÍNH THỨC
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI THÀNH PHỐ
LỚP 12 THPT NĂM HỌC 2022 - 2023
Môn thi: TOÁN
Ngày thi: 28 tháng 09 năm 2022
HƯỚNG DẪN CHẤM
Câu Nội dung Điểm
I
(4 đ)
1) Viết phương trình tiếp tuyến của
( )
C
biết tiếp tuyến đi qua điểm
(2;3).
M
2,0
Gọi
0 0
( ; )
N x y
là tiếp điểm của tiếp tuyến
cần tìm.
Phương trình
có dạng:
2 3
0 0 0 0
3 3 3 1.
y x x x x x
0,5
Do
(2;3) ,
M
suy ra:
2 3
0 0 0 0
3 3 3 2 3 1
x x x x 0,5
20
3 2
0 0 0 0
0
2
.
3 4 0 2 1 0
1
x
x x x x x 0,5
Từ đó suy ra
: 9 15
y x
hoặc
: 3.
y
0,5
2) Tìm tất cả giá trị của
a
để qua điểm
; 1
A a kẻ được ba tiếp tuyến đến đồ
thị
( )
C
trong đó có hai tiếp tuyến vuông góc với nhau. 2,0
Phương trình tiếp tuyến
tại tiếp điểm
0 0
( ; )
N x y
có dạng:
2 3
0 0 0 0
3 3 3 1.
y x x x x x
Do
( ; 1)
A a
nên ta có:
2 3
0 0 0 0
1 3 3 3 1
x a x x x
0,5
2
0 0 0
1 2 (3 2) 3 2 0
x x a x a
0
2
0 0
1
.
2 (3 2) 3 2 0 (1)
x
x a x a
Từ
A
kẻ được ba tiếp tuyến đến đồ thị
C
khi và chỉ khi PT
(1)
có hai nghiệm phân
biệt khác
1
2
0
3
.
2
2 (3 2) 3 2 0
1
a
a
a a
a
0,5
Do
'(1) 0
f
nên từ
A
kẻ được hai tiếp tuyến vuông góc nhau đến đồ thị
( )
C
khi và
chỉ khi PT
(1)
có hai nghiệm phân biệt
1 2
,
x x
thỏa mãn
1 2
'( ). '( ) 1.
f x f x
0,5
Ta có:
2 2 2 2
1 2 1 2 1 2
'( ). '( ) 1 9 1 1
f x f x x x x x
2
2 2
1 2 1 2 1 2
28
9 2 1 1 9 3 2 1 1 ( ).
27
x x x x x x a a TM
0,5
ĐÁP ÁN CHÍNH TH
Ứ
C
2
II
(5 đ)
1) Giải phương trình 2 2
1 2 2 2 1.
x x x x
2,0
Điều kiện:
2.
x
Ta có:
2
2
2 2 2
1 2 2 2 1 2 1 1 1
x x x x x x 1,0
2 2
1 2 1 0
x x x x
0,5
1 5
2
( ).
1 5
2
x
TM
x
0,5
2) Giải hệ phương trình
3 2
2
3 4 2 1 (1)
.
2 3 9 6 (2)
x x x y y
y x y y 3,0
Điều kiện:
1 9.
y
Ta có:
3
3
(1) 1 1 1 1.
x x y y 0,5
Xét hàm số 3
( ) , .
f t t t t Ta có: 2
'( ) 3 1 0, .
f t t t
Suy ra
( )
f t
đồng biến trên
.
Từ
1 1 1 1.
f x f y x y 0,5
Thay vào
(2)
ta được 2
2 1 3 9 4 0
y y y y
2 1
5 2 0
1 2 9 2
y y
y y
5 ( )
.
2 1
2 0 (*)
1 2 9 2
y TM
y
y y
1,0
Do
2
1
1 2
y
nên
(*) 0
VT
, suy ra PT
(*)
vô nghiệm. 0,5
Với
5 1.
y x
Vậy hệ phương trình có nghiệm
1
.
5
x
y 0,5
III
(2 đ)
Tính xác xuất để số được chọn có các chữ số giống nhau không đứng cạnh nhau.
2,0
Số các số tự nhiên thuộc
A
là:
8!
10080
2!.2!
(số). 0,5
Số các số tự nhiên thuộc
A
có hai chữ số 1 đứng cạnh nhau là:
7!
2520
2!
(số).
Số các số tự nhiên thuộc
A
có hai chữ số 2 đứng cạnh nhau là:
7!
2520
2!
(số).
Số các số tự nhiên thuộc
A
có hai chữ số 1 đứng cạnh nhau và hai chữ số 2 đứng
cạnh nhau là:
6! 720
(số).
0,5
3
Do đó số số tự nhiên thuộc
A
có hai chữ số giống nhau đứng cạnh nhau là:
2520 2520 720 4320
(số). 0,5
Vậy xác suất cần tính là:
4320 4
.
1
10080 7
P 0,5
IV
(3 đ)
1) Chứng minh dãy số
n
u
là dãy số tăng. 2,0
Chứng minh quy nạp
*
0, .
n
u n 0,5
Ta có:
2
*
11 0,
n n n n
u u u u n 0,5
*
1 1
2, .
n n n
u u u u n 0,5
Suy ra
2*
11 0,
n n n n
u u u u n
n
u
là dãy số tăng. 0,5
2) Chứng minh 1 2 2022
2 2 2
1 1 2 2 2022 2022
... 1.
1 1 1
u u u
u u u u u u
1,0
Ta có:
2
1
1 1 1
n n n n
u u u u
2
12
1
1 1
1 1 1 1 1
1
n
n n n n
n n
n n
u
u u u u u u u u
2
1
1 1
.
1 1
1
n
n n
n n
u
u u
u u
0,5
2022
2
1
1 2023
1 1
1.
1 1
1
n
n
n n
u
u u
u u 0,5
V
(4 đ)
1) Tính khoảng cách giữa hai đường thẳng
SC
và
.
BD
2,0
Ta có
0
60 .tan 3.
SBA SA AB SBA a
Chứng minh được
( ).
BD SAC
0,5
Gọi
O
là tâm của hình vuông
.
ABCD
Kẻ
OK SC
tại
.
K
Chứng minh được
OK
là đoạn vuông góc chung của hai đường
thẳng
SC
và
.
BD
0,5
Chứng minh được
.
CKO CAS
0,5
Ta có
2
BD a
và
5
SC a
. 30
.
10
SAOC a
OK
SC
0,5
4
2) Tìm giá trị nhỏ nhất của độ dài đoạn thẳng
.
MN
2,0
Kẻ
MP SC P CD
.
NC MS PC
NP BD
NB MD PD
0,5
Đặt
(0 1).
SM CN
x x
SD CB
Ta có
(1 ) .

MN MP PN x SC xDB
0,5
Chứng minh được
2 2 2 2 2
(1 ) .
MN x SC x DB
0,5
Suy ra
2
2 2 2
10
.
(7 10 5)
7
a
MN x x a Dấu bằng xảy ra khi
5
( ).
7
x TM
Vậy giá trị nhỏ nhất của độ dài đoạn thẳng
MN
bằng
70
.
7
a
0,5
VI
(2 đ) Tìm giá trị lớn nhất của biểu thức
16 9
.
1
2 2
Pa b c
a b a c b c
2,0
Ta có
1
2 2 4
2
a c b c a b c
0,5
2
2
1
2 2 3 3 4
6
1 4 4 4 2 .
6 2 3
a b a c b c a b a b c
a b c a b c
0,5
2
16 27
.
12
Pa b c
a b c
Xét hàm
2
16 27
, 0
1
2
f t t
t
t
có
2 3
16 27
.
'
( 1)
f t
t t
Ta có
'( ) 0 3.
f t t
0,5
Bảng biến thiên
Suy ra
5
.
2
P Dấu bằng xảy ra khi
1.

a b c
Vậy giá trị lớn nhất của biểu thức
P
bằng
5
.
2
0,5
t
0
+
∞
f
'
(t)
+
0
–
f(t)
–
∞
0