SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT PHAN HUY CHÚ–QUỐC OAI
KÌ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
Môn : Toán – Khối: 10
Năm học : 2024-2025
Thời gian làm bài: 120 phút
Câu 1.(4,0 điểm)
a. Cho hai tập hợp và . Tìm .
b. Cho hai tập hợp với là tập hợp khác rỗng. Có bao nhiêu giá trị nguyên của thuộc
để
Câu 2.(4,0 điểm)
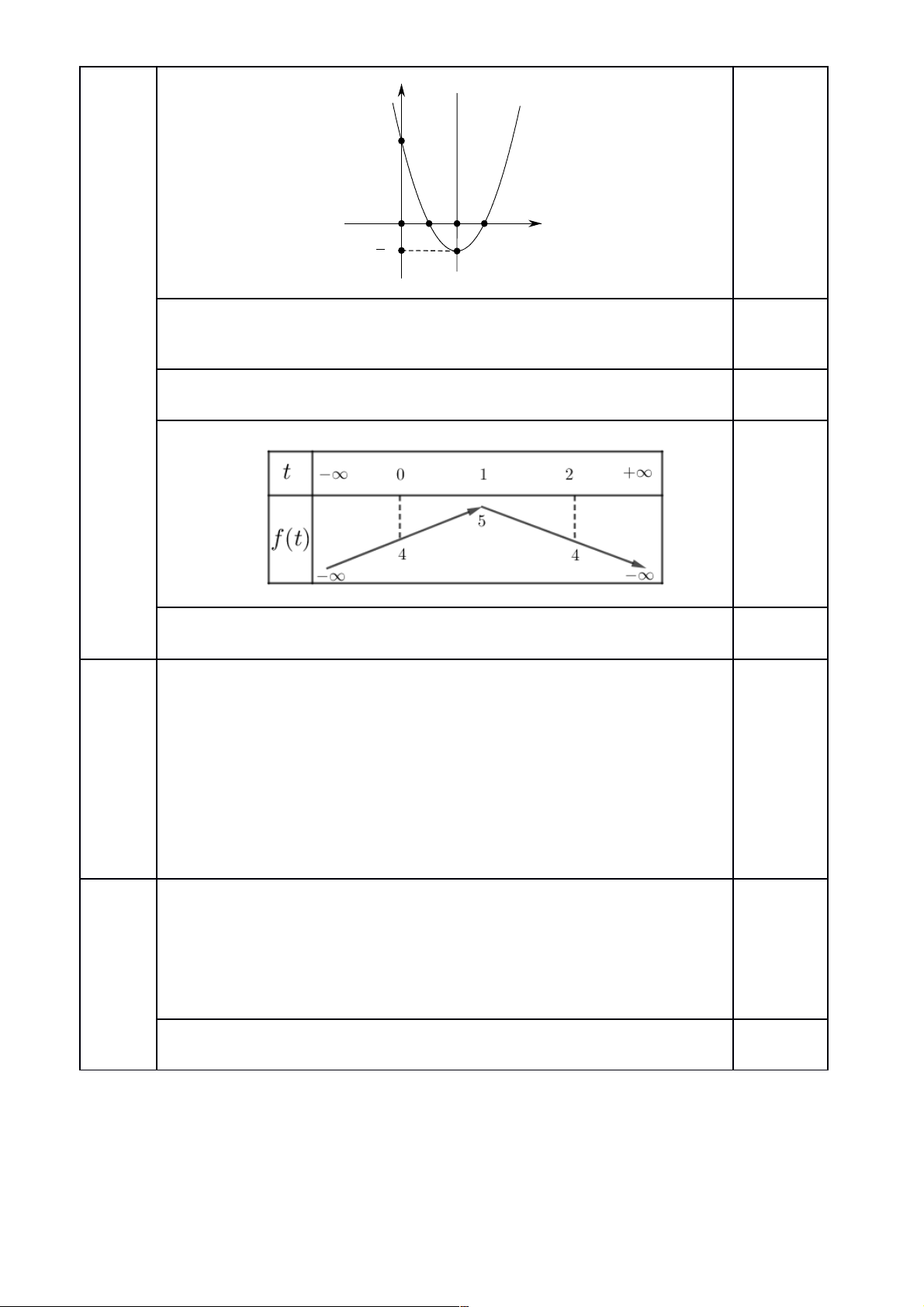
a. Vẽ đồ thị hàm số .
b. Tìm tất cả các tham số để phương trình sau có nghiệm thực
Câu 3.(3,0 điểm)
Một xưởng sản xuất hai loại sản phẩm loại I và loại II từ 200kg nguyên liệu và một
máy chuyên dụng. Để sản xuất được một kilôgam sản phẩm loại I cần 2kg nguyên
liệu và máy làm việc trong 3 giờ. Để sản xuất được một kilôgam sản phẩm loại II cần
4kg nguyên liệu và máy làm việc trong 1,5 giờ. Biết một kilôgam sản phẩm loại I lãi
300000 đồng, một kilôgam sản phẩm loại II lãi 400000 đồng và máy chuyên dụng
làm việc không quá 120 giờ. Hỏi xưởng cần sản xuất bao nhiêu kilôgam sản phẩm
mỗi loại để tiền lãi lớn nhất.
Câu 4. (3,0 điểm)
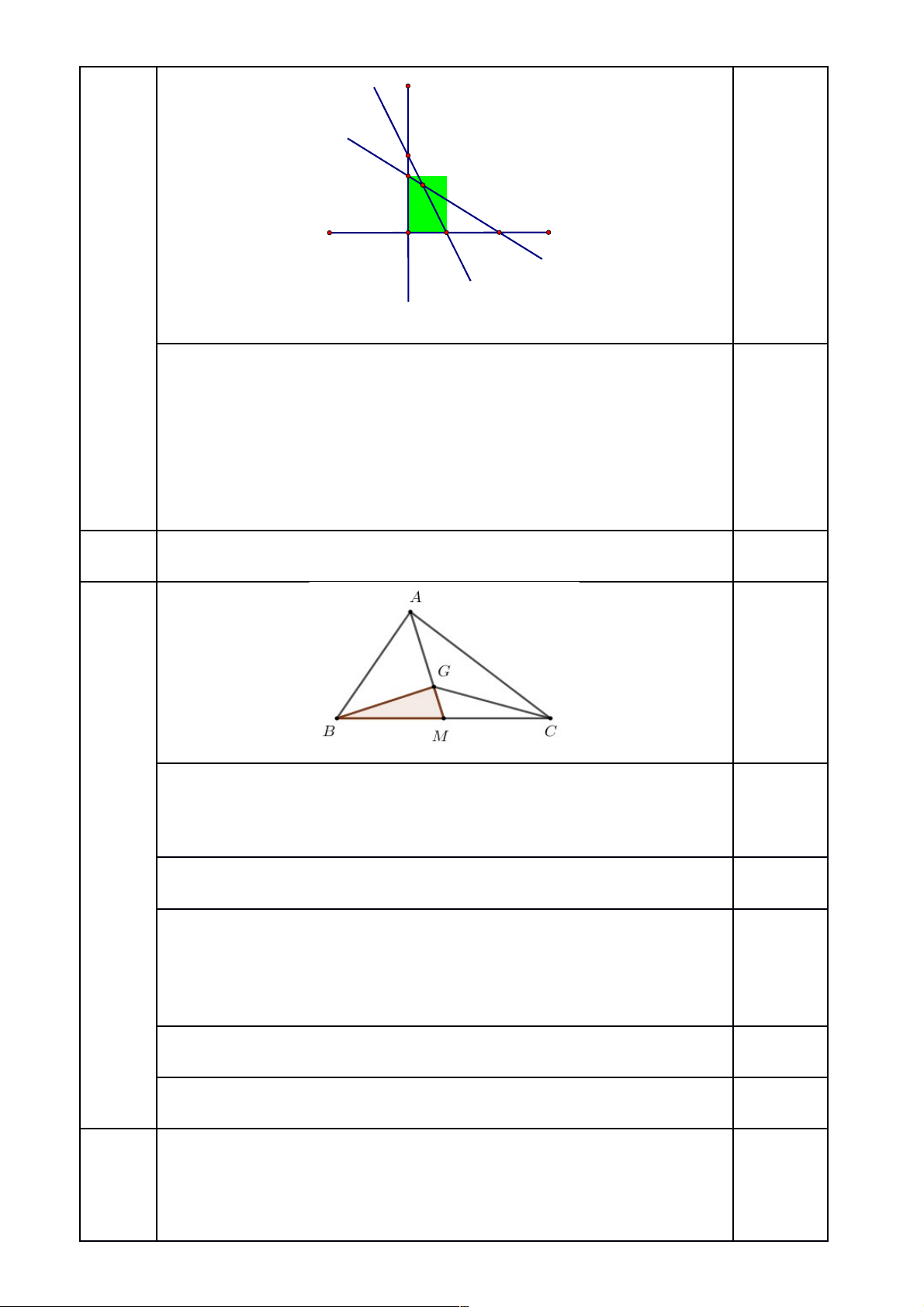
Cho tam giác thỏa mãn: và . Gọi là trung điểm của cạnh và là trọng tâm của tam
giác . Tìm diện tích tam giác .
Câu 5.(4,0 điểm)
a. Cho hình bình hành . Trên đường chéo lấy các điểm và sao cho . Gọi là giao
điểm của và ; là giao điểm của và . Chứng minh:
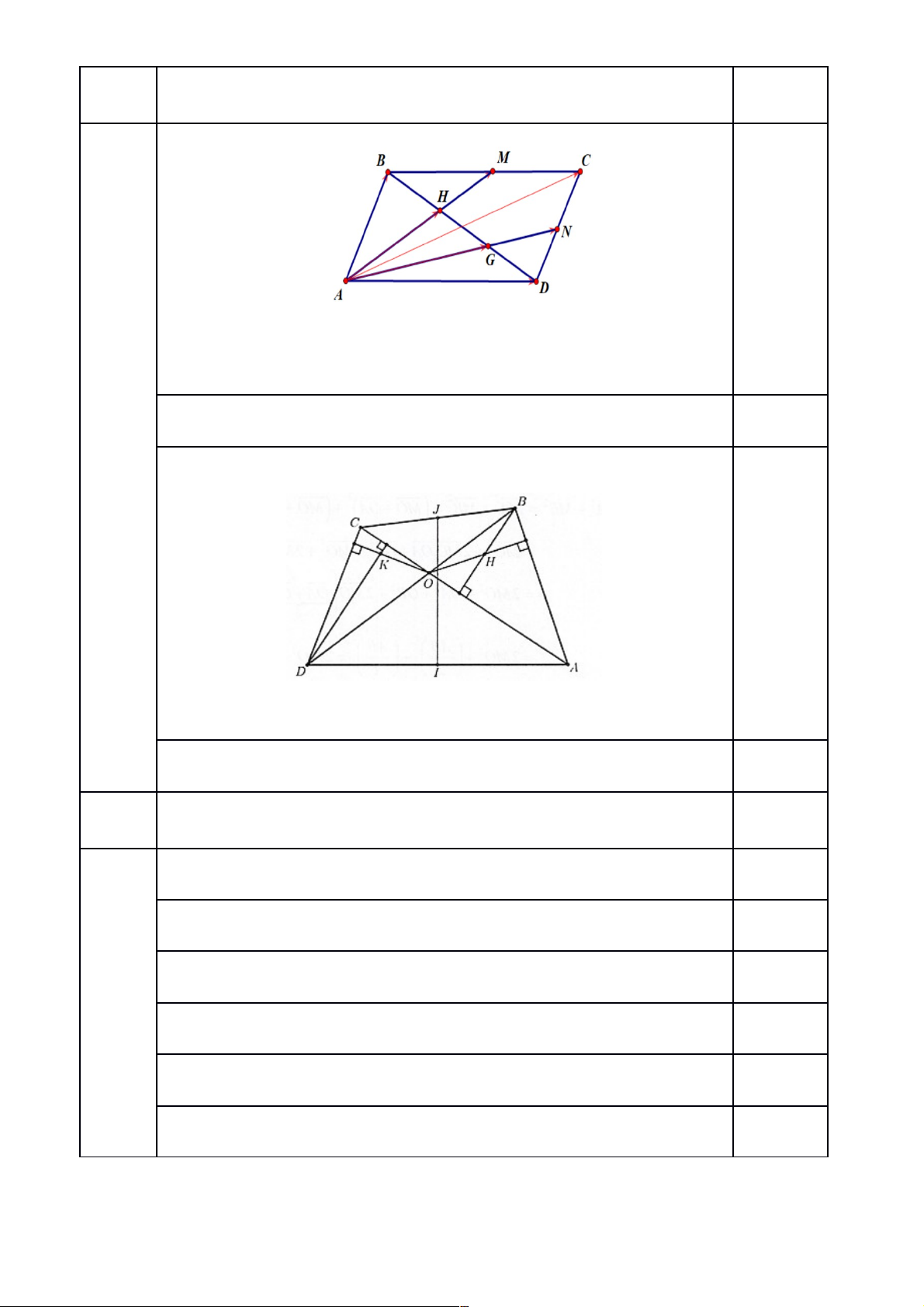
b. Cho tứ giác lồi , hai đường chéo và cắt nhau tại điểm . Gọi điểm , lần lượt là trực
tâm các tam giác và . Gọi điểm lần lượt là trung điểm của cạnh và . Chứng minh
rằng .
Câu 6. (2,0 điểm)
Cho các số thực thỏa mãn và Tìm giá trị lớn nhất và nhỏ nhất của biểu thức