PHÒNG GIÁO DỤC – ĐÀO TẠO
TIỀN HẢI
ĐỀ KHẢO SÁT HỌC SINH GIỎI CẤP HUYỆN
Năm học 2023 - 2024
Môn: TOÁN 6
(Thời gian làm bài 120 phút)
Bài 1. (4,5 điểm)
1) Thực hiện phép tính:
202.25 303.9 101.67+−
2) Tìm số tự nhiên x, biết:
( )
1 3 5 7 9 ... 2x –1 400+ + + + + + =
3) Tính giá trị biểu thức:
2 3 2023
2025
A1 2 2 2 ... 2
22
=+ + + + +
−
Bài 2. (4,5 điểm)
1) Tìm số nguyên tố p sao cho các số p + 2; p + 8 và p + 28 là các số nguyên tố.
2) Cho a, b là các số nguyên, chứng tỏ rằng nếu:
(2a 3b) 7+
thì
(8a 5b) 7+
3) Chứng minh phân số
2
2
2n 3
3n 5
+
+
là phân số tối giản với mọi số nguyên n.
Bài 3. (3,0 điểm)
1) Tìm hai số nguyên x và y, biết:
6xy 2x 3y 2− + =
2) Số học sinh tham quan của một trường THCS khoảng từ 500 đến 800 em. Nếu
thuê các xe 30 chỗ thì thừa 22 ghế, nếu thuê các xe 35 chỗ thì thừa 27 ghế, nếu thuê các xe
45 chỗ thì thiếu 8 ghế. Hỏi có tất cả bao nhiêu học sinh đi tham quan (biết rằng mỗi học sinh
ngồi một ghế).
Bài 4. (6,0 điểm)
1) Trên tia Ox lấy điểm A sao cho
OA 6cm=
. Vẽ Oy là tia đối của tia Ox, trên tia
Oy lấy điểm B sao cho
1
OB .OA
3
=
a) Tính độ dài đoạn thẳng OB.
b) Vẽ điểm C là trung điểm của đoạn thẳng AB. Chứng tỏ
AB 4.OC=
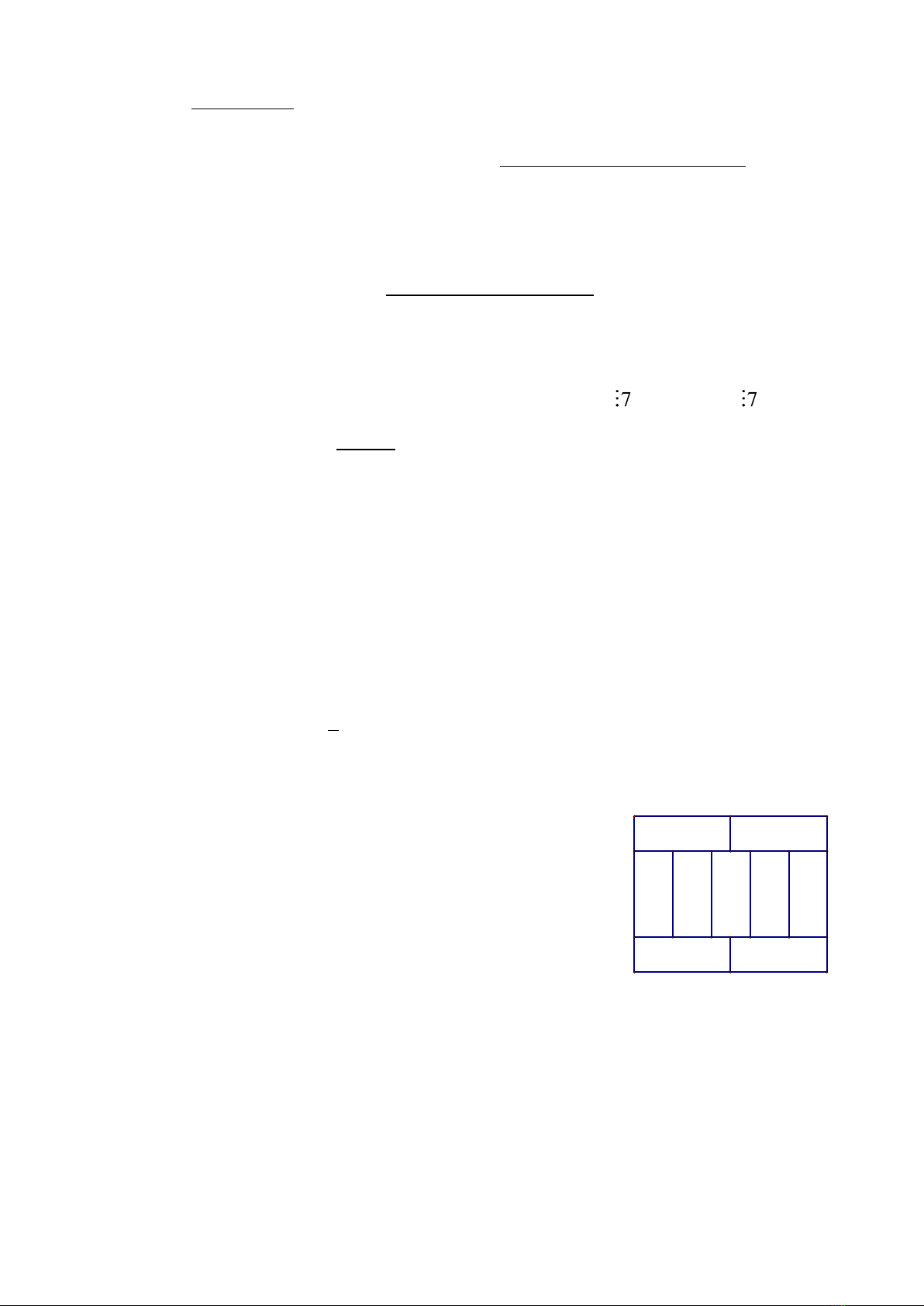
2) Một mảnh vườn hình chữ nhật có chu vi là 76 m được
chia thành 9 hình chữ nhật nhỏ có các chiều dài bằng nhau và
các chiều rộng bằng nhau (như hình vẽ bên). Tính chiều dài và
chiều rộng của mảnh vườn ban đầu.
3) Cho
121
điểm phân biệt trong đó chỉ có
21
điểm thẳng hàng, ngoài ra không có 3
điểm nào khác thẳng hàng. Qua 2 điểm phân biệt ta kẻ 1 đường thẳng. Hỏi kẻ được tất cả
bao nhiêu đường thẳng phân biệt từ
121
điểm nói trên.
Bài 5. (2,0 điểm)
Tìm ba số nguyên tố đôi một khác nhau a, b, c biết:
2 2 2
a b c 5070+ + =
_____Hết_____
Họ và tên thí sinh: .......................................................... Số báo danh:..........
Thí sinh không được sử dụng máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Chữ kí cán bộ coi thi 1………………..……… Chữ kí cán bộ coi thi 2……..…………………