TR NG THPT TH CH THÀNH IƯỜ Ạ
T TOÁN - TINỔ
Đ THI MÔN TOÁN_KH I 10 (l n 1)Ề Ố ầ
Năm h c: 2022 - 2023ọ
Th i gian: ờ120 phút (không k th i gian giao để ờ ề)
Câu 1: (1 đi m)ể
1. Cho hai t p h p ậ ợ
{ }
1,2,3,4A
=
;
{ }
1,3,6B=
. Tìm
; \A B A B
.
2. L p m nh đ ph đnh c a m nh đ sau và xét tính đúng sai c a nó: M i hình vuông đu làậ ệ ề ủ ị ủ ệ ề ủ ọ ề
hình thoi.
Câu 2: (1 đi m)ể Gi i các ph ng trình:ả ươ
a)
3 5 9 3 2x x x− + − = − +
. b)
( ) ( ) ( ) ( )
2 4038 2 2 4038 2x x x x− − = − +
.
Câu 3: (2 đi m)ể
1. Tìm t p xác đnh c a hàm s : ậ ị ủ ố
1 4 1 2y x x= − − +
.
2. Tìm
,a b
đ đng th ng ể ườ ẳ
y ax b= +
c t tr c hoành t i đi m có hoành đ b ng ắ ụ ạ ể ộ ằ
, c t tr cắ ụ
tung t i đi m có tung đ b ng 6.ạ ể ộ ằ
3. Bi t đi m ế ể
thu c đ th hàm s ộ ồ ị ố
3 2 1 2y x x x= − − + + + −
và
có hoành đ b ng ộ ằ
1−
.
Hãy tìm tung đ đi m ộ ể
.
4. Xác đnh hàm s b c hai ị ố ậ
2
1
2
y x bx c= − + +
, bi t r ng đ th c a nó có hoành đ đnh là 2 vàế ằ ồ ị ủ ộ ỉ
đi qua đi m ể
( )
4; 18M− −
.
Câu 4: (2 đi m)ể
1. L p b ng bi n thiên và v đ th c a hàm s ậ ả ế ẽ ồ ị ủ ố
2
4 5y x x= − + +
.
2. Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố
m
đ đng th ng ể ườ ẳ
y m=
c t đ th hàm sắ ồ ị ố
2
4 5y x x= − + +
t i hai đi m ạ ể
,A B
sao cho vect ơ
AB
uuur
có hoành đ b ng ộ ằ
4 2
.
Câu 5: (2 đi m)ể
Cho hình bình hành
ABCD
có tâm
O
,
N
là trung đi m c a c nh ể ủ ạ
AB
,
G
là tr ng tâm tam giácọ
ABC
.
1. Ch ng minh ứ
AB AC OA OD− = −
uuur uuur uuur uuur
.
2. Tìm đi m ể
th a mãnỏ
4MA MB MC MD+ + =
uuur uuur uuuur uuuur
.
3. Phân tích vect ơ
GA
uuur
theo hai vect ơ
BD
uuur
và
NC
uuur
.
4. Bi t tam giác ế
ABC
là tam giác cân,
ﾷ
, 120AB a ABC= =
o
. Tính đ dài c a vect ộ ủ ơ
BA BC+
uuur uuur
theo
a
.
Câu 6: (1 đi m) ểTrong m t ph ng t a đ ặ ẳ ọ ộ
Oxy
, cho
2 3v i j= − +
r r r
,
( )
3; 5A−
.
1. Tìm t a đ c a vect ọ ộ ủ ơ
v
r
.
2. Tìm t a đ đi m ọ ộ ể
B
sao cho
AB v=
uuur r
.
3. Tìm t a đ đi m ọ ộ ể
thu c tr c hoành sao cho ba đi m ộ ụ ể
, ,A B M
th ng hàng.ẳ
Câu 7: (1 đi m)ể
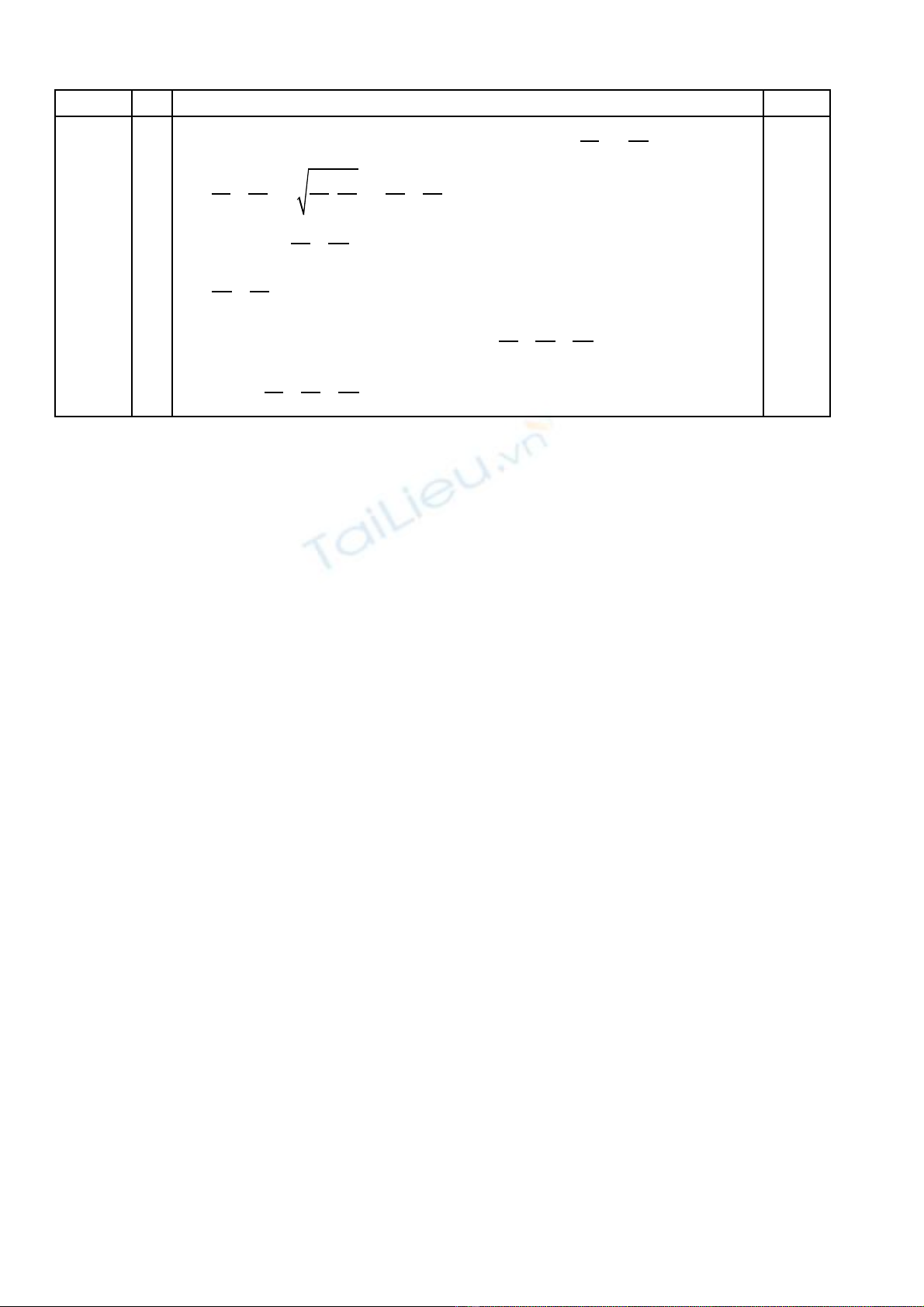
Cho các s th c ố ự a, b, c > 0. Ch ng minh r ng: ứ ằ
.
bc ca ab abc
a b c
+ + + +
------------- H T Ế-------------
ĐÁP ÁN
CâuÝ Đáp ánĐi mể
1 1
{ } { }
1;2;3;4;6 , \ 2;4A B A B= =�
.0,5
2Có ít nh t m t hình vuông không ph i là hình thoi. M nh đ sai.ấ ộ ả ệ ề 0,5
2 a Ph ng trình vô nghi m.ươ ệ 0,5
b
2019x
=
.0,5
3 1
1 1
;
2 4
� �
−
� �
� �
.0,5
2
3, 6a b= =
.0,5
3
6
M
y=
.0,5
4
2
12 2
2
y x x= − + −
.0,5
4 1 - V b ng bi n thiên.ẽ ả ế 0,5
- V đ th .ẽ ồ ị 0,5
2Ph ng trình hoành đ giao đi m: ươ ộ ể
2 2
4 5 4 5 0x x m x x m− + + = − − + =�
.
Ph ng trình có nghi m ươ ệ
9m
. G i ọ
1 2
,x x
là các nghi m c a ph ngệ ủ ươ
trình. Khi đó
( ) ( ) ( )
1 2 2 1
; , ; , ;0A x m B x m AB x x= −
uuur
.
0,5
Theo bài ra, ta có
2 1
4 2x x− =
. Mà
1 2 1 2
4, . 5x x x x m+ = = −
(Đnh lí Viet)ị
nên suy ra
1m
=
(th a mãn đi u ki n). V y ỏ ề ệ ậ
1m
=
.
0,5
5 1
AB AC CB DA OA OD− = = = −
uuur uuur uuur uuur uuur uuur
.0,5
2
4 4MA MB MC MD MD DA MD DB MD DC MD+ + = + + + + + =�
uuur uuur uuuur uuuur uuuur uuur uuuur uuur uuuur uuur uuuur
2 2DA DC DB MD DB MD DM BD+ + = = =� � �
uuur uuur uuur uuuur uuur uuuur uuuur uuur
. V y ậ
là đi m ể
xác đnh b i ị ở
2DM BD=
uuuur uuur
.
(Cách khác:
4 3 4MA MB MC MD MG MD+ + = =�
uuur uuur uuuur uuuur uuuur uuuur
).
0,5
3
( )
1; 2 ;
3
GA AG AB AC BD AD AB BC AB AC AB= − = − + = − = − = −
uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur
( )
1 1 ;
2 2
NC CN CA CB AB AC= − = − + = − +
uuur uuur uuur uuur uuur uuur
0,25
1 1 1
2
3 2 3
1 2
3 3
x y x
GA xBD yNC
x y y
� �
− = − − =
� �
� �
= + ��
� �
� �
− = + = −
� �
� �
uuur uuur uuur
.
V y ậ
1 2
3 3
GA BD NC= −
uuur uuur uuur
.
0,25
4T gi thi t suy ra tam giác ừ ả ế
ABD
đu c nh ề ạ
a
.
V y ậ
BA BC BD a+ = =
uuur uuur uuur
.
0,5
6 1
( )
2;3v= −
r
.0,25
2
( )
1; 2B−
.0,25
3G i ọ
( )
;0M x
. Ta có M, A, B th ng hàng ẳ
,MA ABuuur uuur
cùng ph ng.ươ
( )
3 ; 5MA x= − −
uuur
.
3 5 1
2 3 3
xx
−= − = −�
−
. V y ậ
1;0
3
M� �
−
� �
� �
0,5
CâuÝ Đáp ánĐi mể
7Áp d ng b t đng th c Cô-si cho hai s d ng ụ ấ ẳ ứ ố ươ
bc
a
và
ca
b
, ta có:
2 . 2
bc ca bc ca bc ca c
a b a b a b
+ +�� �
(1).
T ng t ươ ự
2
ca ab a
b c
+
(2).
2
ab bc b
c a
+
(3).
C ng (1), (2), (3) theo v ta đc: ộ ế ượ
2 2( )
bc ca ab a b c
a b c
� �
+ + + +
� �
� �
.
Suy ra
.
bc ca ab abc
a b c
+ + + +
1,0