KY THI OLYMPIC TRUYÊN THÔNG 30/4
LÂN TH XIII TAI THANH PHÔ HUÊ Ư
ĐÊ THI MÔN TOÁN L P 11Ớ
Th i gian lam bai: 180 phútơ
Chu y: Môi câu hoi thi sinh lam trên 01 t giây riêng biêt ơ
Câu 1 (4 đi mể).
Gi i h ph ng trình sau:ả ệ ươ
+++=++ +
+
=
−
1)2yx(log2)6y2x(log3
1y
1x
e
23
2
2
xy 22
Câu 2 (4 đi mể).
Cho hình chóp đ u S.ABCD có c nh đáy b ng d và s đo c a nh di n [B,SC,D]ề ạ ằ ố ủ ị ệ
b ng 150ằ0. Tính th tích c a hình chóp đ u S.ABCD theo d.ể ủ ề
Câu 3 (4 đi m).ể
Cho dãy s d ng (aố ươ n).
a. Ch ng minh r ng v i m i s nguyên d ng k :ứ ằ ớ ọ ố ươ
( )
+
++++
+
≤−k
1k
k
3
2
3
2
2
1
kk21 a
k
1k
...a
3
4
a
2
3
a2
)1k(k
1
a...a.a
b. Bi t ế
∈=
∑
=
∞→ aalim
n
1i
i
n
R. Đ t bặn =
nn21
3321211 a...aa...aaaaaa ++++
v i nớ
1
≥
Ch ng minh r ng dãy (bứ ằ n) có gi i h n.ớ ạ
Câu 4 (4 đi m).ể
Cho hàm s f(x) = 2x – sinx.ố
Ch ng minh r ng t n t i h ng s b và các hàm s g, h tho mãn đ ng th i các ứ ằ ồ ạ ằ ố ố ả ồ ờ
đi u ki n sau: ề ệ
1) g(x) = bx + h(x) v i m i s th c x. ớ ọ ố ự
2) h(x) là hàm s tu n hoàn. ố ầ
3) f(g(x)) = x v i m i s th c x.ớ ọ ố ự
Câu 5 (4 đi m).ể
Tìm t t c các s t nhiên m, n sao cho đ ng th c sau đúng:ấ ả ố ự ẳ ứ
8m = 2m + n(2n-1)(2n-2)
-------------------H T-------------------Ế
Ghi chú: Cán b coi thi không gi i thích gì thêmộ ả
ĐÁP ÁN TOÁN L P 11Ớ
N I DUNGỘĐI MỂ
C âu 1: Gi i h ph ng trình ả ệ ươ
2 2 2
2
3 2
1(1)
1
3log ( 2 6) 2log ( 2) 1 (2)
y x x
ey
x y x y
−
+
=
+
+ + = + + +
Đk: x + 2y +6 > 0 và x + y + 2 > 0 0,5
Ph ng trình (1) ươ ⇔ y2 – x2 = ln(x2+1) – ln(y2+1)
⇔ ln(x2+1)+ x2 +1 = ln(y2+1)+y2+1 (3)
Xét hàm s f(t) = lnt + t v i t ố ớ ≥ 1
Ph ng trình (3) có d ng f(xươ ạ 2+1) = f(y2+1) (4)
Ta có f(t) đ ng bi n trên [1ồ ế ;+
∞
).
Do đó (4) ⇔ x2+1 = y2+1 ⇔ x = ± y
1
* V i x = -y , t (2) ta đ c ớ ừ ượ
3
log (6 ) 1x− =
, v i x<6ớ
⇔ x = 3 ⇒ y = -3 (th a mãn h )ỏ ệ 0.5
* V i x = y , t (2) ta đ cớ ừ ượ
v i x > -1ớ0.5
Đ t ặ
= 6u ⇒
2
3
2 3
1 2
u
u
x
x
+ =
+ =
⇒ 1+23u = 32u ⇔
1 8 1
9 9
u u
+ =
÷ ÷
(5)
Xét g(u) =
1 8
9 9
u u
+
÷ ÷
, g(u) là hàm ngh ch bi n trên R và có g(1) = 1 nênị ế
u = 1 là nghi m duy nh t c a (5).ệ ấ ủ
V i u = 1 suy ra x = y = 7 (th a mãn h )ớ ỏ ệ
1
V y h có 2 nghi m (3ậ ệ ệ ;-3) , (7 ;7) 0.5
N I DUNGỘĐI MỂ
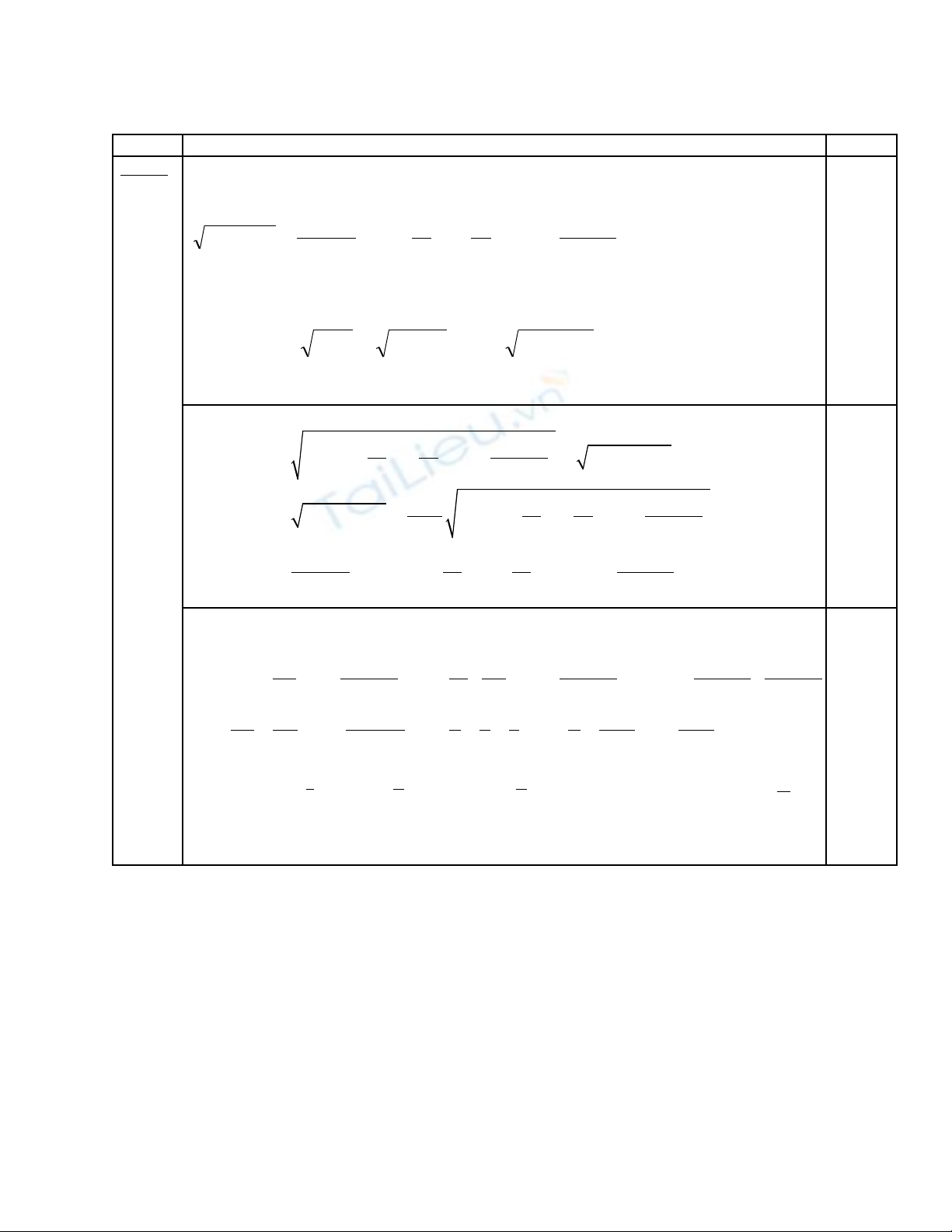
C âu 2: Cho hình chóp đ u S.ABCD có c nh đáy b ng d và s đo c a nh di nề ạ ằ ố ủ ị ệ
[B,SC,D] b ng 150ằ0. Tính th tích c a hình chóp để ủ ều S.ABCD theo d.
Ta có: BD
⊥
SC . Dựng mặt phẳng qua BD vuoâng goùc vôùi SC
taïi P.
Ta coù :
0
150BPD =∠
1
Ta có: cos1500 =
2
2
2
22
BP2
BD
1
BP2
BDBP2 −=
−
(1) 0.5
G i M là trung đi m c a BC. Ta có SM .BC = BP.SC.ọ ể ủ
BC = d, g i h là chi u cao hình chóp S.ABCDọ ề
Ta có: SM2 = h2 +
4
d
2
; SC2 = h2 +
2
d
2
. Suy ra: BP2 =
)dh2(2
)dh4(d
22
222
+
+
1
(1) tr thành:ở
22
2
dh4
d
2
3
+
−=−
. Suy ra: h =
3
332
2
d−
1
VS.ABCD =
6
d
dtABCD.h
3
13
=
3
332 −
0.5
N I DUNGỘĐI MỂ
C âu 3 Cho dãy s d ng (aố ươ n).
a. Ch ng minh r ng v i m i s nguyên d ng k: ứ ằ ớ ọ ố ươ
( )
+
++++
+
≤−k
1k
k
3
2
3
2
2
1
kk21 a
k
1k
...a
3
4
a
2
3
a2
)1k(k
1
a...a.a
b. Bi t ế
∈=
∑
=
∞→ aalim
n
1i
i
n
R.
Đ t bặn =
nn21
3321211 a...aa...aaaaaa ++++
v i nớ
1
≥
Ch ng minh r ng dãy (bứ ằ n) có gi i h n.ớ ạ
a)Ta có
2 3
1 2 3 1 2 3
2 1
2 3
1 2 3 1 2 3 2 1
2 3
1 2 3 2 1
3 4 ( 1)
( 2)( )( )....( ) .... ( 1)
23
1 3 4 ( 1)
.... ( 2)( )( )....( )
1 2 3
1 3 4 ( 1)
( 2) ( ) ( ) .... ( )
( 1) 2 3
k
k
kk k
k
k
kk
k k k
k
kk
k
a a a a a a a a k
k
k
a a a a a a a a
kk
k
a a a a
k k k
−
−
−
+= + ⇒
+
= ≤
+
+
+ + + +
+
2
b)
T câu a) suy raừ
2
1 2 1
1 1 3 1 1 ( 1) 1
( 2)( .. ) ( )( .... ) .. ( )( )
1.2 ( 1) 2 2.3 ( 1) ( 1)
n
n n n
n
b a a a
n n n n n n
n
−
+
≤ + + + + + + +
+ + +
Do :
1
1n
1
1
1n
1
n
1
...
3
1
2
1
2
1
1
)1n(n
1
...
3.2
1
2.1
1<
+
−=
+
−++−+−=
+
+++
nên
1 2
1 2
1
1 1 1
(1 ) (1 ) ... (1 ) ( )
1 2
n
n
n n i
i
b a a a e a
n
=
≤ + + + + + + < ∑
v i ớ
n
nn
1
1lime
+= ∞→
(bn) tăng và b ch n trên, do đó có gi i h n. ị ặ ớ ạ
2
N I DUNGỘĐI MỂ
C âu 4: Cho hàm s f(x)= 2x – sinx.ố
Ch ng minh r ng t n t i h ng s b và các hàm s g, h th a mãn đ ng th iứ ằ ồ ạ ằ ố ố ỏ ồ ờ
các đi u ki n sau :ề ệ
1) g(x) = bx + h(x) v i m i s th c x.ớ ọ ố ự
2) h(x) là hàm s tu n hòan.ố ầ
3) f(g(x)) = x v i m i s th c x.ớ ọ ố ự
T đi u ki n 3) cho th y mu n ch ng t t n t i g ch c n ch ng t f cóừ ề ệ ấ ố ứ ỏ ồ ạ ỉ ầ ứ ỏ
hàm s ng c.ố ượ
Chú ý : f đ ng bi n trên (-ồ ế
∞
;+
∞
) nên có hàm s ng c g.ố ượ
Ta có : f(g(x)) = x và g(f(x)) = x v i m i s th c x.ớ ọ ố ự
1
Đ t : h(x) = g(x) – bx. Ta s ch n b đ h(x) tu n hòan.ặ ẽ ọ ể ầ 0.5
Hàm sinx tu n hoàn chu kì 2ầ
π
.
Ta s ch ng t g(x+ 4ẽ ứ ỏ
π
) = g(x) +2
π
v i m i s th c x.ớ ọ ố ự
Th t v y : g(x)+2ậ ậ
π
= [f(g(x) +2
π
)] = g[2(g(x)+2
π
) - sin(g(x)+2
π
)]
=g[2g(x)-sin(g(x)) + 4
π
] = g[f(g(x)) + 4
π
] = g( x +4
π
).
1
T đó : h(x+4ừ
π
) = g(x + 4
π
) – b(x+4
π
) = g(x) + 2
π
-bx – 4b
π
= h(x) + 2
π
(1-2b). 1
N u ch n b =ế ọ
2
1
thì h(x + 4
π
) = h(x) v i m i s th c x.ớ ọ ố ự 0.5