Ngày 25 tháng 10 năm 2018
Tiêt 16: KI M TRA CH NG IỂ ƯƠ
A. M C ĐÍCHỤ
Ki n th c:ế ứ Ki m tra vi c ti p thu các ki n th c c b n c a ch ng: Quan h gi aể ệ ế ế ứ ơ ả ủ ươ ệ ữ
đng cao và c nh trong tam giác vuông; t s LG, Quan h gi a c nh và góc trongườ ạ ỉ ố ệ ữ ạ
tam giác vuông.
K năngỷ: Ki m tra kh năng v n d ng các ki n th c c a ch ng đ gi i các bài t p.ể ả ậ ụ ế ứ ủ ươ ể ả ậ
Thái độ: C n th n, chính xác trong làm bài ki m tra.ẩ ậ ể
Năng l cự: Tính toán, l p lu n chính xác, ch t ch , linh ho t.ậ ậ ặ ẽ ạ
B. HÌNH TH CỨ: T lu n.ự ậ
C. MA TR N ĐẬ Ề:
N i dungộNh n bi tậ ế Thông hi uểV n d ng 1ậ ụ V n d ngậ ụ
2T ngổ
1. M t s h th cộ ố ệ ứ
v c nh và đngề ạ ườ
cao trong tam giác
vuông
(4ti t)ế
Bi t dùng cácế
công th c vứ ề
c nh và đngạ ườ
cao đ tính tr cể ự
ti p các đo nế ạ
th ng trong tamẳ
giác vuông.
Phát hi n ra ệ
tam giác
vuông đ ể
v n d ng h ậ ụ ệ
th c vào c/m ứ
tính toán.
S câuố
S đi mố ể
%
1 câu
2đ
20
1 câu
1đ
10
2 câu
3đ
30
2. T s l ng giác ỉ ố ượ
c a góc nh n.ủ ọ
(4 ti t)ế
Dùng đ/n, t/c
t s l ng ỉ ố ượ
giác đ so ể
sánh tính giá
tr các t s ị ỉ ố
l ng giác.ượ
S câuố
S đi mố ể
%
1 câu
3đ
30
2 câu
3đ
30
3. + M t s h th cộ ố ệ ứ
v c nh và gócề ạ
trong tam giác
vuông.
+ ng d ng th c t Ứ ụ ự ế
c a t s l ng giác.ủ ỉ ố ượ
(7 ti t)ế
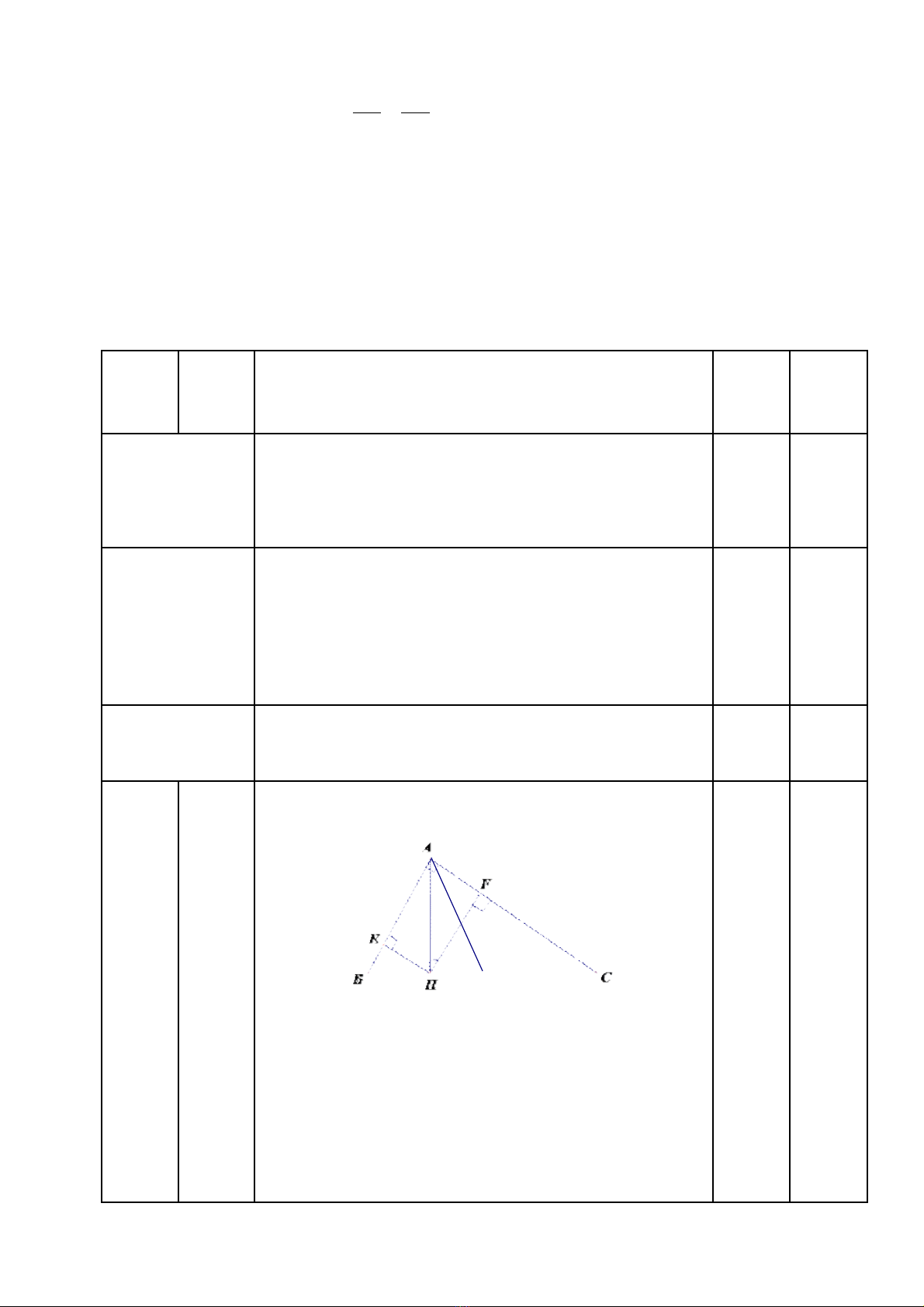
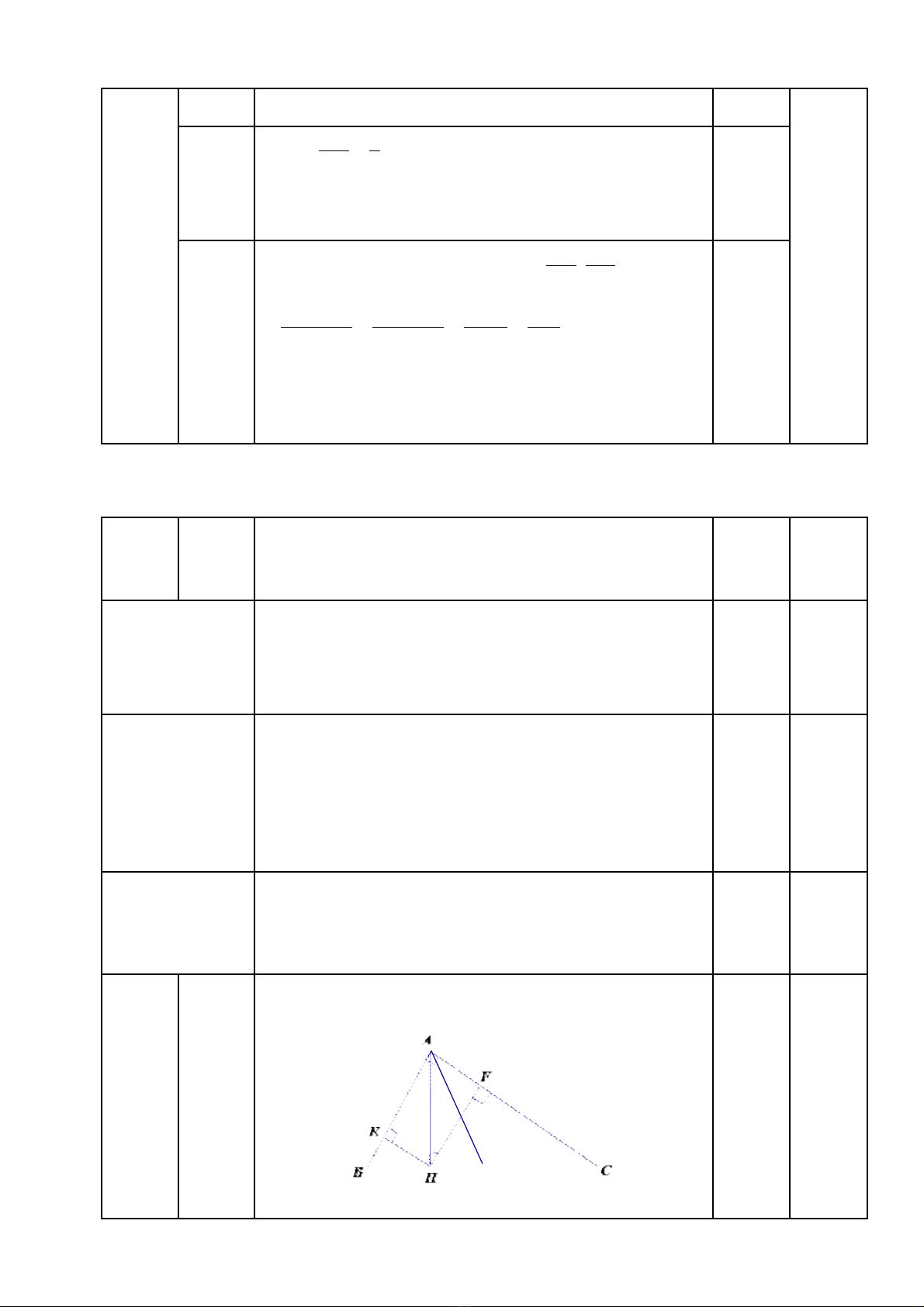
Gi i bài toán ả
th c t ; tính ự ế
toán nh gi iờ ả
tam giác
vuông.
V n d ng ậ ụ
ki n th c ế ứ
t ng h p ổ ợ
đ tính ể
toán ,
ch ng ứ
minh.
S câuố
S đi mố ể
%
2 câu
3đ
30
1câu
1đ
10
3 câu
4đ
40
S câuố
S đi mố ể
%
1 câu
2đ
20
2 câu
3đ
30
3 câu
4đ
40
1 câu
1đ
10
7 câu
10đ
100
IV. Đ BÀIỀ
Đ 1ề
Bài 1 : (2 đi m)ể
Cho tam giác ABC vuông t i A, k đng cao AH, bi t BH = 4, CH = 9. Tính đạ ẻ ườ ế ộ
dài AH.
Bài 2 : (3 đi m)ể
S p x p các t s l ng giác sau theo th t tăng d n:ắ ế ỉ ố ượ ứ ự ầ
sin240 , cos350 , sin540 , cos700 , sin780 , cos450.
Bài 3 : (1,5 đi m)ể
M t c t c có bóng n ng trên m t đt dài 4m. Bi t góc mà tia sáng m t tr i t oộ ộ ờ ắ ặ ấ ế ặ ờ ạ
v i m t đt là 60ớ ặ ấ 0. Tính chi u cao c a c t c (làm tròn đn cm).ề ủ ộ ờ ế
Bài 4 : (3,5 đi m)ể
Cho tam giác ABC vuông t i A, k đng cao AH. T H k HE vuông góc AB (Eạ ẻ ườ ừ ẻ
thu c AB), k HF vuông góc AC (F thu c AC).ộ ẻ ộ
a) Ch ng minh r ng : AE . AB = AF . AC.ứ ằ
b) Khi AB = 5cm; AH = 4cm. Tính s đo góc HAC.ố
c) V trung tuy n AM c a tam giác ABC. Ch ng minh: ẽ ế ủ ứ
ﾷ
sin 2sinC.sinBAMB =
.
Đ 2:ề
Bài 1 : (2 đi m)ể
Cho tam giác ABC vuông t i A, k đng cao AH, bi t BH = 1, AH = 3. Tính đạ ẻ ườ ế ộ
dài CH.
Bài 2 : (3 đi m)ể
S p x p các t s l ng giác sau theo th t tăng d n:ắ ế ỉ ố ượ ứ ự ầ
tan240 , cot350 , tan540 , cot700 , tan780 , cot450.
Bài 3 : (1,5 đi m)ể
M t cây cau có bóng n ng trên m t đt dài 14m. Bi t góc mà tia sáng m t tr i t oộ ắ ặ ấ ế ặ ờ ạ
v i m t đt là 55ớ ặ ấ 0. Tính chi u cao c a cây cau (làm tròn đn cm).ề ủ ế
Bài 4 : (3,5 đi m)ể
Cho tam giác ABC vuông t i A, k đng cao AH. T H k HE vuông góc AB (Eạ ẻ ườ ừ ẻ
thu c AB), k HF vuông góc AC (F thu c AC).ộ ẻ ộ
a) Ch ng minh r ng : ứ ằ
AE AC
AF AB
=
.
b) Khi AB = 10cm; AH = 8cm. Tính s đo góc C.ố
c) V trung tuy n AM c a tam giác ABC. Ch ng minh: ẽ ế ủ ứ
ﾷ
sin 2.cosC.cos BAMB =
.
V. H NG D N CH M BÀI KI M TRAƯỚ Ẫ Ấ Ể
Đ 1:ề
Bài Câu N i dung ch mộ ấ Đi mể
chi ti tế
T ngổ
số
đi mể
1
+ Hình v đúngẽ
+ AH2 = BH.CH = 4.9 = 36
⇒ AH = 6
0,5
1
0,5
2
2
cos350 = sin550 ; cos700 = sin200 ; cos450= sin450
Vì 200 < 240 < 450 < 540 < 550 < 780
sin200 < sin240 < sin450 < sin540 < sin550 < sin780
cos700 < sin240 < cos450 <sin540 < cos350 < sin780
1
1
1
3
3
+ Hình v đúngẽ
+ Tính đúng : chi u cao cây : 4.tan60ề0 = 6,93(m)
0,5
1
1,5
4 a + Hình vẽ
M
Áp d ng h th c l ng cho ụ ệ ứ ượ AHB và AHC
AH2 = AE.AB; AH2 = AF.AC
+ Suy ra : AE.AB = AF.AC
0,5
3,5
1
b
4
5
AH
sinB AB
= =
ﾷ
B =
530 8’
Mà
ﾷ
ﾷ
HAC B=
(cùng ph ụ
ﾷ
HAB
), nên
0,5
0,5
c
Ta có
2sinC.sinB 2sinC.cosC 2 .
AH CH
AC AC
= =
ﾷ
2
2 . 2 . 2 sin
. 2
AH CH AH CH AH AH AMB
AC BC CH AM AM
= = = = =
V y ậ
ﾷ
sin 2sinC.sinBAMB =
0,5
0,5
Đ 2:ề
Bài Câu N i dung ch mộ ấ Đi mể
chi ti tế
T ngổ
số
đi mể
1
+ Hình v đúngẽ
+ AH2 = BH.CH => 32= 1.CH
⇒ CH = 9
0,5
1
0,5
2
2
cot350 = tan550 ; cot700 = tan200 ; cot450= tan450
Vì 200 < 240 < 450 < 540 < 550 < 780
tan200 < tan240 < tan450 < tan540 < tan550 < tan780
cot700 < tan240 < cot450 <tan540 < cot350 < tan780
1
1
1
3
3
+ Hình v đúngẽ
+ Tính đúng : chi u cao cây : 14.tan55ề0 = 19,99(m)
0,5
1
1,5
4 a + Hình vẽ
M
3,5
Áp d ng h th c l ng cho ụ ệ ứ ượ AHB và AHC
AH2 = AE.AB; AH2 = AF.AC
+ Suy ra : AE.AB = AF.AC
AE AC
AF AB
=
0,5
1
b
8
10
AH
sinB AB
= =
ﾷ
B =
530 8’
Mà
ﾷ
ﾷ
0
90C B+ =
nên
ﾷ
0
36 52'C=
0,5
0,5
c
Ta có
2cosC.cosB 2cosC.sinC 2 .
AH CH
AC AC
= =
ﾷ
2
2 . 2 . 2 sin
. 2
AH CH AH CH AH AH AMB
AC BC CH AM AM
= = = = =
V y ậ
ﾷ
sin 2cosC.cosBAMB =
0,5
0,5