Trang 1/6 - Mã đề thi 132
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT HẬU LỘC 2
( Đề thi gồm có 06 trang)
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1
Môn: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Ngày thi: 12/01/2020
Mã đề thi
132
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Cho cấp số nhân
()
n
u
có số hạng đầu
13u
và
212u
. Công bội của cấp số nhân đó là
A.
4
. B.
9
. C.
36
. D.
1
4
.
Câu 2: Nghiệm của phương trình
3
log ( 1) 4x
là
A.
65x
. B.
81x
. C.
82x
. D.
64x
.
Câu 3: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ): (x 1) (y 2) (z 1) 4.S
Tọa độ tâm
I
và bán
kính
R
của mặt cầu
()S
là
A.
(1;2; 1); R 2I
. B.
(1;2; 1); R 4I
.
C.
( 1; 2;1); R 4I
. D.
( 1; 2;1); R 2I
.
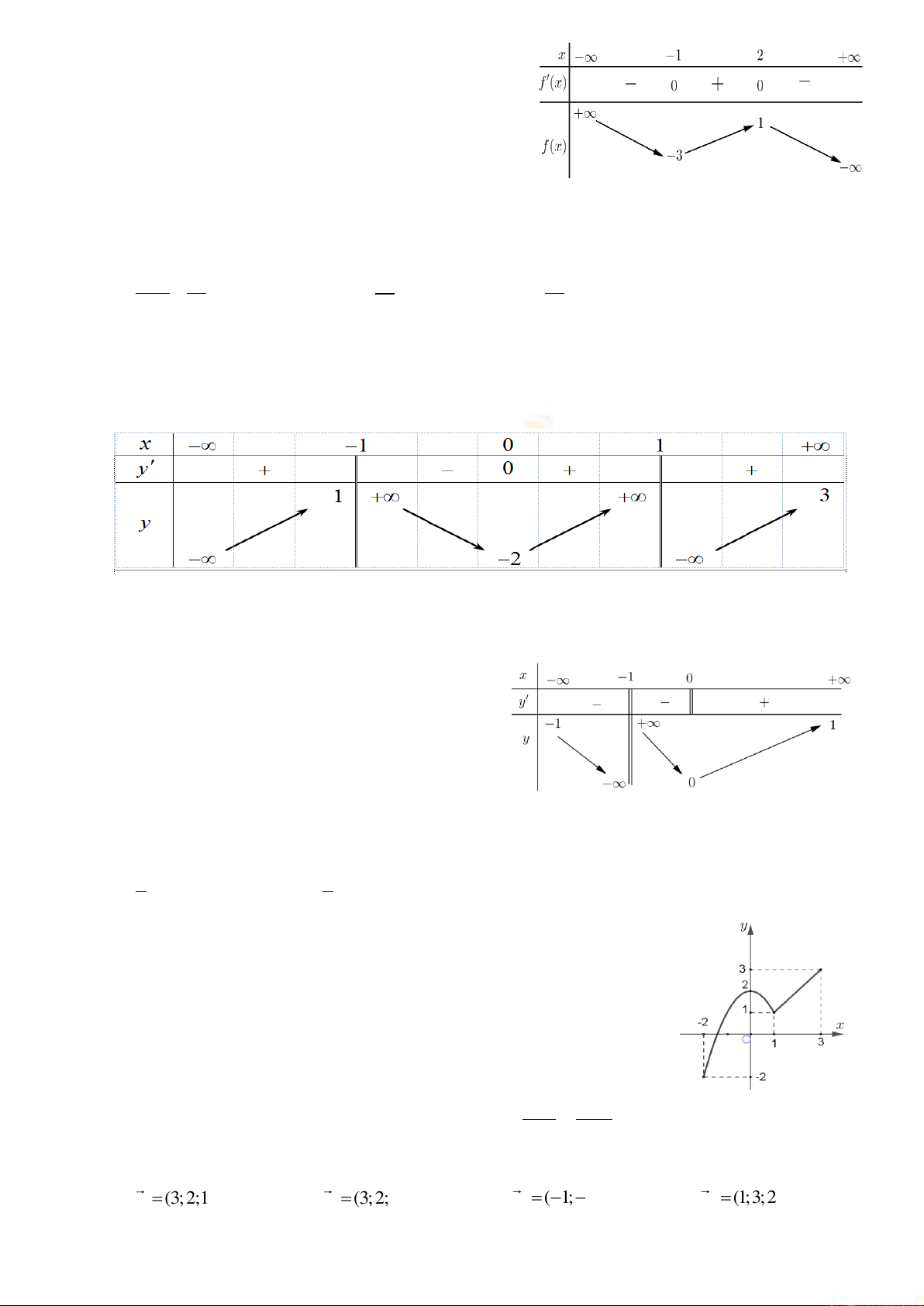
Câu 4: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
1x
. C.
0x
. D.
1x
.
Câu 5: Thể tích khối chóp có diện tích đáy
B
và chiều cao
h
là
A.
1
3Bh
. B.
Bh
. C.
1
3Bh
. D.
2
1
3Bh
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
( ): 2 1 0P x y
. Vectơ nào dưới đây là một vectơ
pháp tuyến của
P
?
A.
12;0; 1n
. B.
42; 1;1n
. C.
32; 1;0n
. D.
22;1; 1n
.
Câu 7: Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
(2;1; 3)M
lên mặt phẳng
()Oyz
có tọa
độ là
A.
(2;0;0)
. B.
(0;1; 3)
. C.
(2;1;0)
. D.
(2;0; 3)
.
Câu 8: Cho đa giác gồm 10 đỉnh. Số tam giác có ba đỉnh là ba trong số 10 đỉnh của đa giác là
A.
10
3
. B.
3
10
. C.
3
10
A
. D.
3
10
C
.
Câu 9: Cho hàm số
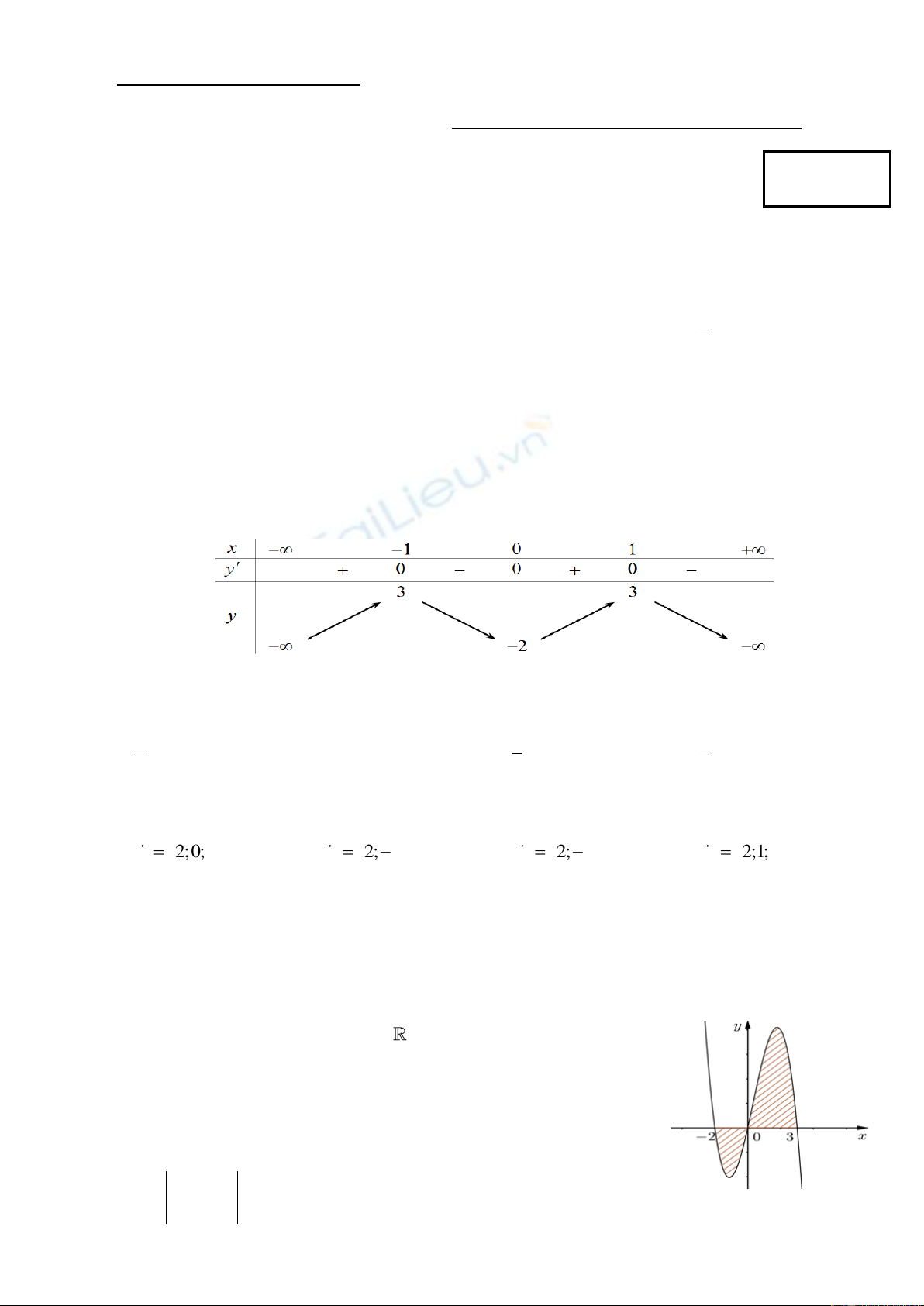
fx
liên tục trên . Gọi
S
là diện tích hình phẳng
giới hạn bởi các đường
( ), 0, 2y f x y x
và
3x
(như hình vẽ bên).
Mệnh đề nào dưới đây là đúng?
A.
00
23
( )d ( )dS f x x f x x


. B.
23
00
( )d ( )dS f x x f x x


.
C.
3
2
( )dS f x x
. D.
03
20
( )d ( )dS f x x f x x


.
Trang 2/6 - Mã đề thi 132
Câu 10: Cho hàm số
()y f x
có bảng biến thiên như
hình vẽ bên. Khẳng định nào sau đây là đúng?
A. Hàm số
()fx
nghịch biến trên
( ; 1) (2; ) 
.
B. Hàm số
()fx
nghịch biến trên khoảng
( ; 3)
.
C. Hàm số
()fx
đồng biến trên khoảng
( 3;1)
.
D. Hàm số
()fx
đồng biến trên khoảng
(2; )
.
Câu 11: Họ nguyên hàm của hàm số
() x
f x e x
là
A.
12
12
x
ex
C
x

. B.
2
1
2
xx
xe C

. C.
2
2
xx
eC
. D.
1
x
eC
.
Câu 12: Cho
2
0
( ) 2f x dx
và
0
2
g( ) 1x dx
, khi đó
2
0
[ ( ) 3g( )]f x x dx
bằng
A.
3
. B.
1
. C.
5
. D.
1
.
Câu 13: Cho hàm số
()y f x
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 14: Cho hàm số
y f x
có bảng biến thiên
như hình bên. Số nghiệm thực của phương trình
2 1 0fx
là
A.
0
. B.
3
.
C.
2
. D.
1
.
Câu 15: Khối cầu có bán kính bằng
a
có thể tích là
A.
3
4
3a
. B.
2
4
3a
. C.
3
a
. D.
2
4a
.
Câu 16: Cho hàm số
y f x
liên tục trên đoạn
2;3
và có đồ thị
như hình vẽ bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất
của hàm số đã cho trên đoạn
2;3 .
Giá trị của
Mm
bằng
A.
5
. B.
1
.
C.
3
. D.
1
.
Câu 17: Trong không gian
Oxyz
, cho đường thẳng
d
:
132
32
xyz

. Vectơ nào dưới đây là một
vectơ chỉ phương của đường thẳng (d)?
A.
1(3;2;1)u
. B.
2(3;2;0)u
. C.
3( 1; 3; 2)u
. D.
4(1;3;2)u
.
Trang 3/6 - Mã đề thi 132
Câu 18: Với
a
là số thực khác không tùy ý,
2
3
log a
bằng
A.
3
1log
2a
. B.
3
1log
2a
C.
3
2log a
. D.
3
2log a
.
Câu 19: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
33y x x
. B.
42
2.y x x
C.
42
2.y x x
D.
33y x x
.
Câu 20: Hàm số
3x
y
có đạo hàm là
A.
3
ln3
x
. B.
3 ln3
x
. C.
3 ln3
x
. D.
1
3x
x
.
Câu 21: Số phức liên hợp của số phức
23i
là
A.
23i
. B.
23i
. C.
23i
. D.
32i
.
Câu 22: Trong không gian
Oxyz
, cho điểm
(1;3;2)A
. Gọi
,,M N P
lần lượt là hình chiếu của
A
lên các
trục
,,Ox Oy Oz
. Phương trình mặt phẳng
()MNP
là
A.
3 2 14 0x y z
. B.
6 3 2 6 0x y z
.
C.
0
1 3 2
x y z
. D.
6 2 3 6 0x y z
.
Câu 23: Gọi
12
, zz
là hai nghiệm phức của phương trình
22 3 0zz
. Giá trị
12
zz
bằng
A.
6
B.
2
C.
3
D.
23
.
Câu 24: Thể tích của khối nón có độ dài đường sinh
5l
và bán kính đáy
3r
là
A.
20
. B.
12
. C.
36
. D.
60
.
Câu 25: Trong hình vẽ bên điểm
M
là điểm biểu diễn số phức
1zi
. Điểm biểu diễn số phức
z
là
A. Điểm
C
. B. Điểm
A
.
C. Điểm
D
. D. Điểm
B
.
Câu 26: Cho hình lập phương
.ABCD A B C D
. Góc giữa hai đường thẳng
AC
và
AB
bằng
A.
0
60
. B.
0
45
. C.
0
90
. D.
0
30
.
Câu 27: Biết rằng
,ab
là những số thực để phương trình
9 .3 0
xx
ab
luôn có
2
nghiệm thực phân
biệt
12
,.xx
Khi đó tổng
12
xx
bằng
A.
b
. B.
3
log .a
C.
a
. D.
3
log .b
Câu 28: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng
a
. Thể tích của khối lăng trụ là
A.
33
4
a
. B.
33
12
a
. C.
33
2
a
. D.
33
6
a
.
Câu 29: Cho hàm số
fx
có đạo hàm
23 .' 1 2 ,f x x x x x
Số điểm cực trị của hàm số đã
cho là
A.
6
. B.
2
. C.
1
. D.
3
.
Câu 30: Cho
a
và
b
là hai số thực dương thỏa mãn
24
log 5 log 5
4, 2ab
. Giá trị của
22
24
log 5 log 5
5ab
bằng
A.
150
. B.
30
. C.
25 5
. D.
25 5 5
.
2
x
y
2
1
1
Trang 4/6 - Mã đề thi 132
Câu 31: Cho hàm số
()y f x
có đồ thị hàm đạo hàm
()y f x
như
hình bên. Hàm số
( ) (2019 2020 )g x f x
đồng biến trên khoảng nào
trong các khoảng sau?
A.
( 1;0)
. B.
( ; 1)
.
C.
(0;1)
. D.
(1; )
.
Câu 32: Họ nguyên hàm của hàm số
1
( ) 2 x
f x xe
là
A.
1
2( 1) x
x e C

. B.
1
( 1) x
x e C

. C.
1
(2 1) x
x e C

. D.
1
1( 1)
2
x
x e C

.
Câu 33: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 2 4 2 0S x y z x y z
và điểm
1;1; 1A
. Ba mặt phẳng thay đổi đi qua
A
và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường
tròn. Tổng diện tích của ba hình tròn tương ứng là
A.
. B.
11
. C.
10
. D.
4
.
Câu 34: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
log (9 ) 1
xmx
có hai nghiệm
thực phân biệt?
A.
4
. B.
2
. C. Vô số. D.
3
.
Câu 35: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
2 2 2AD AB BC a
,
SA
vuông góc với đáy, góc giữa
SB
và mặt đáy bằng
0
60
. Gọi
H
là hình chiếu
của A lên
SB
. Khoảng cách từ
H
đến mặt phẳng
()SCD
bằng
A.
3a
. B.
3 30
20
a
. C.
30
10
a
. D.
3 30
40
a
.
Câu 36: Một hộp đựng
15
tấm thẻ được đánh số từ
1
đến
15
. Chọn ngẫu nhiên 6 tấm thẻ trong hộp. Xác
suất để tổng các số ghi trên
6
tấm thẻ được chọn là một số lẻ bằng
A.
71
143
. B.
56
715
. C.
72
143
. D.
56
143
.
Câu 37: Cho hàm số
y f x
, hàm số
y f x
liên tục trên và có
đồ thị như hình vẽ bên. Bất phương trình
x
m fex
có nghiệm với
mọi
1;1x
khi và chỉ khi
A.
1
min 1 ; 1 .m f e f e



B.
0 1.mf
C.
1
min 1 ; 1 .m f e f e



D.
01mf
.
Câu 38:
Một chiếc cốc hình trụ có bán kính lòng t
rong
đáy
10R cm
, trong cốc chứa nước có chiều cao
4h cm
. Người ta bỏ vào cốc một viên bi hình cầu
bằng kim loại, lúc này mặt nước trong cốc dâng lên
vừa phủ kín viên bi (tham khảo hình vẽ). Bán kính của
viên bi gần nhất với kết quả nào dưới đây?
A.
2,06cm
. B.
4,31cm
.
C.
11.09cm
. D.
2cm
.
Trang 5/6 - Mã đề thi 132
Câu 39: Trong không gian
Oxyz
, cho ba điểm
1;0;0 , 0;2;0 , 0;0;3A B C
. Gọi
H
là trực tâm tam
giác
ABC
. Đường thẳng
OH
có phương trình là
A.
1 2 3
6 3 2
x y z

. B.
1 2 3
x y z

.
C.
6 3 2
x y z

. D.
1
1 2 3
x y z
.
Câu 40: Cho hàm số
y f x
thỏa mãn
2
0
sin . d 2x f x x
, biết
2
0
cos . d 1I x f x x

. Giá trị
0f
là
A.
1
. B.
2
C.
3
. D.
1
.
Câu 41: Cho số phức
z
thỏa mãn
50z i z i
. Môđun của
z
bằng
A.
13
. B.
169
. C.
7
. D.
49
.
Câu 42: Cho hàm số
32
( ) ( , , , )y f x ax bx cx d a b c d
có đồ thị như hình vẽ bên. Số nghiệm của phương trình
( ) ( ) 2 ( ) (1) 0f f f x f x f x f
là
A.
2
. B.
3
.
C.
1
. D.
0
.
Câu 43: Cho hàm số
2
223
()
3
x x m x m
yC
x
và đường thẳng
( ): 2d y x
(
m
là tham số thực).
Số giá trị nguyên của
15;15m
để đường thẳng
()d
cắt đồ thị
()C
tại bốn điểm phân biệt là
A.
15
. B.
30
. C.
16
. D.
17
.
Câu 44: Cho hàm số
()y f x
có đồ thị trên đoạn
[ 2;6]
như hình
vẽ bên. Biết các miền
,,A B C
có diện tích lần lượt là
32, 2
và
3
.
Tích phân
22
2
3
(3 4) 1 2 5
4
I x f x x dx






bằng
A.
1
2
I
B.
82I
.
C.
66I
. D.
50I
.
Câu 45: Cho phương trình
10 log( ) 2log( 1) 0
x
me x m mx x
(
m
là tham số). Có tất cả bao
nhiêu giá trị nguyên của
m
để phương trình đã cho có ba nghiệm thực phân biệt?
A. Vô số. B.
11
. C.
10
. D.
5
.
Câu 46: Cho hàm số
()fx
có đạo hàm cấp hai trên đoạn
0;1
đồng thời thỏa mãn các điều kiện
(0) 1, ( ) 0f f x

và
2
( ) ( ) , 0;1f x f x x
. Giá trị
(0) (1)ff
thuộc khoảng
A.
(1;2)
. B.
( 1;0)
. C.
(0;1)
. D.
( 2; 1)
.
Câu 47: Giả sử
12
,zz
là hai trong số các số phức
z
thỏa mãn
21iz i
và
12
2zz
Giá trị lớn
nhất của
12
zz
bằng
A.
3
. B.
32
. C.
4
. D.
23
.