UBND HUYỆN LONG ĐIỀN
TRƯỜNG THCS NGUYỄN THỊ ĐỊNH
ĐỀ CHÍNH THỨC
(Đề thi gồm 01 trang)
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT
NĂM HỌC 2022 – 2023
MÔN THI: TOÁN
Thời gian làm bài: 120 phút
Ngày thi: 22/04/2022
Bài 1: (3,5 điểm)
a) Giải phương trình: 2320xx
b) Giải hệ phương trình: 23 5
34 18
xy
xy
ì-=-
ï
ï
í
ï+=
ï
î
c) Rút gọn biểu thức :

2
6
A2375
23

d) Giải phương trình: 2
x 5 x 10x 2x 1
Bài 2: (2,0 điểm)
Cho parabol (P): 2
yx và đường thẳng (d): 2ymxm
(Với m là tham số)
a) Vẽ (P) và đường thẳng (d) trên cùng một hệ trục tọa độ khi m=1.
b) Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt parabol (P) tại hai điểm
phân biệt có hoành độ 12
,
x
x thỏa mãn 12
1xx
Bài 3: (0,5 điểm)
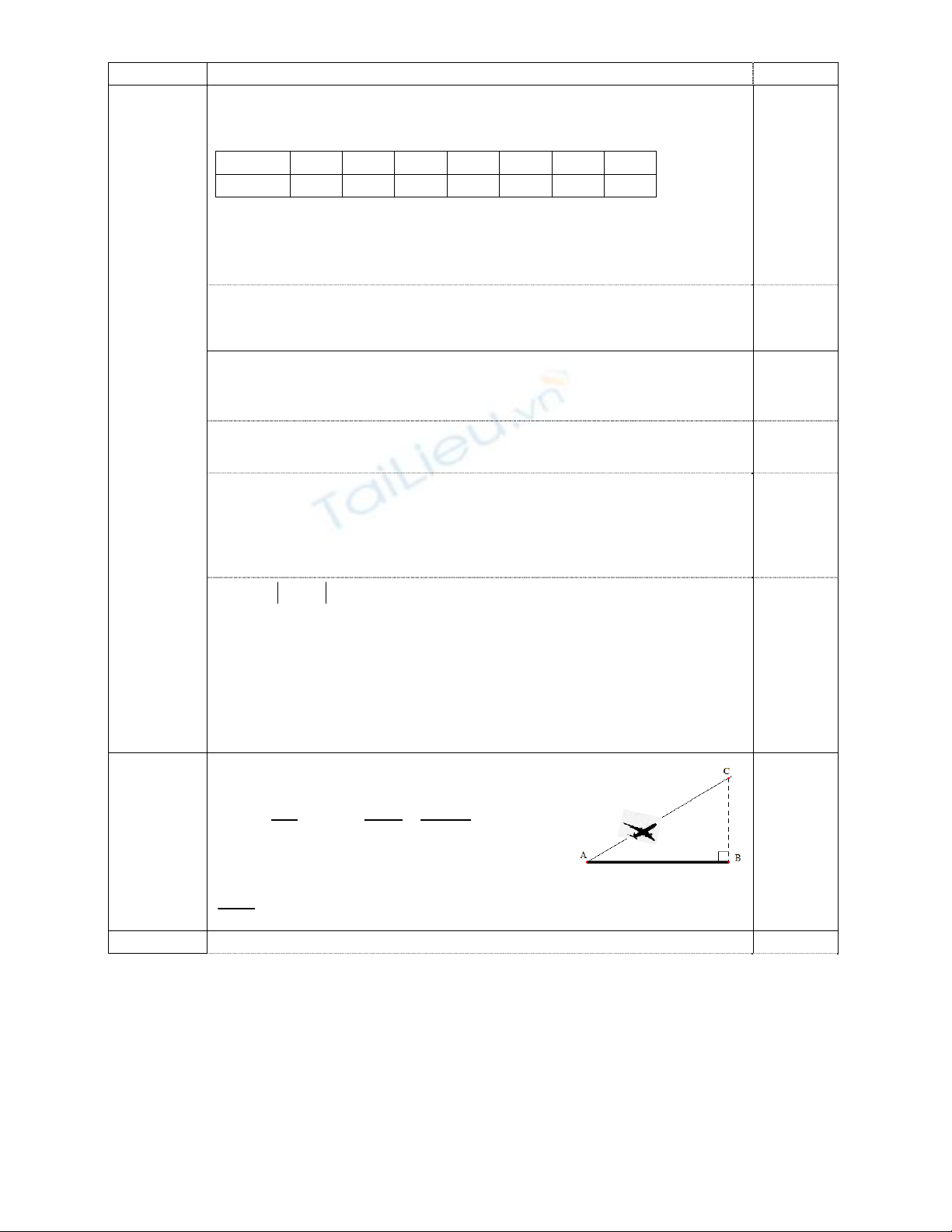
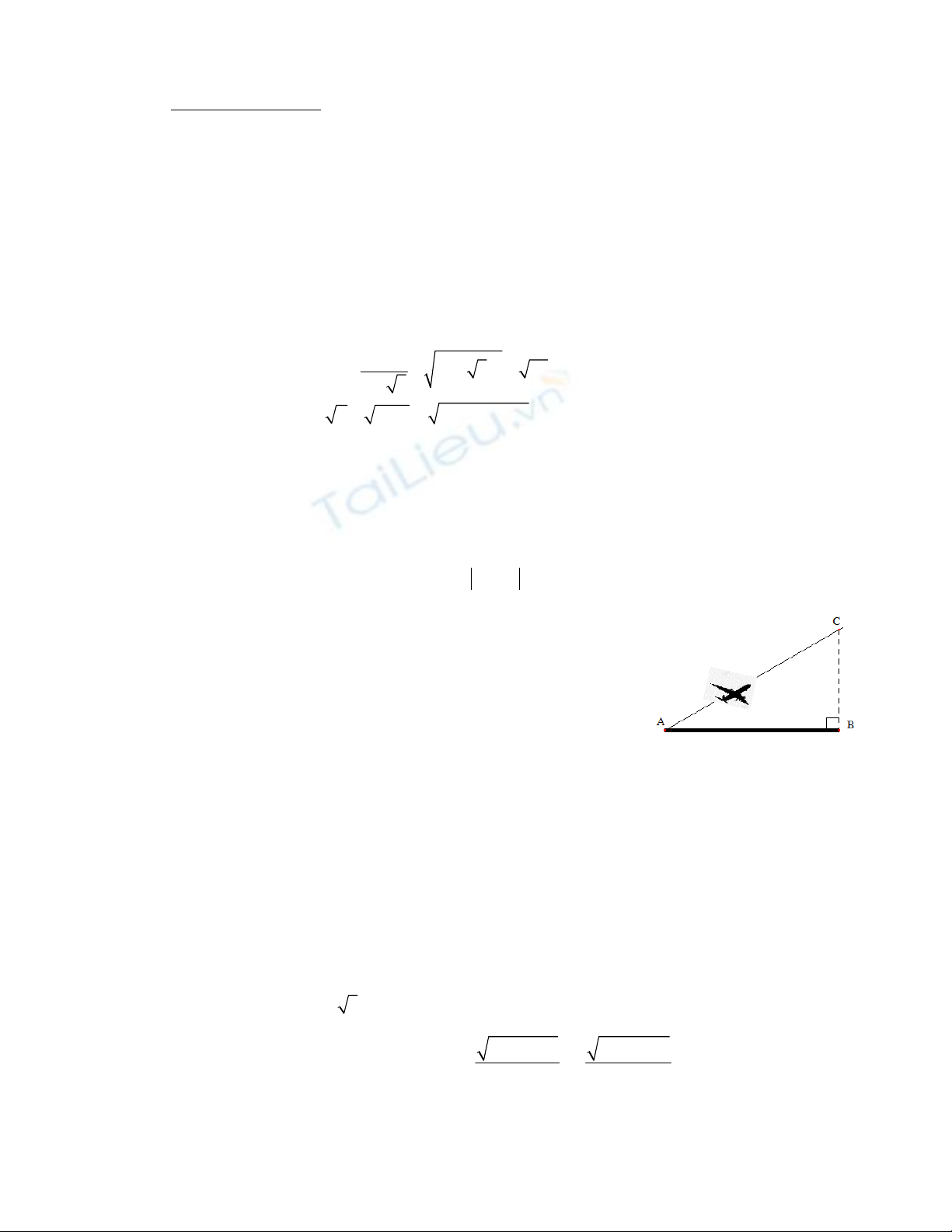
Một máy bay phản lực cất cánh từ vị trí A ( như hình vẽ )
bay lên với một góc 300 so với đường băng có phương nằm
ngang, sau một thời gian 30 giây máy bay đạt được độ cao
3000 mét so với đường băng. Tính vận tốc trung bình của
máy bay trong trường hợp này (làm tròn đến hàng đơn vị).
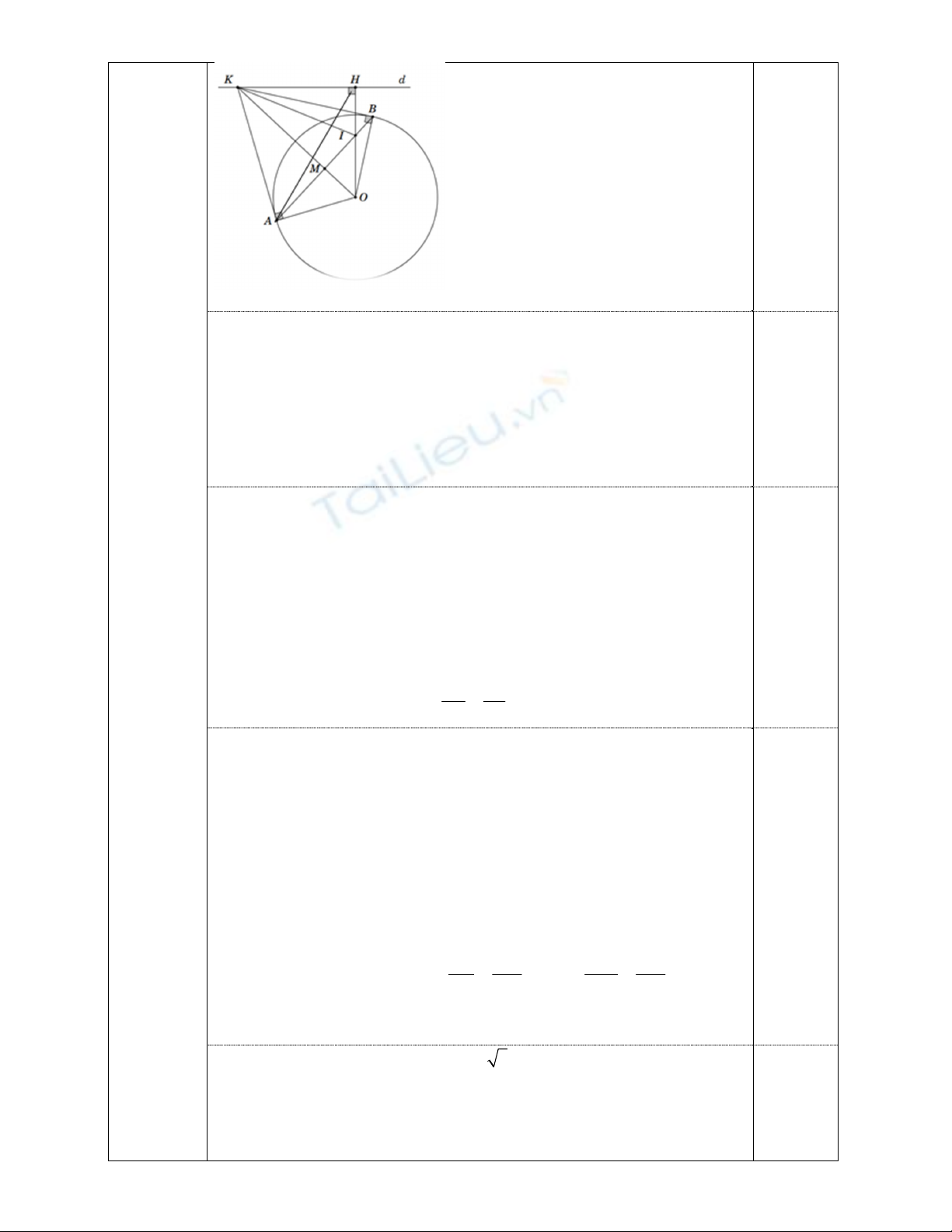
Bài 4:(3,5 điểm)Cho đường tròn tâm O, bán kính
R
và một đường thẳng d không cắt
đường tròn ()O. Dựng đường thẳng OH vuông góc với đường thẳng d tại điểm H. Trên
đường thẳng d lấy điểm K (khác điểm H), qua K vẽ hai tiếp tuyến KA và KB với đường
tròn ()O, (
A
và
B
là các tiếp điểm) sao cho
A
và Hnằm về hai phía của đường thẳng OK
a) Chứng minh tứ giác
K
AOH là tứ giác nội tiếp.
b) Đường thẳng AB cắt đường thẳng OH tại điểm I. Chứng minh rằng
I
AIB IH IO
c) Chứng minh Ilà điểm cố định khi điểm K chạy trên đường thẳng d cố định.
d) Khi 2, 3OK R OH R. Tính diện tích tam giác KAI theo
R
.
Bài 5: (0,5 điểm)Tìm giá trị lớn nhất của A = 2021 2022
11


xx
xx
.
‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐Hết-‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐‐
UBND HUYỆN LONG ĐIỀN
TRƯỜNG THCS NGUYỄN THỊ ĐỊNH
ĐÁP ÁN ĐỀ THI THỬ TS LỚP 10 NH 2022 – 2023
MÔN: TOÁN
( Thời gian làm bài 120 phút )
Câu Nội dun
g
Điểm
1
(3.5điểm)
a) (0.75 điểm)
2320xx
Lập: 1 (hoặc:0abc)
0.25
Phương trình có hai nghiệm: 12
1; 2xx
0.25x2
b) (0,75 điểm)
17 51
23 5 69 15
35
3 4 18 6 8 36
2
32.
3.3 5 3
2
y
xy xy y
xy xy x
yx
y
x
ì=
ï
ìì ï
-=- -=-
ïï ï
ïï

íí í
-
ïï ï
+= += =
ïï ïîî ï
î
ì=
ïì
ï=
ï
ïï

íí
-
ïï
=
=ï
ïî
ï
î
Vậy hệ phương trình có nghiệm duy nhất:
()
()
;2;3.xy =
(
N
ế
u học sinh ch
g
hi k
ế
t quả đún
g
thì ch
đư
ợ
c 0.25 đi
ể
m)
0.25
0.25x2
c) (1điểm)

2
6
A2375
23

=
62 3 2353
43

12 6 3 2 3 5 3 14
0.25x2
0.25x2
d) (1 điểm)
2
x 5 x 10x 2x 1
ĐKXĐ: 0x5

2
22
x 5 x 10x 2x 1
x 2 x(5 x) 5 x 2x(5 x) 1 
2x(5 x) 2 x(5 x) 4 0
x(5 x) x(5 x) 2 0
(1)
Đặt tx(5x)
( t0)
2
tx(x5)
(1) t2 – t – 2 = 0 (*)
Ta có: a - b + c = 1 – (-1) + (-2) = 0
Nên pt (*) có 2 nghiệm là t1 = -1 ( loại);
t2 = c2
a
( nhận)
Với t = 2, ta có: 22 = x(5 - x) x2 – 5x + 4 = 0 (**)
Ta có: a + b + c = 1 + (-5) + 4 = 0
Nên pt (**) có hai nghiệm x1 = 1 ( nhận);
x2= c4
a( nhận)
Vậy pt(1) có hai nghiệm là 1; 4.
0.25
0.25
0.25
0.25
Lưu
ý
: Hs làm cách khác cho k
ế
t quả đún
g
thì t
r
ọn đi
ể
m
2
(2.0điểm)
a) (1.0điểm)
* y= x2
Bảng giá trị
x -3 -2 -1 0 1 2 3
y = x2 9 4 1 0 1 4 9
* y = mx – m +2
Với m = 1 thì: y = x + 1
Cho x= 0 thì y = 1 ta được (0;1)
y
= 0 thì x = -1 ta được (-1; 0)
0.25
0.25
Đồ thị: (cả hai đồ thị chính xác)
Hs vẽ đồ thị đúng mỗi đồ thị được 0,25 điểm, trục tọa độ thiếu 2
tron
g
3 tên O, x,
y
thì khôn
g
cho đi
ể
m.
0.5
b) (1.0điểm)
Phương trình hoành độ giao điểm của (P) và (d) là:
22
220mx m mx m
x
x
0.25
(d) cắt (p) tại hai điểm phân biệt 2
0( 2)40m
) (đúng m R
0.25
12
,
xVì x là hai nghiệm của phương trình hoành độ giao điểm nên
theo hệ thức Vi-et ta có:
12
12
.2
x
xm
xx m


0.25
2
12 12
2
12 12
22
1( )1
()41
4( 2) 0
:
17
4
xx xx
xx xx
Khi đó
mm mm


 
Phương trình này vô nghiệm. Vậy không tìm được giá trị nào của m
thõa mãn điều kiện đề bài.
0.25
3
(0,5 điểm)
ABCvuông tại B, có:
0
BC BC 3000
SinA AC 6000
AC SinA Sin30
 m
vận tốc trung bình của máy bay trong trường
hợp này là:
6000 200
30 m/s
0.25
0.25
4 Hình vẽ (Vẽ hình chỉ để c/m câu a thì được 0.25 đ) 0.5
(3.5 điểm)
a) (1 điểm) Chứng minh tứ giác KAOH là tứ giác nội tiếp.
Tứ giác KAOH có:
90 KAO
(KA là tiếp tuyến)
90 ( )
K
HO OH KH


180KAO KBO

Mà hai góc này đối nhau
Nên tứ giác KAOH nội tiếp đường tròn đường kính OK
0.25
0.25
0.25
0.25
b)(0,75 điểm) Chứng minh rằng IA IB IH IO
Tứ giác KAOH nội tiếp đường tròn đường kính OK (cmt)
Mà KBOvuông tại B (KB là tiếp tuyến)
,,KBO
thuộc đường tròn
đường kính OK
Vậy năm điểm
,,,,KABOH
cùng thuộc đường tròn đường kính OK
Xét
IAH
và
IOB có:
HIA BIO
(đối đỉnh)
AHI ABO
(hai góc nội tiếp cùng chắn cung AO ).
Do đó
(.) IA IO
IAH IOB g g IA IB IH IO
IH IB

∽
.
0.25
0.25x2
c) (0,75 điểm) Chứng minh
I
là điểm cố định khi điểm
K
chạy
trên đường thẳng d cố định
Xét tứ giác AOBH nội tiếp có:
OHB
là góc nội tiếp chắn cung OB
OBA
là góc nội tiếp chắn cung OA
Mà OA OB R
nên
OHB OBA
.
Xét OIB và OBH có :
BOH
góc chung
OHB OBA
(cmt).
Do đó
22
(.) OI OB OB R
OIB OBH g g OI
OB OH OH OH

∽
.
Ta lại có đường thẳng d cố định nên OH không đổi (OH d).
Vậy điểm
I
cố định khi
K
chạy trên đường thẳng d cố định
0.25
0.25
0.25
d) (0,5 điểm) Khi 2, 3OK R OH R. Tính diện tích tam giác
KAI
theo
R
Gọi
M
là giao điểm của OK và AB
Theo tính chất hai tiếp tuyến cắt nhau ta có KA=KB;
Lại có OA OB R
nên OK là đường trung trực của AB, suy ra
A
BOK tại
M
và
M
AMB.
Theo câu b) ta có
22
33
RRR
OI OH R

.
Xét OAK vuông tại A, có
22
2
22
OA R R
OA OM OK OM OK R

Suy ra 3
222
R
R
KM OK OM R

2
233 3
22 4 2
RR R R
AM OM KM AM

Xét OMI vuông tại
M
, có
22
22 3
26
3
RRR
MI OI OM 






Suy ra 3323
26 3
RR R
AI AM MI

Diện tích
A
KI là 2
113233
22232
RR R
SAIKM
 .
0.25
0.25
5
(0,5 điểm) Tìm giá trị lớn nhất của A = 2021 2022
11


xx
xx
.
Đặt 2021ax ; 2022bx ( a, b 0)
2
2
2022 1
2021 1


ax
bx
Ta có: A = 22
2022 2021

ab
ab
2 2022 2 2021

ab
ab
11
2 2022 2 2021

max
11
2 2022 2 2021
A khi
2
2
2022
2021
a
b
2021 2022 4043
2022 2021



xx
x
Vậy GTLN của A là 11
2 2022 2 2021
khi x = 4043
0.25
0.25