1/7 - Mã đề 101
SỞ GD&ĐT NGHỆ AN
CỤM TRƯỜNG THPT
QUỲNH LƯU - HOÀNG MAI
YÊN THÀNH - THÁI HOÀ
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2022
Bài thi môn: Toán
Thời gian làm bài: 90 phút (50 câu trắc nghiệm)
Họ và tên học sinh :..................................................... Số báo danh : ...................
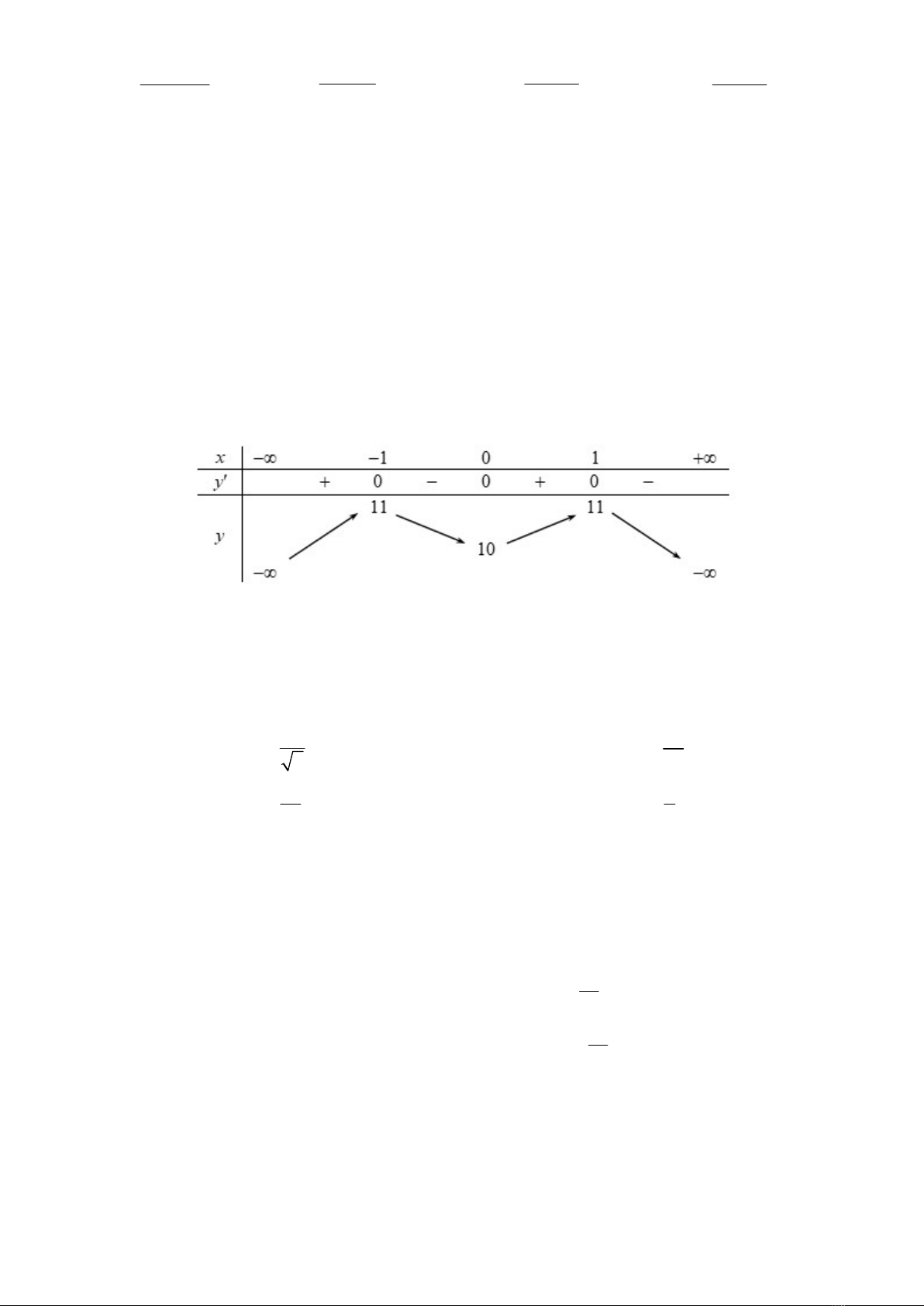
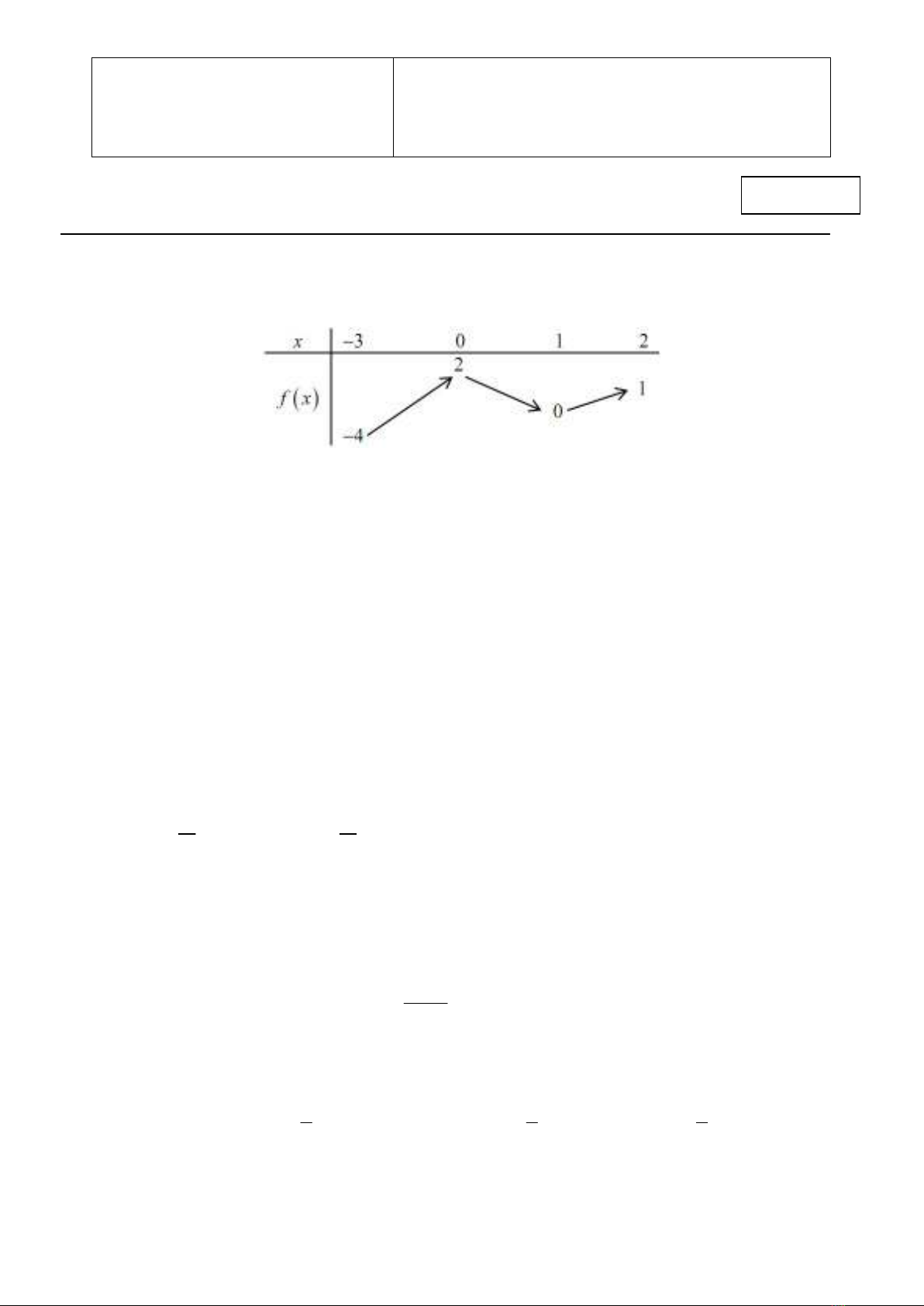
Câu 1. Cho hàm số
f x
liên tục trên
3;2
và có bảng biến thiên như hình vẽ. Gọi
,
lần lượt là giá
trị lớn nhất và nhỏ nhất của
f x
trên
3;2
. Tính 2
M m
?
A.
8
. B.
5
. C.
7
. D.
4
.
Câu 2. Trong không gian
Oxyz
, cho điểm
( 1;3;2)
M
. Đường thẳng đi qua
M
và song song
Ox
có
phương trình tham số là
A.
1
2
3
x t
y
z
B.
1
3
2
x t
y t
z t
. C.
1
3
2
x t
y
z
. D.
1
3
2
x t
y t
z t
.
Câu 3. Nghiệm của phương trình
log 3 1
x
là
A.
13
x
. B.
3
x
. C.
7
x
. D.
2
x
.
Câu 4. Cho số phức
4 5
z i
. Biểu diễn hình học của
z
là điểm có tọa độ
A.
4;5
. B.
4; 5
. C.
4; 5
. D.
4;5
.
Câu 5. Trong không gian với hệ trục
Oxyz
cho ba điểm
1;2; 3 , 1;0;2 , ; ; 2
A B C x y
thẳng hàng.
Khi đó
x y
bằng
A.
11
5
x y
. B.
11
5
x y . C.
17
x y
. D.
1
x y
.
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, mặt phẳng đi qua các điểm
2;0;0
A,
0;3;0
B,
0;0;4
C
có phương trình là
A.
6 4 3 12 0
x y z
. B.
6 4 3 24 0
x y z
.
C.
6 4 3 12 0
x y z
. D.
6 4 3 0
x y z
.
Câu 7. Tiệm cận ngang của đồ thị hàm số
1 2
1
x
y
x
A.
1.
x
B.
1.
y
C.
2.
y
D.
2.
y
Câu 8. Hàm số
2
log 3 2
y x
có tập xác định là:
A.
. B. 3;
2

. C.
3
;
2

. D. 3;
2
.
Câu 9. Với
n
là số nguyên dương bất kì,
3
n
, công thức nào dưới đây đúng?
Mã đề 101
2/7 - Mã đề 101
A.
3
!
3! 3 !
n
n
Cn
. B.
3
!
3 !
n
n
Cn
. C.
3
3!
3 !
n
Cn
. D.
3
3 !
!
n
n
C
n
.
Câu 10. Cho khối chóp tứ giác có thể tích
3
2
V a
, đáy là hình vuông có cạnh bằng
a
. Tính chiều cao khối
chóp.
A.
6
a
. B.
2
a
. C.
3
a
. D.
a
.
Câu 11. Cho
a
là số thực dương,
1
a
, khi đó
log 5
a
a bằng
A.
5
a
. B. 5
log
a
. C.
log 5
a
. D.
5
.
Câu 12. Có bao nhiêu cách chọn
5
cầu thủ từ
11
cầu thủ trong một đội bóng để thực hiện đá
5
quả luân lưu
11 m
, theo thứ tự quả thứ nhất đến quả thứ năm.
A.
5
10
C
. B.
5
11
C
. C.
5
11
A
. D. 2
11
.5!
A.
Câu 13. Cho
a
,
b
là hai số thực thỏa mãn
6 2 2
a i bi
, với
i
là đơn vị ảo. Giá trị của 2
a b
bằng:
A.
5
. B.
1
. C.
1
. D.
4
.
Câu 14. Cho hàm số
( )
y f x
xác định và liên tục trên
có bảng biến thiên như sau
Hàm số đạt cực tiểu tại
A.
1
x
. B.
1
x
. C.
0
x
. D.
10
x
.
Câu 15. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
: 2 3 0
P x y z
và điểm
1;1;0
I.
Phương trình mặt cầu tâm
I
và tiếp xúc với
P
là:
A.
2 2 2
5
1 1
6
x y z . B.
2 2 2
25
1 1
6
x y z .
C.
2 2 2
25
1 1
6
x y z . D.
2 2 2
5
1 1
6
x y z
.
Câu 16. Trong không gian với hệ trục tọa độ
Oxyz
, cho hai điểm
0;1; 2
A
và
3; 1;1
B. Tìm tọa độ
điểm M sao cho
3
AM AB
.
A.
9;5; 7
M
. B.
9; 5;7
M. C.
9;5;7
M. D.
9; 5; 5
M
.
Câu 17. Họ các nguyên hàm của hàm số
sin 21
f x x
là
A.
21cos 21
f x dx x C
. B.
1
cos21
21
f x dx x C
.
C.
21cos 21
f x dx x C
. D.
1cos21
21
f x dx x C
.
Câu 18. Cho số phức
2 3
z i
. Số phức liên hợp của
iz
bằng
A.
3 2 .
i
B.
3 2 .
i
C.
3 2 .
i
D.
3 2 .
i
Câu 19. Cho hàm số
( )
y f x
xác định, liên tục trên
và có bảng biến thiên dưới đây:
3/7 - Mã đề 101
y
y'
x
Số nghiệm của phương trình
2 ( ) 1
f x
là:
A.
2
B.
1
C.
3
D.
4
Câu 20. Diện tích xung quanh của hình nón có bán kính đáy
4
r
và chiều cao
3
h
bằng:
A.
20
. B.
75
. C.
15
. D.
45
.
Câu 21. Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên dưới.
Hàm số
y f x
nghịch biến trên khoảng nào?
A.
2;1
B.
; 2

C.
1;

D.
2;0
Câu 22. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
A. 4 2
2 3
y x x
. B. 3
2 3
y x x
. C. 4 2
2 2 3
y x x
. D.
3
1
x
y
x
.
Câu 23. Số nghiệm của phương trình
2
3 1
3
log 4 log 2 3 0
x x x
là
A.
1
. B.
2
. C.
0
. D.
3
.
4/7 - Mã đề 101
Câu 24. Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
z
thoả mãn
. 1
z z
là
A. Một đường thẳng. B. Một điểm.
C. Một đường tròn. D. Một elip.
Câu 25. Cho hàm số
3 2
f x ax bx cx d
, , ,a b c d
có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số
, , , ?
a b c d
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 26. Cho
,
a b
là các số dương thỏa mãn 3 3
4log 7log 2
a b
. Khẳng định nào sau đây là đúng?
A. 4 7
2
a b
. B.
4 7 9
a b
. C. 4 7
9
a b
. D.
4 7 2
a b
.
Câu 27. Với giá trị nào của tham số m thì phương trình 1
4 .2 2 0
x x
m m
có hai nghiệm
1 2
,
x x
với
1 2
,
x x
thỏa mãn 1 2
3
x x
?
A.
3
m
B.
1
m
. C.
2
m
. D.
4
m
.
Câu 28. Cho hàm số 3 2
y ax bx cx d
có đồ thị như hình vẽ.
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0
a b c d
. B.
0, 0, 0, 0
a b c d
.
C.
0, 0, 0, 0
a b c d
. D.
0, 0, 0, 0
a b c d
.
Câu 29. Trên đoạn
0;4
, hàm số 4 2
12 2
4
y x x m
đạt giá trị lớn nhất bằng
5
tại
x a
. Tính
m a
A.
31
. B.
25
. C.
25
. D.
33
.
Câu 30. Biết
2
0
2 ln 1 d .ln
x x x a b
, với
*
,
a b N
,
b
là số nguyên tố. Tính
6 7
a b
.
A.
25
. B.
39
. C.
33
. D.
42
.
Câu 31. Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 4
y x x m x
đồng biến trên
khoảng
2;

A.
;1

. B.
;4
 . C.
;1

. D.
;4
 .
Câu 32. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh
S
và tạo với trục của
N
một góc bằng
30
, ta
được thiết diện là tam giác
SAB
vuông và có diện tích bằng
2
4
a
. Chiều cao của hình nón bằng:
5/7 - Mã đề 101
A.
3
a
. B.
2 3
a
. C.
2 2
a. D.
2
a
.
Câu 33. Biết rằng phương trình: 2
3 3
log ( 2)log 3 1 0
x m x m
có hai nghiệm
1 2 1 2
; ( )
x x x x
thỏa mãn
1 2
27
x x
. Khi đó tổng
1 2
2
x x
bằng:
A. 6. B.
34
3
. C.
1
3
. D. 15.
Câu 34. Cho hình chóp đều .
S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
o
60
. Tính thể tích
của khối chóp .
S ABCD
theo
a
.
A.
3
6
.
12
a B.
3
6
.
6
a C.
3
6
.
2
a D.
3
3
.
6
a
Câu 35. Thiết diện qua trục của một hình trụ là hình vuông cạnh
2
a
. Gọi
1
S
và
2
S
lần lượt là diện tích xung
quanh, diện tích toàn phần của hình trụ. Ta có:
A.
1 2
2
S S
. B.
1 2
4 3
S S
. C.
1 2
3 2
S S
. D.
1 2
2 3
S S
.
Câu 36. Mặt phẳng
P
cắt mặt cầu có tâm
O
theo đường tròn có bán kính bằng
4 cm
và khoảng cách từ
O
đến
P
bằng
3 cm
. Thể tích của mặt cầu là:
A.
3
500
cm
3
. B.
3
100
cm
3
. C.
3
100 cm
. D.
3
500 cm
.
Câu 37. Biết
1
ln
2
1 ln
ex
dx a b
x x
, với ,a b
. Tính
a b
.
A.
2
3
. B.
1
. C.
3
4
. D.
1
2
.
Câu 38. Cho số phức
,z x yi x y
thỏa mãn
1 2 3 4
i z z i
. Tính giá trị của biểu thức
3 2
S x y
.
A.
10
S
B.
12
S
C.
13
S
D.
11
S
Câu 39. Gọi
S
là tập hợp các số tự nhiên có
6
chữ số được lập từ tập
0;1;2;3;.....;9
A. Chọn ngẫu nhiên
một số từ tập
S
. Biết xác suất để chọn được số tự nhiên có tích các chữ số bằng
1400
bằng
a
b
với
( , ; ,
a b a b
nguyên tố cùng nhau). Tính
a b
A.
37501
. B.
15007
. C.
1501
. D.
5007
.
Câu 40. Cho tứ diện
ABCD
có
2 2
AC CD DB a
. Gọi
H
và
K
lần lượt là hình chiếu vuông góc của
A
và
B
lên đường thẳng
CD
sao cho
, , ,
H C D K
theo thứ tự cách đều. Biết góc tạo bởi
AH
và
BK
bằng
60
. Thể tích khối tứ diện
ABCD
bằng:
A.
3
3
6
a. B.
3
3
8
a. C.
3
3
3
a. D.
3
3
4
a.
Câu 41. Trong giờ nghỉ giữa giờ môn Toán, bốn bạn An, Bình, Cường, Dũng cùng nói chuyện về chiều cao
của mỗi người.
- An nói: Tôi cao nhất
- Bình nói: Tôi không thể là thấp nhất.
- Cường nói: Tôi không cao bằng An nhưng cũng không phải là thấp nhất.
- Dũng nói: Thế thì tôi thấp nhất rồi!
Để xác định ai đúng ai sai, họ đã tiến hành đo tại chỗ, kết quả là chỉ có một người nói sai và không có bạn
nào có cùng chiều cao. Ai là người nói sai?
A. Dũng. B. Cường. C. Bình. D. An.