THPT HÓA CHÂU
Dạng thức 2:
Câu 1. Cho bất phương trình
a) là một nghiệm của bất phương trình (1).
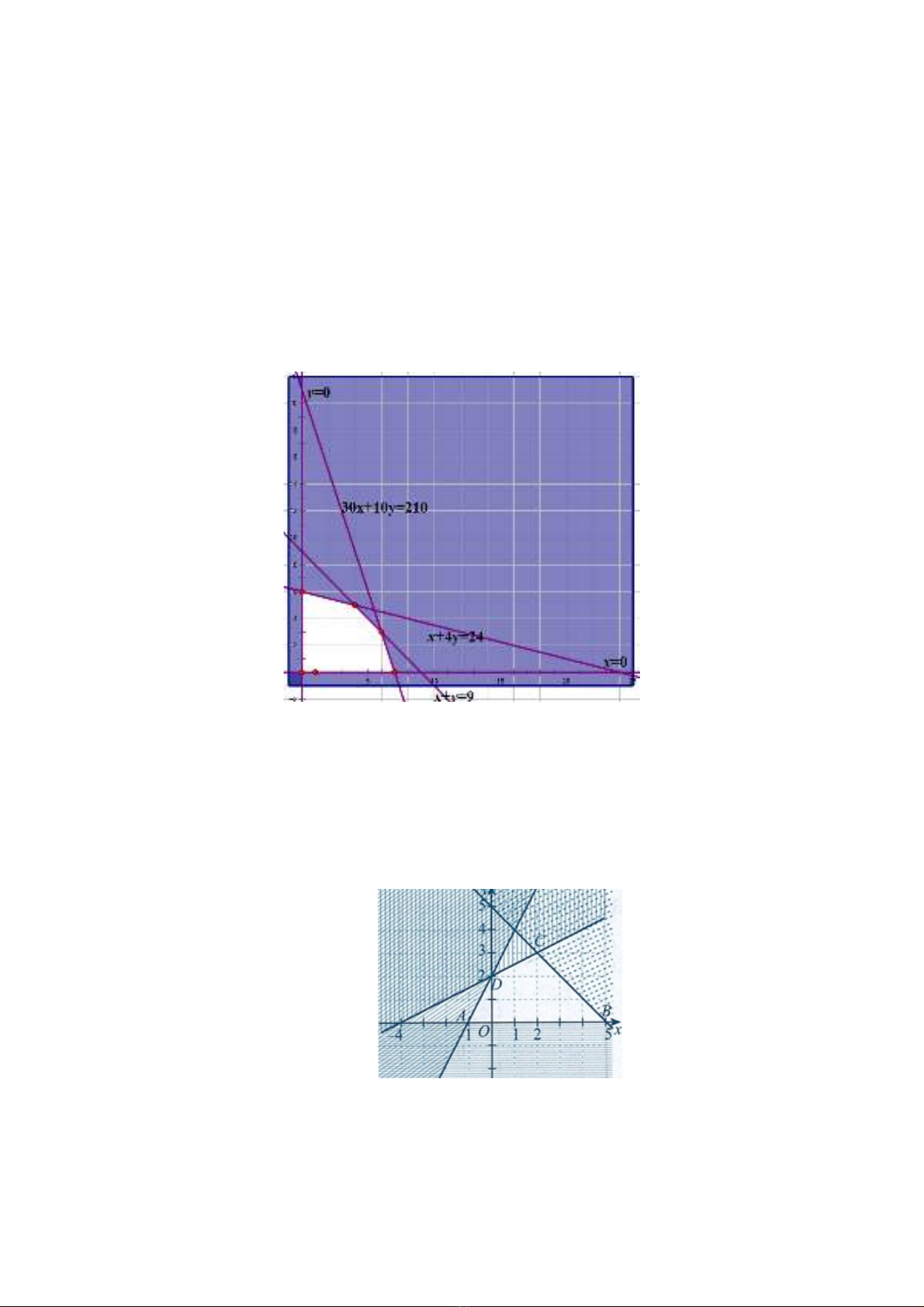
b)Miền nghiệm của bất phương trình (1) là miền nghiệm không tô đen ở hình bên (kể cảbờ đường thẳng )
.
c)Khi có hai giá trị thỏa mãn bất phương trình (1).
d) Có tất cả 6 nghiệm với thỏa mãn bất phương trình (1).
Lời giải
a) Vì đúng.
b) Đường thẳng chính là đường thẳng mà điểm thỏa mãn bất phương trình nên miền nghiệm chính là nửa
mặt phẳng đường thẳng có chứa điểm .
c) Khi vẽ đường thẳng thì có 2 giá trị là
d) Nghiệm với thỏa mãn bất phương trình (1) tức là thỏa mãn hệ bất phương trình và nên dựa vào miền
nghiệm của hệ bất phương trình ta được 7 nghiệm với thỏa mãn bất phương trình (1).
Câu 2: Cho bất phương trình:
a) là bất phương trình bậc nhất hai ẩn.
b) Cặp số (1;3) là nghiệm của bất phương trình.
c) Khi , với đều là nghiệm của bất phương trình.
d) Miền nghiệm của bất phương trình là nửa mặt phẳng bờ là đường thẳng chứa điểm
Lời giải
a) Đúng.
b) Đúng vì thay ta có
c) Thay vào ta có Suy ra khi thì đều là nghiệm của bất phương trình.
d) Thay vào ta có (sai).
Câu 3. An thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho An 200000 đồng để mua trái cây. Biết
rằng giá cam là 15000 đồng/1kg, giá xoài là 30000 đồng/1kg. Gọi lần lượt là số ki-lô-gam cam và xoài mà
An có thể mua về sử dụng trong một tuần. Các khẳng định sau đúng hay sai?
a) Trong tuần, số tiền An có thể mua cam là , số tiền An có thể mua xoài là
b) Bất phương trình bậc nhất cho hai ẩn là
c) Cặp số thỏa mãn bất phương trình bậc nhất cho hai ẩn
d) An có tất cả 18 cách để mua cam, xoài trong tuần với
Lời giải
a) Trong tuần, số tiền An có thể mua cam là , số tiền An có thể mua xoài là .
b) Ta có bất phương trình: .
c) Xét , thay vào bất phương trình: (đúng) nên là một nghiệm của (*).
d) Dựa vào hình biểu diễn của hệ bất phương trình ta thấy có 20 cặp số nguyên thỏa mãn hệ bất phương
trình.
Câu 4. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g
đường để pha chế nước cam và nước táo.
● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Gọi lần lượt là số lít nước cam, nước táo được tạo thành.
a) Biểu thức biểu diễn số gam đường cần dùng là .
b)Biểu thức biểu diễn số gam hương liệu cần dùng là .
c) Cặp thỏa mãn bài toán thuộc miền nghiệm của hệ.
d) Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Để đạt điểm
thưởng lớn nhất thì cần pha chế lít nước cam và lít nước táo.
Lời giải
a) Để pha chế 1 lít nước cam cần 30g đường và để pha chế 1 lít nước táo cần 10g đường nên biểu thức biểu
diễn số gam đường cần dùng là
b) Để pha chế 1 lít nước cam cần 1g hương liệu và để pha chế 1 lít nước táo cần 4g hương liệu nên biểu thức
số gam hương liệu cần dùng là
c) Để pha chế 1 lít nước cam cần 30g đường và để pha chế 1 lít nước táo cần 10g đường nên biểu thức biểu
diễn số gam đường cần dùng là và mỗi đội chơi được sử dụng 210g đường để pha chế nước cam và nước táo
nên ta có bất phương trình
Để pha chế 1 lít nước cam cần 1g hương liệu và để pha chế 1 lít nước táo cần 4g hương liệu nên biểu thức số
gam hương liệu cần dùng là và mỗi đội chơi được sử dụng tối đa 24g hương liệu để pha chế nước cam và
nước táo nên ta có bất phương trình
Để pha chế 1 lít nước cam cần 1 lít nước và để pha chế 1 lít nước táo cần 1 lít nước nên biểu thức số lít nước
cần dùng là và mỗi đội chơi được sử dụng tối đa 9 lít nước để pha chế nước cam và nước táo nên ta có bất
phương trình
Điều kiện
d) Số điểm thưởng nhận được khi pha lít nước cam và lít nước táo là
Dựa vào hình biểu diễn của hệ bất phương trình ta có số điểm thưởng lớn nhất là
Dạng thức 3
Câu 1.Tìm tất cả các giá trị của tham số để với mọi cặp số thoả mãn hệ bất phương trình sau:
Lời giải
Miền nghiệm của hệ bất phương trình là miền tứ giác với , Hinh). Ta có: .
Đặt . Tính giá trị của tại các cặp số là toạ độ của các đỉnh tứ giác rồi so sánh bằng tại .
Để với mọi thoả mãn hệ bất phương trình đã cho thì trên miền nghiệm của hệ bất phương trình đó hay .
Câu 2. Một trận bóng đá được tổ chức tại một sân vận động có sức chứa 40 000 người, ban tổ chức phát hành
hai loại vé là 400 000 đồng và 200 000 đồng. Do điều kiện sân đấu nên số lượng vé có giá 400 000 đồng
không lớn hơn số lượng vé có giá 200 000 đồng. Để an toàn phòng dịch, liên đoàn bóng đá yêu cầu số lượng
vé phát hành không được quá 30% sức chứa của sân. Tìm số tiền lớn nhất thu được qua bán vé.
Lời giải
Gọi lần lượt là số vé giá 400 000 đồng và 200 000 đồng được bán ra
Do điều kiện sân đấu nên số lượng vé có giá 400 000 đồng không lớn hơn số lượng vé có giá 200 000 đồng
nên ta có bất phương trình
Một trận bóng đá được tổ chức tại một sân vận động có sức chứa 40 000 người và để an toàn phòng dịch, liên
đoàn bóng đá yêu cầu số lượng vé phát hành không được quá 30% sức chứa của sân nên ta có bất phương
trình
Ta có hệ bất phương trình sau:
Tổng số tiền thu được qua bán vé là
Suy ra số tiền lớn nhất là 3600000000 đồng.
Câu 3.Bạn Lan có 150000 đồng, Lan muốn mua một số quyển tập và bút. Biết rằng giá một quyển tập là
8000 đồng và giá của một cây bút là 6000 đồng. Bạn Lan đã mua 10 cây bút, hỏi Lan có thể mua tối đa bao
nhiêu quyển tập.
Lời giải
Gọi lần lượt là số quyển tập và số cây bút
Bất phương trình biểu diễn số tập và bút có thể mua được phụ thuộc vào số tiền mang theo là
Bạn Lan đã mua 10 cây bút nên ta có
Vì nguyên dương nên số quyển tập tối đa bạn Lan mua được là 11 quyển.
Câu 4. Tìm các giá trị của tham số sao cho là nghiệm của bất phương trình
Lời giải
Ta có là nghiệm của bất phương trình khi và chỉ khi
Trả lời:
Câu 5. Một hộ nông dân định trồng bắp và khoai lang trên diện tích . Trên diện tích mỗi , nếu trồng bắp thì
cần công và thu lợi nhuận triệu đồng, nếu trồng khoai lang thì cần 15 công và thu lợi nhuận 2,5 triệu đồng.
Biết rằng tổng số công không quá 45 công. Gọi (ha) là diện tích trồng bắp và (ha) là diện tích trồng khoai
lang để thu được lợi nhuận lớn nhất. Tính ?
Lời giải
Gọi lần lượt là số trồng bắp và khoai lang.
Điều kiện ;
Số tiền thu được là (triệu đồng).
Ta có hệ
Bài toán trở thành tìm giá trị lớn nhất của trên miền nghiệm của hệ .
Tìm tọa độ các điểm .
Tọa độ điểm là nghiệm của hệ . Vậy .
Tọa độ điểm là nghiệm của hệ . Vậy .
Tọa độ điểm là nghiệm của hệ . Vậy .
Tọa độ điểm .
Ta thấy đạt giá trị lớn nhất chỉ có thể tại các điểm .
Tại thì (triệu đồng).
Tại thì (triệu đồng).
Tại thì (triệu đồng).
Tại thì (triệu đồng).
Vậy cần trồng bắp và khoai lang để thu được số tiền nhiều nhất.
Trả lời: 7
Câu 6. Một phòng học có chiều dài và chiều rộng Diện tích để kê một chiếc ghế là một chiếc bàn là Gọi là
số chiếc ghế, là số bàn được kê. Biết diện tích mặt sàn dành cho lưu thông tối thiểu là Hỏi trong phòng học
kê được tối đa bao nhiêu bộ bàn ghế?
Lời giải
Diện tích số ghế là
Diện tích số bàn là
Tổng số diện tích số ghế và số bàn là
Diện tích phòng học là
Diện tích tối đa để kê các bộ bàn ghế là