T r a n g 1 | 18
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT LINH TRUNG
TỔ TOÁN
ĐỀ CHÍNH THỨC
ĐỀ
THI THỬ
LẦN
1
NĂM HỌC 2021
–
2022
MÔN: TOÁN – KHỐI 12
THỜI GIAN: 90 phút (trắc nghiệm)
(không kể thời gian giao đề)
Câu 1: Cho cấp số nhân
( )
n
u
có
12
3; 9uu= − =
. Giá trị của
3
u
là bao nhiêu?
A.
21
. B.
9−
. C.
12
. D.
27−
.
Câu 2: Một hình nón có diện tích đáy bằng
(đvdt) có chiều cao
3h=
. Thể tích khối
nón tương ứng bằng
A.
16
(đvtt). B.
16
3
(đvtt). C.
16
3
(đvtt). D.
8
(đvtt).
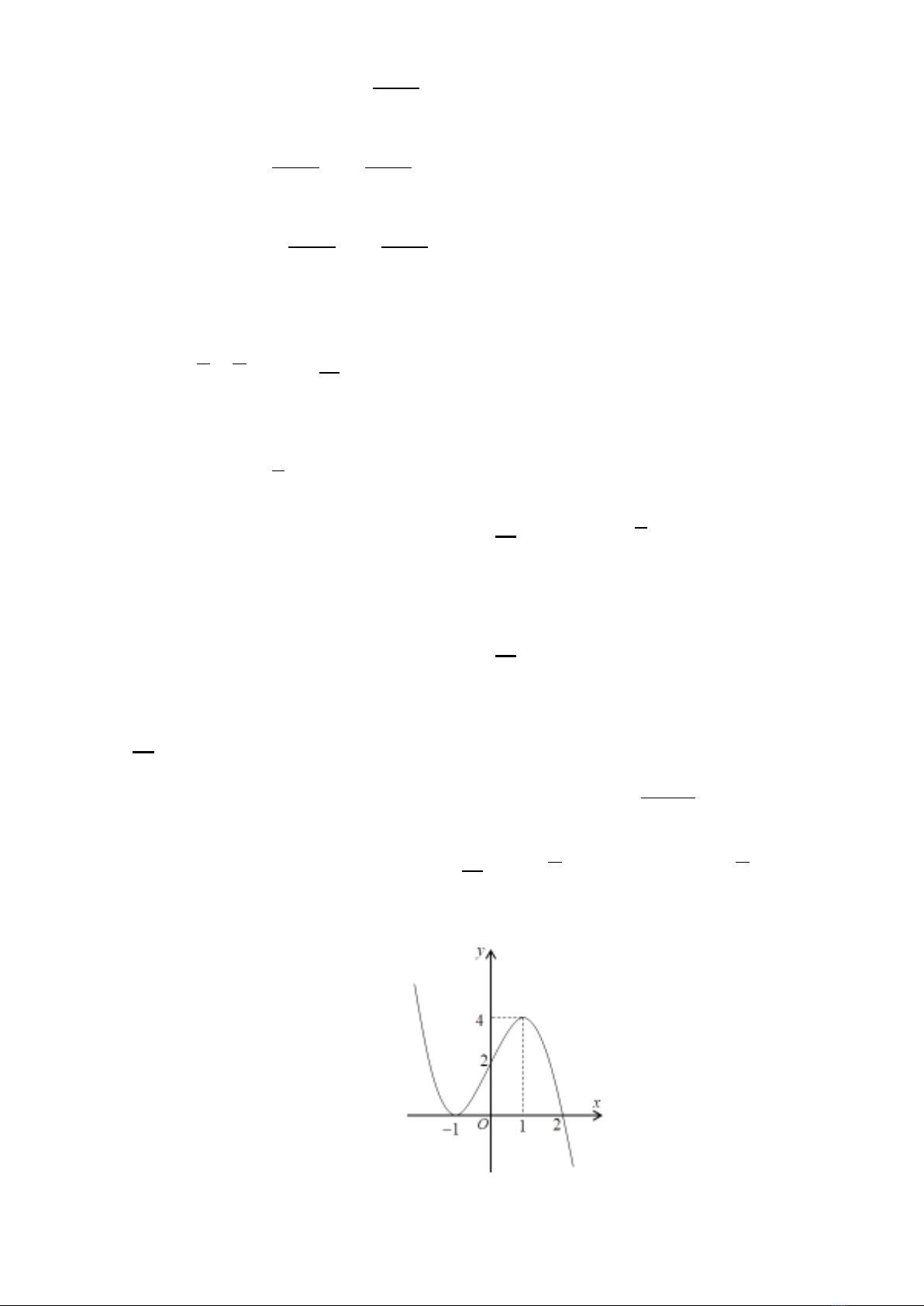
Câu 3: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây:
A.
( )
1;3
. B.
( )
;1−
. C.
( )
0;2
. D.
( )
0;+
.
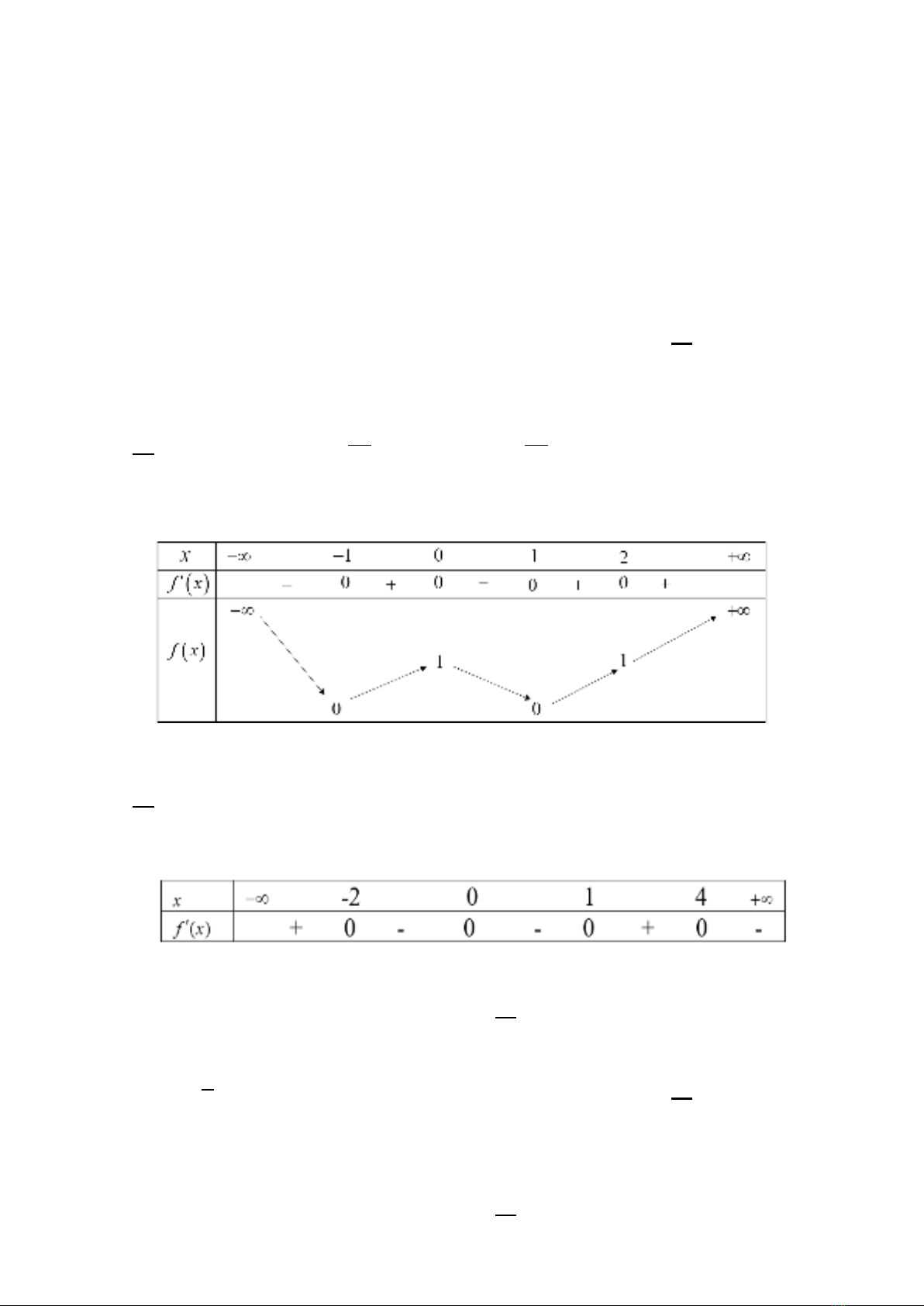
Câu 4: Cho hàm số
()fx
có bảng xét dấu đạo hàm
()fx
như sau
Hàm số
()fx
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
D.
4
.
Câu 5: Công thức tính thể tích
V
của khối trụ có bán kính đáy
r
và chiều cao
h
là
A.
2
1
3
V r h
=
. B.
V rh
=
. C.
2V rh
=
. D.
2
V r h
=
.
Câu 6: Lớp 12A có 40 học sinh, trong đó có 25 học sinh nam và 15 học sinh nữ. Hỏi có bao
nhiêu cách chọn ra một nhóm gồm 5 học sinh nữ đi tập văn nghệ?
A.
5
40
C
. B.
5
40
A
. C.
5
15
C
. D.
5
25
C
.
T r a n g 2 | 18
Câu 7: Tích phân
ln2021
ln2020
x
e dx
bằng
A.
4.
B.
e
C.
ln 2021 ln 2020.−
D.
1.
Câu 8: Nếu
( )
2
0
d5f x x =
và
( )
2
0
d3g x x =−
thì
( ) ( )
2
0
3df x g x x−


bằng
A.
14
. B.
. C.
8
. D.
2
.
Câu 9: Một hình nón có bán kính đáy
4r=
cm và độ dài đường sinh
5l=
cm . Diện tích
xung quanh của hình nón đó bằng
A.
2
20 cm
. B.
2
40 cm
. C.
2
80 cm
. D.
2
10 cm
.
Câu 10: Cho số phức
34zi=−
. Số phức
42w z i= − +
bằng
A.
12wi= − −
. B.
76wi=−
. C.
12wi= − +
. D.
16wi= − −
.
Câu 11: Phương trình
21
5 125
x−=
có nghiệm là
A.
2.x=
B.
1.x=
C.
3.x=
D.
6.x=
Câu 12: Cho số phức
43zi=−
. Môđun của số phức
.zi
bằng
A.
5
. B.
25
. C.
7
. D.
1
.
Câu 13: Trong mặt phẳng phức (hình dưới), số phức
43zi= − +
được biểu diễn bởi
A. Điểm
A
. B. Điểm
B
. C. Điểm
C
. D. Điểm
D
.
Câu 14: Cho số phức
( )( )
6 4 2
1
ii
zi
−+
=+
. Số phức
.w z i z=−
có phần thực bằng.
A.
2
. B.
2−
. C.
16
. D.
16−
.
Câu 15: Cho hàm số
( )
1
cos 2020 .
2021
f x x

=+


Trong các khẳng định sau, khẳng định
nào đúng?
A.
( )
1
2021sin 2020 .
2021
f x dx x C

= + +


x
y
4
4
3
3
B
C
D
4
3
A
O
T r a n g 3 | 18
B.
( )
1
2021sin 2020 .
2021
f x dx x C

= − + +


C.
( )
11
sin 2020 .
2021 2021
f x dx x C

= + +


D.
( )
11
sin 2020 .
2021 2021
f x dx x C

= − + +


Câu 16: Cho số phức
z
thỏa mãn
( )
1 2 1 3z i i+ = − +
khẳng định nào sau đây đúng?
A.
11
22
zi
=−
B.
1zi=+
C.
zi=
D.
2zi=−
Câu 17: Cho hàm số
( )
32
x
f x e=−
. Trong các khẳng định sau, khẳng định nào đúng.
A.
( )
1
d2
3
x
f x x e x C= − +
. B.
( )
3
d2
x
f x x e x C= − +
.
C.
( )
3
d 3 2
x
f x x e x C= − +
. D.
( )
3
1
d2
3
x
f x x e x C
= − +
.
Câu 18: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
3;0;0M
,
( )
0;0;4N
. Tính
độ dài đoạn thẳng
MN
.
A.
1MN =
. B.
7MN =
C.
5MN =
. D.
10MN =
Câu 19: Đồ thị hàm số
( )
( )
22021 3y x x= + −
cắt trục hoành tại mấy điểm ?
A. 1. B. 2. C. 3. D. 4.
Câu 20: Phương trình đường tiệm cận đứng của đồ thị hàm số
1
21
x
yx
+
=+
là
A.
2x=
. B.
2x=−
. C.
1
2
x=−
. D.
1
2
x=
.
Câu 21: Cho hàm số có đồ thị như hình vẽ:
Hàm số nào dưới đây có đồ thị là hình vẽ trên?
T r a n g 4 | 18
A.
42
42y x x= − +
.
B.
332y x x= − +
.
C.
42
42y x x= − + +
.
D.
332y x x= − + +
.
Câu 22: Với
a
,
b
là hai số thực dương tuỳ ý,
( )
2
log ab
bằng
A.
( )
2 log logab+
. B.
1
log log
2
ab
+
. C.
2log logab+
. D.
log 2logab+
.
Câu 23: Mặt cầu có diện tích bằng
64
thì có bán kính bằng
A.
4
. B.
8
. C.
8
. D.
4
.
Câu 24: Giá trị nhỏ nhất của hàm số
321y x x=−
trên
0;10
bằng
A.
34−
. B.
14 7−
. C.
0
. D.
33−
.
Câu 25: Tập nghiệm của bất phương trình
2
33
log 6log 8 0xx− +
là
[ ; ]ab
. Tính
ab+
.
A.
90
. B.
729
. C.
8
. D.
6
.
Câu 26: Với
a
là số thực dương tùy ý,
2
3a
bằng
A.
6
a
. B.
1
6
a
. C.
3
2
a
. D.
2
3
a
.
Câu 27: Trong không gian
Oxyz
, cho
( )
1;3;2u
. Đường thẳng nào sau đây nhận véc tơ
u
làm
véc tơ chỉ phương:
A.
1
12
:3
2
xt
yt
zt
=+
= +
=−
. B.
2:3
2
xt
yt
zt
=
= −
=
.
C.
2
2
: 1 3
22
xt
yt
zt
=+
= +
= − +
. D.
4
2
: 1 3
22
xt
yt
zt
=−
= +
= − +
.
Câu 28: Trong không gian
Oxyz
, mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 1 2 11S x y z− + + + − =
có tọa độ tâm là
A.
( )
1;1;2 .
B.
( )
1; 1;2 .−
C.
( )
2; 2;4 .−
D.
( )
1;1; 2 .−−
Câu 29: Đạo hàm của hàm số
5
logyx=
là :
A.
ln5
yx
=
. B.
ln5
x
y=
. C.
1
.ln5
yx
=
. D.
' .ln5yx=
.
Câu 30: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như sau:
T r a n g 5 | 18
Hàm số có bao nhiêu điểm cực đại ?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 31: Nghiệm của bất phương trình
42
22
33
xx−
là:
A.
2
3
x−
. B.
2
3
x
. C.
2
5
x
D.
2
5
x
Câu 32: Trong không gian với hệ trục tọa độ
,Oxyz
cho điểm
( )
2; 1;3M−
. Khi đó tọa độ
hình chiếu vuông góc
'M
của
M
trên mặt phẳng
Ox
là
A.
( )
' 0;0;3 .M
B.
( )
' 0; 1;0 .M−
C.
( )
' 4;0;0 .M
D.
( )
' 2;0;0 .M
Câu 33: Trong không gian với hệ toạ độ
Oxyz
, cho
( )
1;0;0A
,
( )
0;2;0B
,
( )
0;0;3C
. Khi đó
phương trình mặt phẳng
( )
ABC
là:
A.
1
1 2 3
x y z
+ + =
. B.
1
2 1 3
x y z
+ + =
. C.
1
1 3 2
x y z
+ + =
. D.
1
3 2 1
x y z
+ + =
.
Câu 34: Trong không gian
Oxyz
cho điểm
(1; 1;2), (3;0;1)AB−
. Đường thẳng vuông góc
với
AB
tại A đồng thời song song với mặt phẳng
( ): 2 0P x y z+ + =
có phương
trình là:
A.
1
1
2
xt
yt
zt
=+
= − +
=+
. B.
1
1
2
xt
yt
zt
=+
= − −
=+
. C.
3
1
xt
yt
zt
=+
=−
=+
. D.
13
1
23
xt
yt
zt
=+
= − −
=+
.
Câu 35: Trong không gian với hệ tọa độ
Oxyz
, mặt cầu
()S
tâm
( )
1;2; 3I−
và đi qua điểm
( )
1;0;4A
có phương trình là
A.
( ) ( ) ( )
2 2 2
1 2 3 53x y z− + − + + =
. B.
( ) ( ) ( )
2 2 2
1 2 3 53x y z+ + + + − =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 53x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 53x y z+ + + + + =
.
Câu 36: Cho hình lăng trụ đứng
.ABC A B C
(minh họa như hình vẽ bên). Biết tam giác
ABC
đều cạnh bằng
a
, cho
3
2
a
AA=
. Gọi
I
là trung điểm của
AB

. Tính góc
giữa đường thẳng
CI
và mặt phẳng
( )
ABC
.