S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ K THI TUY N SINH L P 10 THPTỲ Ể Ớ
T NH PHÚ YÊNỈNĂM H C 2021 – 2022Ọ
Đ CHÍNH TH CỀ Ứ Môn thi: TOÁN
(Đ thi có 2 trang)ềTh i gian làm bài: 120 phút, không k th i gian phát đ)ờ ể ờ ề
I. TR C NGHI M Ắ Ệ (3,00 đi m)ể
H c sinh ch n m t ph ng án đúng nh t m i câu và vi t ph ng án ch n vào bài làmọ ọ ộ ươ ấ ở ỗ ế ươ ọ
(Ví d : Câu 1: A, Câu 2: B, Câu 3: D,…)ụ
Câu 1. Tr c căn th c m u c a bi u th c ta đc k t qu làụ ứ ở ẫ ủ ể ứ ượ ế ả
A. A. .B. .C. .D. .
B. Câu 2. Đng th c nào sau đây đúng?ẳ ứ
C. A. .B. .C. .D. .
D. Câu 3. Đng th ng đi qua đi m có h s góc b ngườ ẳ ể ệ ố ằ
E. A. .B. .C. .D. .
F. Câu 4. Tìm và bi t h ph ng trình có nghi m duy nh t là .ế ệ ươ ệ ấ
G. A. ; . B. ; . C. ; . D. ; .
H. Câu 5. Tìm t t c các giá tr c a tham s đ ph ng trình có nghi m.ấ ả ị ủ ố ể ươ ệ
I. A. . B. .C. .D. .
J. Câu 6. Đi m nào sau đây ểkhông thu c đ th hàm s ?ộ ồ ị ố
K. A. .B. .C. .D. .
L.
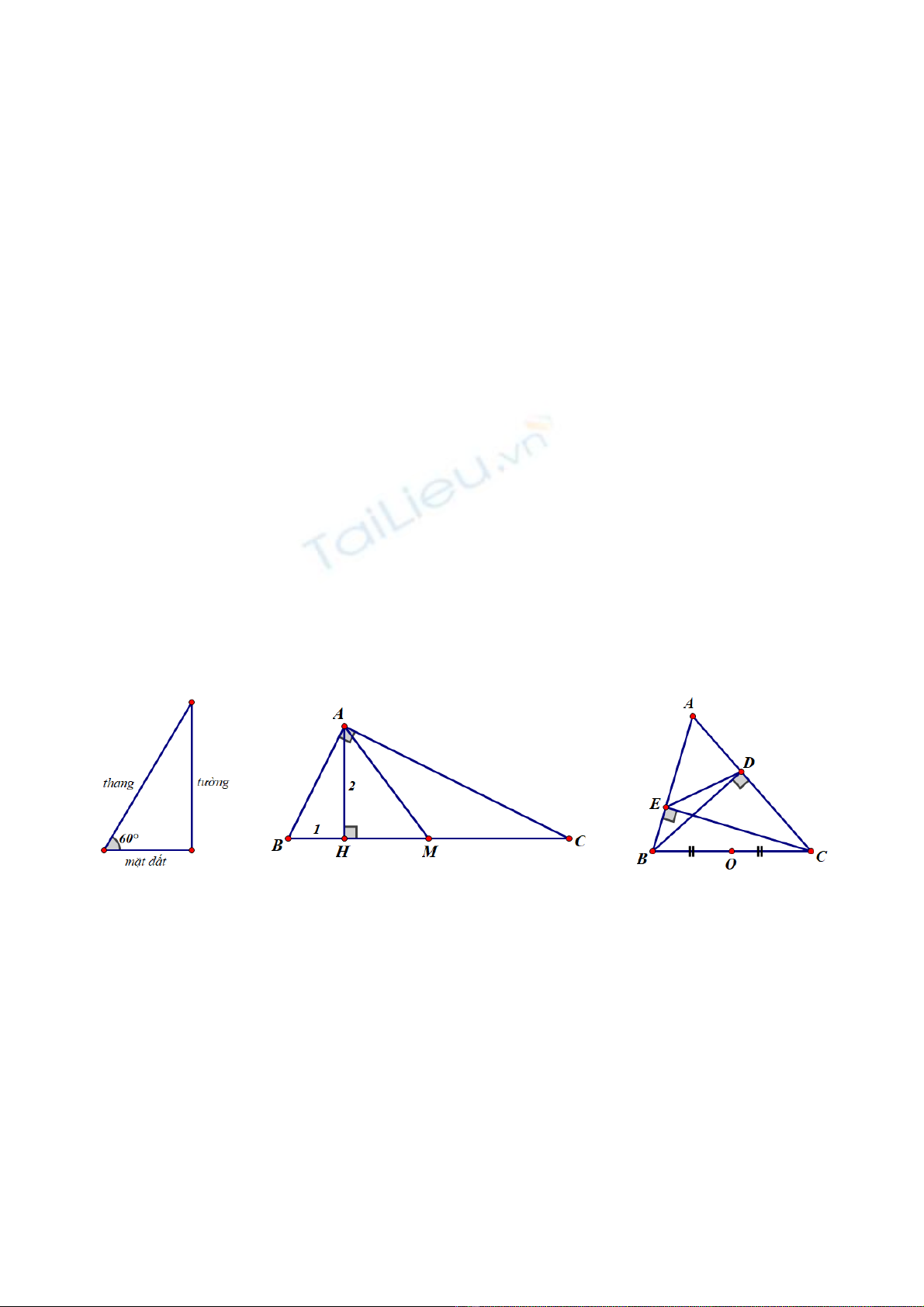
M. Hình 1
N.
O. Hình 2
P.
Q. Hình 3
R. Câu 7. M t cái thang dài , đt t o m t đt m t góc b ng (Hình 1). V y chân thang cáchộ ặ ạ ặ ấ ộ ằ ậ
t ng bao nhiêu mét?ườ
S. A. .B. .C. .D. .
T. Câu 8. Cho tam giác vuông t i , có đng cao , trung tuy n . Bi t , (Hình 2). Kh ngạ ườ ế ế ẳ
đnh nào sau đây ịsai?
U. A. .B. .C. .D. .
V. Câu 9. Cho tam giác nh n , có các đng cao , ; là trung đi m c a (Hình 3). Kh ngọ ườ ể ủ ẳ
đnh nào sau đây ịsai?
W. A. .B. .C. D. .
X.
Y. Hình 4
Z.
AA. Hình 5
AB.
AC. Hình 6
AD. Câu 10. Cho đng tròn tâm bán kính b ng , cung b ng đ. Ti p tuy n t i c tườ ằ ằ ộ ế ế ạ ắ
t i (Hình 4). Tính đ dài đo n .ạ ộ ạ
AE. A. .B. .C. .D. .
AF. Câu 11. Cho đng tròn tâm đng kính ; là đi m ngoài đng tròn. G i ,ườ ườ ể ở ườ ọ
l n l t là giao đi m c a , v i đng tròn (Hình 5). Tính , bi t .ầ ượ ể ủ ớ ườ ế
AG. A. .B. .C. .D. .
AH. Câu 12. Cho hai đng tròn và ti p xúc nhau (Hình 6). Tính di n tích mi n tôườ ế ệ ề
đm t o b i đng tròn và đng tròn .ạ ạ ở ườ ườ
AI. A. .B. .C. .D. .
II. T LU N Ự Ậ (7,00 đi m)ể
AJ.Câu 13. (1,50 đi m)ể Gi i các ph ng trình sau:ả ươ
a) ; b) ; c) ;
d) Câu 14. (1,50 đi m)ể Cho hàm s .ố
a) Xác đnh h s bi t r ng đ th c a hàm s c t đng th ng t i đi m có hoành đị ệ ố ế ằ ồ ị ủ ố ắ ườ ẳ ạ ể ộ
b ng .ằ
b) V đ th c a hàm s và đ th hàm s v i giá tr c a v a tìm đc câu a) trên cùngẽ ồ ị ủ ố ồ ị ố ớ ị ủ ừ ượ ở
m t m t ph ng t a đ.ộ ặ ẳ ọ ộ
c) D a vào đ th , hãy xác đnh t a đ giao đi m th hai (khác ) c a hai đ th v a v trongự ồ ị ị ọ ộ ể ứ ủ ồ ị ừ ẽ
câu b).
e) Câu 15. (2,00 đi m)ể Gi i bài toán b ng cách l p ph ng trình ho c h ph ng trìnhả ằ ậ ươ ặ ệ ươ
f) Quãng đng g m m t đo n lên d c dài và m t đo n xu ng d c dài . M t ng i đi xeườ ồ ộ ạ ố ộ ạ ố ố ộ ườ
đp t đn h t gi phút và đi t v h t gi phút (v n t c lên d c, xu ng d c lúcạ ừ ế ế ờ ừ ề ế ờ ậ ố ố ố ố
đi và v nh nhau). Tính v n t c lúc lên d c, lúc xu ng d c c a ng i đi xe đp.ề ư ậ ố ố ố ố ủ ườ ạ
g) Câu 16 (2,00 đi m)ể Cho hình thang có , , . G i là trung đi m c a , ọ ể ủ là hình chi u vuôngế
góc c a lên . Tia c t đng th ng t i .ủ ắ ườ ẳ ạ
a) Ch ng minh r ng .ứ ằ
b) Ch ng minh r ng là hình bình hành.ứ ằ
c) Đng thườ ngẳ qua vuông góc v i c t c nh t i . G i là hình chi u vuông góc c a lên . ớ ắ ạ ạ ọ ế ủ
Ch ng minh r ng tam giác cân.ứ ằ
d) Ch ng minh r ng đng th ng đi qua trung đi m c a .ứ ằ ườ ẳ ể ủ
h)
____________________ H T ____________________Ế
I. TR C NGHI MẮ Ệ
i) Câ
u
j)
1
k
)
2
l)
3
m
)
4
n
)
5
o
)
6
p
)
7
q
)
8
r
)
9
s
)
1
t)
1
u
)
1
v) Đá
p
án
w
)
A
x
)
C
y
)
B
z
)
D
a
a
)
A
a
b
)
B
a
c
)
A
a
d
)
B
a
e
)
D
a
f
)
D
a
g
)
C
a
h
)
C
ai) Câu 1. Ta có: . Ch n Aọ
aj) Câu 2. Khai ph ng m t tích, ta có: ươ ộ Ch n Cọ
ak)Câu 3. Ta th vào , ta đc: ế ượ Ch n Bọ
al) Câu 4. Th vào HPT, ta đc: ế ượ
am)
Ch n Dọ
an)Câu 5. PT có nghi m ệCh n Aọ
ao)Câu 6. Ta th vào , ta đc: (Vô lý)ế ượ Ch n Bọ
ap)Câu 7. Ta có: Ch n Aọ
aq)Câu 8. Áp d ng đnh lý Pytago cho vuông t i , ta có:ụ ị ạ
ar)
Ch n Bọ
as) Câu 9. Xét t giác , ta có: (gt)ứ
at) vuông t i và vuông t i cùng nhìn d i m t góc vuông ạ ạ ướ ộ
au) T giác n i ti p đng tròn nh n là đng kínhứ ộ ế ườ ậ ườ
av) Mà là trung đi m (gt) ể (A đúng)
aw) Ta có: (T giác n i ti p đng tròn nh n là đng kính) (B đúng)ứ ộ ế ườ ậ ườ
ax) Xét có: (b t đng th c tam giác) (C đúng)ấ ẳ ứ
Ch n Dọ
ay)Câu 10. Xét vuông t i có: ạCh n Dọ
az) Câu 11. Ta có: n i ti p đng tròn nh n đng kínhộ ế ườ ậ ườ
ba) Xét vuông t i có: ạ
Ch n C ọ
bb)Câu 12. Ta có: Ch n Cọ
II. T LU NỰ Ậ
bc)Câu 13. (1,50 đi m)ể Gi i các ph ng trình sau:ả ươ
a) ; b) ; c) ;
d) L i gi iờ ả
a)
e) V y là nghi m c a ph ng trình.ậ ệ ủ ươ
b) Gi i ph ng trình: (; ; )ả ươ
f) Ta có: nên ph ng trình luôn có hai nghi mươ ệ
g) và
h) V y ph ng trình có t p nghi m ậ ươ ậ ệ
c) Gi i ph ng trình: ả ươ
i) Đt v i . Khi đó ph ng trình tr thànhặ ớ ươ ở
j) (th a mãn đi u ki n)ỏ ề ệ
k) V i thì ớ
l) V y ph ng trình đã cho có t p nghi m ậ ươ ậ ệ
m) Câu 14. (1,50 đi m)ể Cho hàm s .ố
a) Xác đnh h s bi t r ng đ th c a hàm s c t đng th ng t i đi m có hoành đị ệ ố ế ằ ồ ị ủ ố ắ ườ ẳ ạ ể ộ
b ng .ằ
b) V đ th c a hàm s và đ th hàm s v i giá tr c a v a tìm đc câu a) trên cùngẽ ồ ị ủ ố ồ ị ố ớ ị ủ ừ ượ ở
m t m t ph ng t a đ.ộ ặ ẳ ọ ộ
c) D a vào đ th , hãy xác đnh t a đ giao đi m th hai (khác ) c a hai đ th v a v trongự ồ ị ị ọ ộ ể ứ ủ ồ ị ừ ẽ
câu b).
n) L i gi iờ ả
a) Xét ph ng trình hoành đ giao đi m: (1)ươ ộ ể
o) Do đ th hàm s c t đng th ng t i đi m có hoành đ b ng nên ta có là m tồ ị ố ắ ườ ẳ ạ ể ộ ằ ộ
nghi m c a ph ng trình (1).ệ ủ ươ
p) Thay vào ph ng trình (1), ta có: .ươ
q) V y .ậ
b) V đ th hàm s ẽ ồ ị ố
r) Ta có b ng giá tr :ả ị
s) t) u)
v) w) x)
y) Do đó, đ th hàm s là đng th ng đi qua hai đi m và ồ ị ố ườ ẳ ể
z) V đ th hàm s ẽ ồ ị ố
aa) Đ th hàm s b c hai và có h s nên đ th có d ng Parabol và có b lõm h ng lênồ ị ố ậ ệ ố ồ ị ạ ề ướ
trên. Hàm s đng bi n khi và ngh ch bi n khi ố ồ ế ị ế
ab) Ta có b ng giá tr :ả ị
ac)
ad) ae)
af) ag)
ah)
ai)
aj) ak)
al) am)
an)
ao) Do đó, đ th hàm s là đng cong đi qua các đi m , , , và ồ ị ố ườ ể
ap) V đ th hàm sẽ ồ ị ố