
Kü thuËt §å ho¹ m¸y tÝnh
58
Pv PG v
iijj
j
m
() ()=
=
∑
0
⇒ MÆt cong s cã thÓ viÕt d−íi d¹ng
Suv PF uG v
ij i j
j
m
i
n
(,) () () ()=
== ∑∑ 2
00
Víi Fi(u), Gj(v) lµ c¸c hµm c¬ së
NÕu chän hµm c¬ së
Fu l u uu
uu
ii
ni
ki
k
ki
n
() ()== −
−
=
≠
∏
0
Gv l v
v
v
vv
jj
mj
kj
k
kj
m
() ()==
−
−
=
≠
∏
0
khi ®ã
Suv Pl vl u
ij j
mi
n
j
m
i
n
(,) () () (**)=
== ∑∑ 00
Chóng ta thÓ thÊy mÆt cong s ®i qua ®iÓm Ui,vj
S(ui,vj)=Pij
C«ng thøc (**) gäi lµ c«ng thøc mÆt cong Lagrang
MÆt cong Lagrang cã −u ®iÓm nã ®i qua nxm ®iÓm cho tr−íc vµ cã ®¹o hµm cao tuú
ý. Do vËy nãi chung mÆt cong Lagrang cã sai sè rÊt lín so víi mÆt cong thùc ph¶i
x©y dùng
$11. MÆt cong Bezier
1. MÆt cong Bezier
T×nh h×nh gièng nh− víi ®−êng cong ®Ó cã thÓ x©y dùng mÆt cong chÝnh x¸c h¬n khi
cho tr−íc mét sè ®iÓm, ng−êi ta nghÜ ®Õn viÖc x©y dùng c¸c m¶nh mÆt cong nhá h¬n
vµ sau ®ã ghÐp nèi chóng l¹i, mÆt cong Bezier lµ mÆt cong cã d¹ng tham sè:
Suv PB uB v
ij m
jn
i
j
m
i
n
(,) () () ()=== ∑∑ 2
00
ë ®©y BB
m
jn
i
, lµ c¸c ®a thøc Berstein bËc m vµ n, uo≤u≤u1 , vo≤v≤v1
Kü thuËt §å ho¹ m¸y tÝnh
59
u=uo+q(u1-uo) v=vo+r(v1-vo)
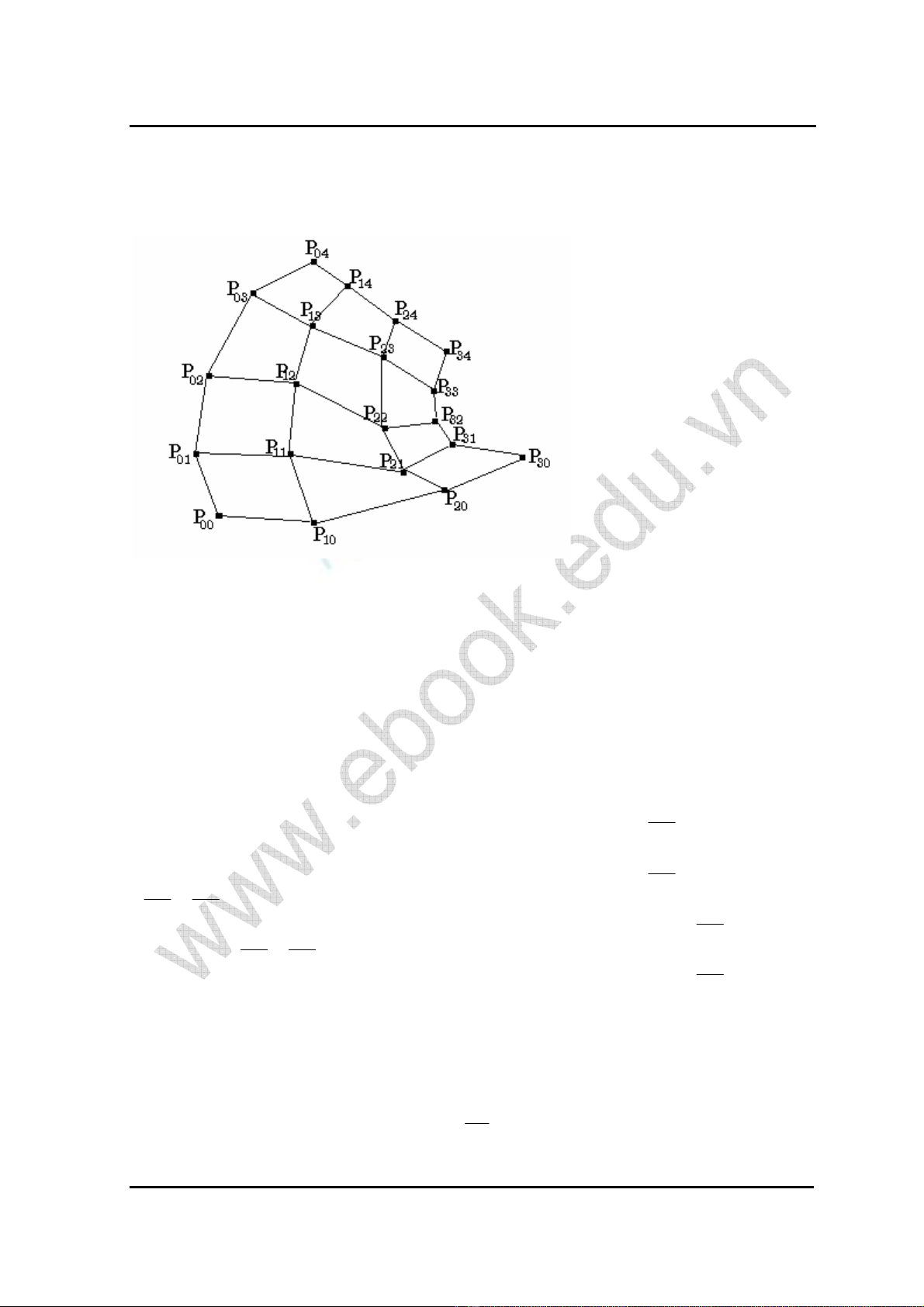
C¸c ®iÓm Pij ®−îc gäi lµ c¸c ®iÓm kiÓm tra cña mÆt cong Bezier. Cã thÓ minh ho¹
c¸c ®iÓm nµy s¾p xÕp theo trËt tù sau
Suy tõ c¸ch x©y dùng ®−êng cong Bezier, chóng ta cã thÓ nhËn thÊy 4 ®iÓm
Poo,Pom,Pno,Pnm lµ nh÷ng ®iÓm ch¾c ch¾n thuéc mÆt cong S. XÐt tr−êng hîp
n=m=3 khi ®ã mèi liªn hÖ vÒ gi¸ trÞ vµ ®¹o hµm riªng ë c¸c nót Poo,Pom,Pno,Pnm
®−îc cho bëi c«ng thøc sau:
Su v Su v S u v S u v
Su v Su v S u v S u v
SuvSuvSuvSuv
SuvSuvSuvSuv
vv
vv
u u uv uv
uuu
v
u
v
(,) (,) (,) (,)
(,) (,) (,) (,)
(,) (,) (,) (,)
(,) (,) (,) (,)
''
''
''' '
''' '
00 01 00 01
10 11 10 11
00 01 00 01
10 11 10 11
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
1000
0001
33 00
00 33
10 30
00 30
00 0 3
00 1 3
00 01 02 03
10 11 12 13
20 21 22 23
30 31 32 33
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
ΔΔ
ΔΔ
Δ
Δ
Δ
Δ
uu
uu
PPPP
PPPP
PPPP
PPPP
v
v
v
v
Δu=u1-u0; Δv=v1-v0;
VÝ dô: Tõ mèi liªn hÖ trªn ta cã:
S(u1,v1)=P33
Su(u1,v1)= 3
Δ
u (P33-P23)

Kü thuËt §å ho¹ m¸y tÝnh
60
Sv(u1,v1)= 3
Δ
v
(P33-P32)
Suv(u1,v1)=
9
Δ
Δ
u
v
(P22-P32-P23+P33)
2. D¸n c¸c mÆt cong Bezier
Gi¶ sö chóng ta ®· x©y dùng ®−îc 2 mÆt cong Bezier S1(u,v) nµ S2(u,v)
S1(u,v) ë ®©y cã miÒn x¸c ®Þnh [uo,u1]x[vo,v1]
S2(u,v) cã miÒn x¸c ®Þnh [u1,u2]x[vo,v1]
Gi¶ sö ta cÇn ph¶i d¸n S1 vµ S2 däc theo biªn u=u1 khi ®ã:
Víi hµm S1 ta ®Æt:
u=uo+p(u1-uo)
v=vo+r(v1-vo)
⇒=
== ∑∑
Suv PBpB r
ij n
im
j
j
m
i
n
11
00
(,) () () (*)
,
Víi hµm S2 ta ®Æt
u=u1+q(u2-u1)
v=vo+r(r1-ro)
⇒=
== ∑∑
Suv PBqB r
ij n
im
j
j
m
i
n
22
00
(,) () () (**)
,
Chóng ta cã nhËn xÐt trªn biªn u=u1 c¸c ®iÓm kiÓm tra cña ®−êng cong Bezier t¹o
nªn biªn u=u1 ®iÓm cuèi cña ®−êng Bezier theo v trªn S1 lµ ®iÓm ®Çu cña ®−êng
cong Bezier trªn u2
⇒= ∀=PP jm
nj j
10
20, (***)
§iÒu kiÖn hai ®iÓm cho c¸c ®−êng Bezier theo v nèi víi nhau vµ liªn tôc trªn bê u.
ViÖc nèi ®Ó b¶o ®¶m tÝnh tr¬n cña mÆt cong ®−a vÒ bµi to¸n nèi c¸c ®−êng cong
Bezier
Bezier theo tham sè v tr¬n ë c¸c ®iÓm
vo
v1
S2
S1
u2
u1
uo

Kü thuËt §å ho¹ m¸y tÝnh
61
⇒== =PPP jm
nj j j
10
20, .
Ch−¬ng tr×nh minh häa :
USES graph,crt;
Const l=3;
VAR
pi:array[0..l] of real;
u,v,t: real;
xi,yi,zi,a,b,c:array[0..l,0..l] of real;
x,y,z:array[0..100] of real;
xdau,Gd,Gm,i,j,k,p:integer;
a1,b1,s:real;
st1,st2: string[1];
(*************************************************)
{-------------Ve he truc toa do------------}
procedure khoitao;
begin
Gd := Detect;
InitGraph(Gd, Gm, ' ');
if GraphResult <> grOk then Halt(1);
directvideo:=False;
setbkcolor(1);
setcolor(14);
setviewport(getmaxX div 2,getmaxY div 2,getmaxX,getmaxY,false);
setlinestyle(0,0,0);
line(0,0,320,0);
line(-0,0,0,-240);
line(0,0,-240,240);
line(-5,-230,0,-240);
line(5,-230,0,-240);
line(310,-5,320,0);
line(310,5,320,0);
line(228,-235,240,-240);
line(235,-228,240,-240);
setlinestyle(1,0,0);
line(-320,0,0,0);
line(0,0,240,-240);
line(0,0,0,240);
settextjustify(0,2);
outtextxy(5,5,'O');
outtextxy(305,10,'x');
outtextxy(10,-230,'y');
outtextxy(240,-230,'z');
setlinestyle(0,0,0);
end;

Kü thuËt §å ho¹ m¸y tÝnh
62
(*************************************************)
procedure move_to(x,y,z: integer);
Begin
moveto(round(x+z/sqrt(2)),round(y+z/sqrt(2)));
End;
(*************************************************)
procedure line_to(x,y,z: integer);
Begin
lineto(round(x+z/sqrt(2)),round(y+z/sqrt(2)));
End;
(*************************************************)
procedure put_pixel(x,y,z,m : integer);
Begin
putpixel(round(x+z/sqrt(2)),round(y+z/sqrt(2)),m);
End;
(*************************************************)
{thu tuc ve duong cong theo thuat toan CASTELEJ}
PROCEDURE ve;
Var
i,j : integer;
BEGIN
for i:=0 to l do
Begin
xi[i,0]:=x[i];
yi[i,0]:=y[i];
zi[i,0]:=z[i];
End;
u:=0;
while u<=1.01 do
Begin
for j:=1 to l do
Begin
for i:=j to l do
Begin
xi[i,j]:=(1-u)*xi[i-1,j-1]+u*xi[i,j-1];
yi[i,j]:=(1-u)*yi[i-1,j-1]+u*yi[i,j-1];
zi[i,j]:=(1-u)*zi[i-1,j-1]+u*zi[i,j-1];
End;
End;
put_pixel(round(xi[i,j]),round(yi[i,j]),round(zi[i,j]),WHITE);
u:=u+0.001
End;
END;
(*************************************************)
{-------------Chuong Trinh Chinh------------}


























