Tªn bµi so¹n :
Hµm sè y = sinx
( TiÕt PPCT : 01 )
A. Môc tiªu :
1. VÒ kiÕn thøc : Gióp häc sinh
•HiÓu kh¸i niÖm c¸c hµm sè y = sinx , y = cosx . Trong ®ã x
lµ sè thùc vµ lµ sè ®o ra®ian cña gãc ( cung ) lîng gi¸c
•N¾m ®îc c¸c tÝnh chÊt cña hµm sè y = sinx : TËp x¸c ®Þnh ;
TÝnh ch½n – lÎ ; TÝnh tuÇn hoµn ; TËp gi¸ trÞ
•BiÕt dùa vµo chuyÓn ®éng cña ®iÓm trªn ®êng trßn lîng gi¸c
vµ trªn trôc sin ®Ó kh¶o s¸t sù biÕn thiªn , råi thÓ hiÖn
sù biÕn thiªn ®ã trªn ®å thÞ
2. VÒ kü n¨ng : Gióp häc sinh
•BiÕt xÐt sù biÕn thiªn , vÏ ®å thÞ hµm sè y = sinx
3. VÒ t duy – Th¸i ®é :
•RÌn t duy l«gÝc
•TÝch cùc , høng thó trong nhËn thøc tri thøc míi
B. ChuÈn bÞ cña thÇy vµ trß :
•ChuÈn bÞ cña gi¸o viªn : Gi¸o ¸n – PhÊn mµu - §Ìn chiÕu
•ChuÈn bÞ cña häc sinh : S¸ch gi¸o khoa – B¶ng phô ( ®äc
tríc bµi häc )
C. Ph ¬ng ph¸p d¹y häc :
•Gîi më vÊn ®¸p – Ho¹t ®éng nhãm
D. TiÕn tr×nh d¹y häc :
1. æn ®Þnh líp
2. §Æt vÊn ®Ò vµo bµi míi : Tõ kiÕn thøc lîng gi¸c ®∙ ®îc häc ,
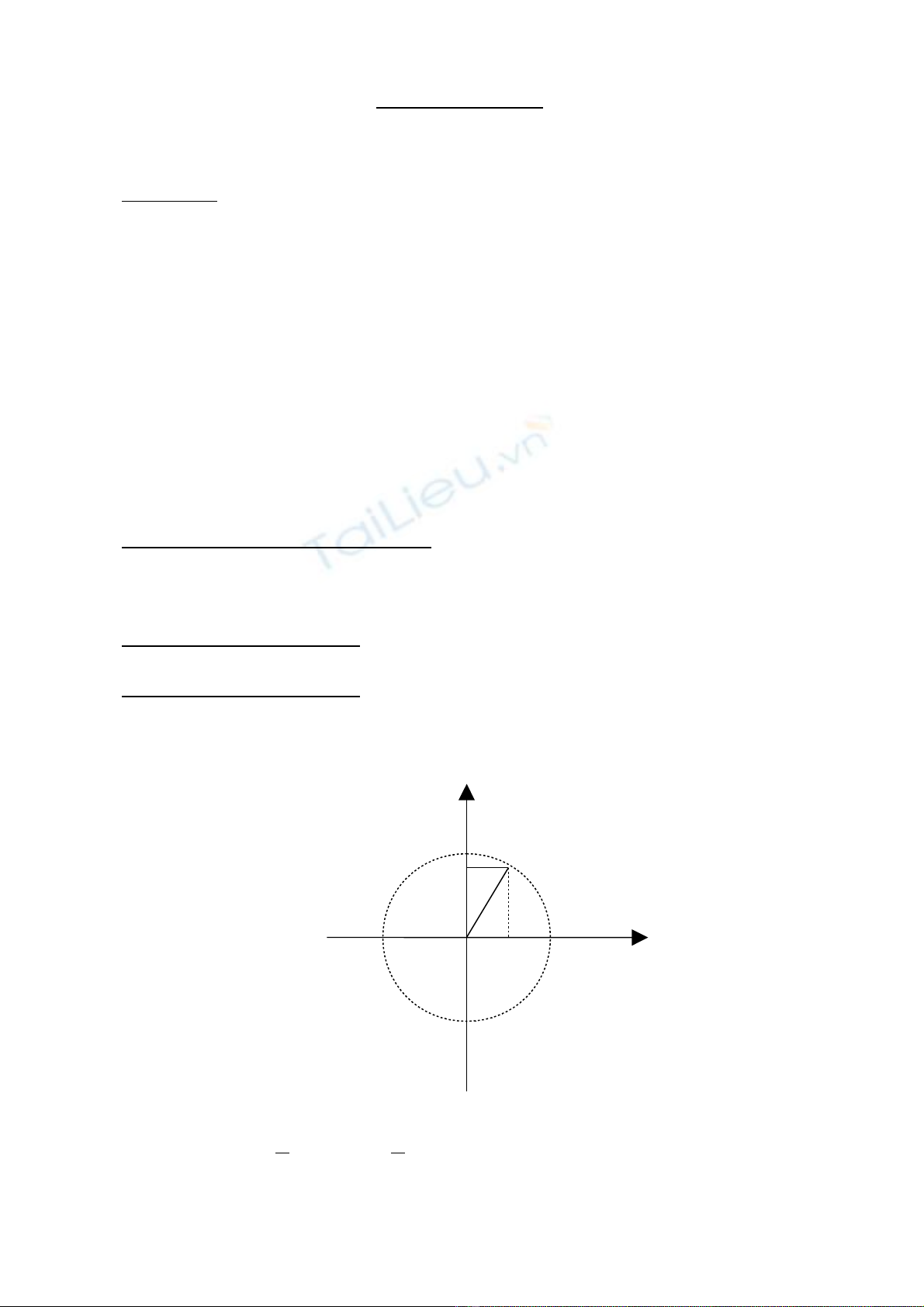
dùa vµo h×nh vÏ
H∙y chØ ra c¸c ®o¹n th¼ng cã ®é dµi ®¹i sè b»ng sinx , b»ng
cosx . TÝnh sin
2
π
; cos(-
4
π
) ; cos2
π
M
A
B
A’
H
K
Trlêi :
OK
= sinx ;
OH
= cosx ; sin
2
π
= 1 ; cos(-
4
π
) =
2
2
; cos2
= 1
* NÕu ta thay ®æi sè thùc x , x sè ®o ra®ian cña gãc ( cung )
lîng gi¸c th×
OK
,
OH
sÏ thay ®æi nh thÕ nµo ? H«m nay chóng
ta sÏ häc bµi häc ®Çu tiªn cña ch¬ng hµm sè lîng gi¸c
Bµi 1: Hµm sè y = sinx
Ho¹t ®éng 1: §Þnh nghÜa hµm sè y = sinx ; y = cosx
Ho¹t ®éng cña
thÇy
Ho¹t ®éng cña trß Néi dung ghi b¶ng
* PhÐp ®Æt t¬ng
øng víi mçi sè
thùc x vµ sin
( cos) cña gãc
lîng gi¸c cã sè
®o ra®ian b»ng x
nãi lªn ®Òu g× ?
* Nghe , hiÓu vµ
trlêi c©u hái
a. §Þnh nghÜa:
sin : R
→
R
cos : R
→
R
x
sinx
x
x
cosx
* Nãi ®Õn hµm sè
lµ nãi ®Õn c¸c
tÝnh chÊt cña
hµm sè . H∙y xÐt
tÝnh ch½n – lÎ
cña hµm sè y =
sinx ; y = cosx
vµ nhËn d¹ng ®å
thÞ cña mçi hµm
sè
* Häc sinh lªn
b¶ng chøng minh vµ
kÕt luËn
TÝnh ch½n – lÎ cña hµm sè :
*
∀
x
∈
R : sin(-x) = sinx
VËy hµm sè y = sinx lµ mét
hµm sè lÎ , nªn cã ®å thÞ
®èi xøng nhau qua gèc to¹
®é
*
∀
x
∈
R : cos(-x) = cosx
VËy hµm sè y = cosx lµ mét
hµm sè ch½n, nªn cã ®å thÞ
®èi xøng nhau qua trôc tung
Ho¹t ®éng 2: TÝnh chÊt tuÇn hoµn cña c¸c hµm sè y = sinx ; y =
cosx
Ho¹t ®éng cña
thÇy
Ho¹t ®éng cña trß Néi dung ghi b¶ng
* Ngoµi tÝnh
ch½n – lÎ cña
hµm sè mµ ta võa
míi ®îc «n . Hµm
sè lîng gi¸c cã
thªm mét tÝnh
chÊt n÷a , ®ã lµ
tÝnh tuÇn hoµn .
Dùa vµo s¸ch
gi¸o khoa h∙y
ph¸t biÓu tÝnh
* Nghe , hiÓu vµ
trlêi c©u hái
Do víi mäi x :
sin(x + 2
) = sin
x =
OK
cos(x + 2
π
) =
cosx =
OH
b.TÝnh chÊt tuÇn hoµn cña
c¸c hµm sè y=sin(x);
y=cos(x):
Ta cã : Sin(x+2
π
) = sinx
VËy : Hµm sè y = Sinx tuÇn
hoµn víi chu kú T=2
π
.
T¬ng tù : hµm sè y = cosx
tuÇn hoµn víi chu kú T=2
.
tuÇn hoµn cña
hµm sè y =
sinx ; y = cosx
* H∙y cho biÕt ý
nghÜa cña tÝnh
tuÇn hoµn hµm sè
* Nghe , hiÓu vµ
trlêi c©u hái
* Mçi khi biÕn sè ®îc céng
thªm 2
th× gi¸ trÞ cña c¸c
hµm sè ®ã l¹i trë vÒ nh cò.
Ho¹t ®éng 3: Sù biÕn thiªn vµ ®å thÞ hµm sè y = sinx
Ho¹t ®éng cña
thÇy
Ho¹t ®éng cña trß Néi dung ghi b¶ng
* Dïng ®Ìn chiÕu
chiÕu lªn b¶ng
®å thÞ hµm sè
hµm sè y =
sinx
∈∀x
[-
π
,
π
].
*Dïng ®êng trßn
lîng gi¸c.
H∙y cho biÕt
khi ®iÓm M
chuyÓn ®éng mét
vßng theo híng +
xuÊt ph¸t tõ
®iÓm A’ th× hµm
sè y = sinx biÕn
thiªn nh thÕ
nµo? Hay nãi mét
c¸ch cô thÓ th×
hµm sè t¨ng,
gi¶m trªn nh÷ng
kho¶ng nµo?
Do sin x =
OK
Nªn :
*
2
,(
π
π
−−∈∀x
) : hµm
sè gi¶m
*
2
,
2
(
ππ
−−∈∀x
): hµm
sè t¨ng.
*
),
2
(
π
π
∈∀x
: hµm sè
gi¶m
c.Sù biÕn thiªn vµ ®å thÞ
hµm sè y=sinx.
XÐt hµm sè y=sinx
],[
ππ
−∈∀x
* Hµm sè y = sinx gi¶m trªn
kho¶ng (-
2
;
π
π
−
)
∪
(
);
2
π
π
.
* Hµm sè y = sinx t¨ng lªn
kho¶ng (
2
;
2
ππ
−
)
* Dùa vµo tÝnh
t¨ng gi¶m cña
hµm sè y = sinx
],[
ππ
−∈∀x
. H∙y
lËp b¶ng biÕn
thiªn cña hµm
sè.
* Nghe , hiÓu vµ
trlêi c©u hái B¶ng biÕn thiªn :
( Tr×nh chiÕu ®å
thÞ hµm sè y =
sinx )
* Quan s¸t ®å
* Nghe , hiÓu vµ
trlêi c©u hái
§å thÞ : ( Sgk )
x
y=sinx
0
-1
0
1
0
-
-
2
π
0 -
2
π
thÞ hµm sè y =
sinx . H∙y cho
biÕt tËp gi¸ trÞ
cña hµm sè
3. Cñng cè : ( Th¶o luËn theo nhãm råi ®a ra c©u tr¶ lêi )
C©u1: KÕt luËn nµo sau ®©y sai ?
A. y = sinx.cos2x lµ hµm sè lÎ
B. y = sinx.sin2x lµ hµm sè ch½n
C. y = x + sinx lµ hµm sè lÎ
D. y = x + cosx lµ hµm sè ch½n
KQ: D
C©u 2: Khi x thay ®æi trong kho¶ng (
4
5
π
;
4
7
π
) th× y = sinx lÊy
mäi gi¸ trÞ thuéc
A.
1;
2
2
B.
−− 2
2
;1
C.
−0;
2
2
D.
[ ]
1;1−
KQ: B
C©u 3: Gi¸ trÞ bÐ nhÊt cña y = sinx + sin(x +
3
2
π
) lµ
A. – 2 B.
2
3
C. – 1 D. 0
KQ: C
C©u 4: TËp gi¸ trÞ cña hµm sè y = 2sin2x + 3 lµ :
A. [0;1] B. [2;3] C. [-2;3] D. [1;5]
KQ: D
4. DÆn dß :
1. §äc phÇn sù biÕn thiªn vµ ®å thÞ cña hµm sè y = cosx ; §Þnh
nghÜa c¸c hµm sè y = tanx ; y = cotx
2. Lµm bµi tËp 1a ; 2a ; 2b ; 3b ; 3c
* PhÇn rót kinh nghiÖm sau d¹y: