zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Khoa Học Tự Nhiên

Giải bài toán người du lịch qua phép dẫn về bài toán chu trình Hamilton

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:7

Báo xấu

16
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài viết Giải bài toán người du lịch qua phép dẫn về bài toán chu trình Hamilton giới thiệu một thuật toán hiệu quả để giải quyết bài toán trên theo cách dẫn nó về bài toán chu trình Hamilton với thuật toán tìm chu trình Hamilton được đề xuất.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giải bài toán người du lịch qua phép dẫn về bài toán chu trình Hamilton

TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH Giải bài toán ngƣời du lịch qua phép dẫn về bài toán chu trình Hamilton Nguyễn Thị Thúy Chinh*, Nguyễn Huy Hoàng Trường Đại học Công nghiệp Quảng Ninh *E-mail: nguyenthuychinh86qui@gmail.com Tóm tắt: Bài toán người du lịch được nhiều người biết đến với độ khó và phức tạp, đặc biệt với trường hợp có dữ liệu đầu vào lớn. Giải thuật láng giềng gần nhất là một trong các giải thuật heuristic được áp dụng để giải bài toán người du lịch trong trường hợp với dữ liệu đầu vào lớn. Việc tìm ra một thuật toán heuristic hiệu quả hơn vẫn là một trong những hướng nghiên cứu được nhiều nhà khoa học quan tâm. Bài báo giới thiệu một thuật toán hiệu quả để giải quyết bài toán trên theo cách dẫn nó về bài toán chu trình Hamilton với thuật toán tìm chu trình Hamilton được đề xuất. Từ khoá: Bài toán người du lịch; Bài toán Hamilton; Chu trình Hamilton; Thuật toán tham lam 1. ĐẶT VẤN ĐỀ Bài toán người du lịch (Travelling Salesman Problem - TSP) là bài toán có phát biểu đơn giản nhưng lại được đánh giá là một trong những bài toán kinh điển và khó trong trường hợp tổng quát với không gian dữ liệu đầu vào lớn. Nó được đánh giá là khó bởi các thuật toán hiệu quả nhất lại có thời gian xử lý tăng dần theo cấp số nhân của n, hay độ phức tạp thuật toán tăng theo hàm số mũ [3]. Có rất nhiều cách giải quyết bài toán này như thuật toán vét cạn, thuật toán người láng giềng gần nhất, kỹ thuật nhánh cận, nhưng mới chỉ hiệu quả với các bộ dữ liệu nhỏ. Trong khuôn khổ bài báo này, tôi xin giới thiệu một phương pháp giải bài toán người du lịch bằng cách dẫn về bài toán chu trình Hamilton, với thuật toán tìm chu trình Hamilton được đề xuất có thể cải thiện hiệu quả giải quyết bài toán với bộ dữ liệu lớn hơn. 2. GIỚI THIỆU BÀI TOÁN NGƯỜI DU LỊCH VÀ BÀI TOÁN CHU TRÌNH HAMILTON 2.1. Bài toán ngƣời du lịch 2.1.1. Phát biểu bài toán người du lịch Bài toán người du lịch (Travelling Salesman Problem - TSP) [4] là một bài toán trong lĩnh vực tối ưu tổ hợp được nhiều người biết đến. Nội dung của nó khá đơn giản, nó được phát biểu như sau: Một người du lịch xuất phát từ thành phố của anh ta, anh ta muốn tìm một đường đi đi qua tất cả các thành phố, mỗi thành phố đi đúng một lần và sau đó trở về thành phố ban đầu sao cho chi phí là ít nhất. Tên gọi bài toán người du lịch mang tính chất tượng trưng, nó dùng để gọi chung cho các bài toán có mô hình toán học như trên mặc dù phát biểu có nội dung khác, chẳng hạn bài toán tìm chu trình sản xuất cho một nhà máy hóa chất sao cho chi phí xúc rửa các thiết bị (như bể chứa, ống dẫn, ...), mỗi khi chuyển từ loại hóa chất này sang loại hóa chất khác của chu trình là ít nhất. Trong một số ứng dụng khác, khái niệm thành phố có thể thay đổi thành khách hàng, các mảnh DNA trong gen, các điểm hàn trên bảng mạch và khái niệm chi phí có thể biểu diễn bởi thời gian du lịch hay khoảng cách, hay giống như sự so sánh giữa các mảnh DNA với nhau [8]. Trong lý thuyết của độ phức tạp tính toán, bài toán TSP là bài toán khó, thuộc lớp NP- Complete. Nên nó không có giải thuật hiệu quả nào có thể áp dụng cho mọi trường hợp, đặc biệt với các trường hợp có số lượng thành phố lớn. 250 Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH Bài toán TSP có thể phát biểu dưới ngôn ngữ đồ thị: Cho đồ thị G = (V, E), trong đó V là tập các đỉnh, E là tập các cạnh, mỗi cạnh được gán trọng số. Tìm chu trình Hamilton có tổng trọng số là nhỏ nhất. Trong đó, các đỉnh của đồ thị tương ứng với các thành phố và các cạnh thì tương ứng với đường nối giữa các thành phố, trọng số gán cho mỗi cạnh là chi phí di chuyển giữa hai thành phố. Một đường đi trong bài toán TSP là một chu trình Hamilton trên đồ thị và một lời giải tối ưu của bài toán là chu trình Hamilton ngắn nhất. Việc tìm chu trình Hamilton trong một đồ thị đầy đủ là dễ, nên các bài toán mà không phải hai thành phố nào cũng được nối với nhau có thể được chuyển đổi thành đồ thị đầy đủ, bằng cách thêm những cạnh có độ dài lớn giữa các thành phố này, những cạnh này sẽ không xuất hiện trong chu trình tối ưu. 2.1.2. Giải bài toán TSP với thuật toán người láng giềng gần nhất Khi dữ liệu đầu vào bài toán TSP có kích thước nhỏ, thì ưu tiên sử dụng các thuật toán giải chính xác cho kết quả nhanh và duy nhất như thuật toán vét cạn. Nhưng khi dữ liệu đầu vào lớn, thì thuật toán giải chính xác không còn hiệu quả do thời gian xử lý quá lâu. Lúc này, người ta quan tâm và ưu tiên tới hiệu suất tính toán và khi đó thuật toán heuristic được sử dụng. Tuy không thể đưa ra kết quả tối ưu nhất nhưng sai số so với giải pháp tối ưu nhất không nhiều, có thể chấp nhận được. Thuật toán láng giềng gần nhất là một trong những thuật toán heuristic như vậy. Giải thuật người láng giềng gần nhất (Nearest Neighbour - NN) (hay còn gọi là giải thuật tham lam – Greedy Algorithm) [6] là giải thuật cho người du lịch chọn thành phố gần nhất chưa thăm trong lần di chuyển tiếp theo. Thuật toán này bắt đầu từ một thành phố tùy ý, duyệt lần lượt tất cả các cạnh kề với nó rồi lựa chọn đỉnh có cạnh nối với đỉnh hiện tại đang xét có chi phí là thấp nhất để đưa vào hành trình. Lại tiếp tục xét các đỉnh kề với đỉnh mới đưa vào hành trình, như vậy cho đến khi không còn đỉnh nào để xét nữa thì thuật toán dừng. Các đỉnh đưa vào hành trình cần thỏa mãn 2 yêu cầu: - Không tạo thành một chu trình thiếu (không đi qua đủ n đỉnh). - Không tạo thành một đỉnh có nhiều hơn hai cạnh xuất phát từ một đỉnh, do yêu cầu của bài toán là mỗi thành phố chỉ được đến một lần: một lần đến và một lần đi. Độ phức tạp của thuật toán là O(n2) Tuy nhiên, khi áp dụng thuật toán này sẽ có lúc phải đưa vào hành trình đang xét một cạnh có chi phí rất cao, do các cạnh có chi phí thấp nối với đỉnh hiện tại đang xét đã được thăm. Với trường hợp này, giải pháp tìm được không tối ưu. 2.2. Bài toán chu trình Hamilton Bài toán chu trình Hamilton là bài toán xác định xem với một đồ thị G=(V, E) cho trước có chứa một chu trình Hamilton hay không? Cho đồ thị G, chu trình bắt đầu từ một đỉnh v nào đó, qua tất cả các đỉnh còn lại mỗi đỉnh đúng một lần rồi quay trở về v được gọi là chu trình Hamilton. Bài toán HC trên đã được chứng minh là bài toán NPC [7]. Thuật toán tối ưu cho bài toán này sẽ là thuật toán tìm đường đi ngắn nhất cho chu trình Haminton. Hiện nay, các nhà khoa học chưa đưa ra được các quy tắc cần và đủ để kiểm tra xem một đồ thị có là Hamilton hay không. Để giải quyết bài toán này, có thể sử dụng thuật toán vét cạn: Giả sử G = (V, E) là đồ thị vô hướng gồm n đỉnh với tập đỉnh V = {v1, v2, ..., vn}, nếu G là đồ thị Hamilton thì sẽ có chu trình Hamilton có dạng: v1  vi1  vi2  vi3... vi n-1  v1, với {i1, i2, ..., in-1} là một hoán vị của tập hợp {2, 3, ..., n}. Từ đó, ta có một thuật toán hiển nhiên là: Đặt Z = {vi1, vi2, vi3, …} là dãy đỉnh tương ứng trong hoán vị của tập {2, 3, …, n} ta kiểm tra xem Z có tạo nên chu trình hay không, tức là phải kiểm tra (n-1)! tập Z khác nhau. Ta dễ dàng nhận thấy với thuật toán vét cạn thì độ phức tạp của nó không khả thi khi n chỉ từ 20, 30 đỉnh trở lên. Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022 251
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH Việc nghiên cứu tìm ra thuật toán hiệu quả, để xác định xem một đồ thị có chứa chu trình Hamilton hay không vẫn đang là một thách thức lớn đối với các nhà khoa học. Một số nhà nghiên cứu đã đề xuất các thuật toán Heuristic (nhờ vào việc vận dụng các thuật toán thông minh nhân tạo, mạng neural, thuật toán gen, ...), để giải quyết gần đúng các bài toán Hamilton. 3. GIẢI BÀI TOÁN NGƯỜI DU LỊCH BẰNG PHÉP DẪN VỀ BÀI TOÁN CHU TRÌNH HAMILTON Dễ thấy bài toán người du lịch chính là bài toán chu trình Hamilton nhưng với điều kiện tổng các cạnh của chu trình Hamilton này nhỏ nhất có thể. Theo định lý Dirac: Định lý 4 (Dirac - 1952): Nếu G là một đơn đồ thị có n đỉnh và mọi đỉnh của G đều n có bậc không nhỏ hơn thì G là một đồ thị Hamilton. 2 3.1. Thuật toán dẫn bài toán ngƣời du lịch về bài toán chu trình Hamilton Đầu tiên, ta loại bỏ các cạnh dài nhất của đồ thị so với đồ thị gốc ban đầu sao cho đồ thị thu được phải bảo đảm vẫn còn chu trình Hamilton. Áp dụng định lý Dirac, quá trình bỏ n cạnh phải bảo đảm đồ thị thu được có bậc mỗi đỉnh không ít hơn . Theo định lý Dirac thì 2 đồ thị thu được vẫn có chu trình Hamilton. Sau đó, ta tìm chu trình Hamilton trong đồ thị mới và kết quả thu được sẽ là chu trình tương đối tối ưu.  Ý tƣởng: n Giả sử đồ thị G với n đỉnh là v0, v1, …, vn-1; thỏa mãn deg(v)  . Thuật toán sau đây 2 sẽ xác định một chu trình Hamilton C của G trong thời gian đa thức. 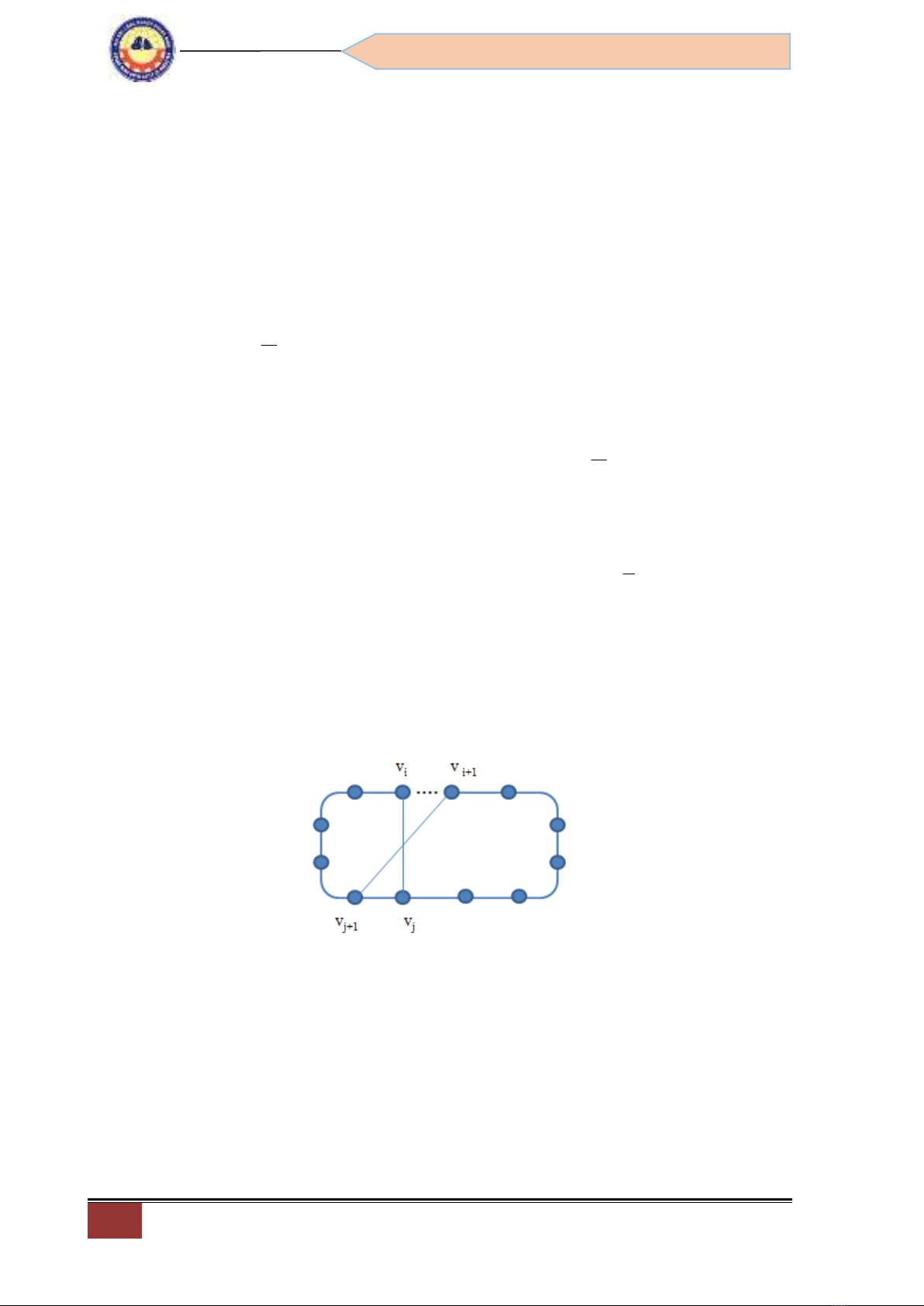Ý tưởng của thuật toán là: Xuất phát từ một hoán vị C = (v0, v1,…, vn-1, vn = v0) tùy ý, ta gọi (vi, vi+1) là một lỗ hổng của C nếu 2 đỉnh vi và vi+1 không kề nhau (hình 1). Nếu vivj và vi+1vj+1 là cạnh thì chúng được gọi là bắt chéo nhau (hình 1). Ta sẽ biến đổi C liên tục sao cho trong mỗi bước điều chỉnh số các lỗ hổng thu được giảm đi ít nhất 1 đỉnh. Như vậy, sau hữu hạn bước ta sẽ thu được một hoán vị không có lỗ hổng nào. Hoán vị này là một chu trình Hamilton. Hình 1. Lỗ hổng và cung bắt chéo Thuật toán dựa trên chu trình Hamilton có thể áp dụng cho bài toán TSP dưới dạng biểu diễn đồ thị G = (M, K) là đồ thị có đầy đủ có trọng số, trong đó M là tập hợp của n = |M| nút (thành phố), K = {(i, j)| (i, j)  M  M} là tập hợp tất cả các cung của đồ thị. Mỗi cung (i, j) được gán một trọng số dij để biểu diễn khoảng cách giữa hai thành phố i và j. Tập giải pháp của vấn đề chính là tập các hành trình khả dụng bắt đầu từ thành phố xuất phát đến thành phố đích. Điều này hoàn toàn có thể, bởi vì bất cứ đường nào mà đi qua tất cả các đỉnh, mỗi đỉnh đúng một lần không lặp lại thì được xem như một hành trình khả thi. Bài toán TSP trở thành bài toán tìm chu trình Hamilton có độ dài ngắn nhất trên đồ thị G. Khi n lớn ta không thể tìm được lời giải tối ưu bằng các thuật toán vét cạn, hướng đi giải quyết bài toán là tìm các lời giải xấp xỉ tối ưu bằng các thuật toán heuristic, hoặc các thuật toán tiến hóa. 252 Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH Thuật toán đề xuất mới (thuật toán dựa trên chu trình Hamilton) được xây dựng bằng cách áp dụng các thủ tục xây dựng đơn giản sau đây: (1) Lựa chọn một thành phố xuất phát. (2) Áp dụng điều kiện của định lý Dirac và hoán vị các lỗ hổng để sau hữu hạn bước ta sẽ thu được một hoán vị không có lỗ hổng nào. Hoán vị này là một chu trình Hamilton. (3) Quay trở lại thành phố ban đầu. Sau khi thuật toán này đã hoàn thành hành trình thì sẽ để lại đường đi trên hành trình đã thực hiện.  Phát biểu bài toán: Input: Đồ thị G = (V, E) với n đỉnh thỏa mãn deg(v) ≥ . Output: Tìm đường đi tối ưu nhất.  Mã giả của thuật toán: Begin Khởi tạo một hoán vị C các đỉnh một cách ngẫu nhiên; While vivi+1  E(G) do Begin Đánh số các đỉnh của C lần lượt C = (v0, v1,…, vn-1, vn = v0); Tìm số i nhỏ nhất sao cho vi không kề với vi+1; Nếu C không có lỗ hổng nào thì dừng; Tìm j nhỏ nhất sao cho cạnh vivj bắt chéo cạnh vi+1vj+1; C:= (vivjvj-1 …vi+1vj+1 vj+2 …vi-1vi); End; End. Cách xác định thành phố kế tiếp để đi Giả sử V={v1, v2, …, vm} là tập các láng giềng của u và p1, p2, …, pm là xác suất lựa chọn đỉnh tiếp theo từ u của tương ứng v1, v2, …, vm. Ta có: m sum   pi  1 (1) i 1 Nghĩa là chắc chắn chọn một trong các đỉnh trên để đi tiếp. Để đảm bảo ưu thế của những đỉnh có xác suất lớn, nhưng vẫn đảm bảo cơ hội của các đỉnh có xác suất thấp hơn người ta sinh ra một số ngẫu nhiên k thuộc khoảng (0, sum] rồi chọn i nhỏ nhất sao cho: i p j 1 j k (2) Sau khi khởi tạo các tham số và hoán vị C, thuật toán đa thức lặp thông qua một vòng lặp chính: đầu tiên là xác định tất cả các lỗ hổng có thể có của hành trình, sau đó là cải thiện kết quả bằng cách điều chỉnh số các lỗ hổng thu được giảm đi ít nhất 1 đỉnh, và cuối cùng là cập nhật lại đường đi của hành trình đã đi qua để phản ánh kinh nghiệm tìm kiếm của giải thuật. 3.2. Tính đúng đắn và độ phức tạp của thuật toán  Tính đúng đắn của thuật toán Ta chứng minh rằng với một lỗ hổng vivi+1 thì sẽ luôn tồn tại vj để vivj bắt chéo vi+1vj+1. Thật vậy: Đặt S = {vk : vk kề vi} và T = {vk: vk+1 kề vi+1}. Khi đó: deg(vi) = |S| và deg(vi+1) = |T|. Vì vi không kề vi+1 nên theo giả thiết ban đầu có deg(vi) + deg(vi+1) ≥ n, do đó |S| + |T| ≥ n. Vì vi không thuộc tập T  S nên |T  S| ≤ n - 1. Từ |T  S| = |T| + |S| - |T  S| ≥ n – (n - 1) = 1 suy ra (T  S)   . Chọn vj  (T  S), ta có vi kề vj và vi+1 kề vj+1. Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022 253
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH Sau bước điều chỉnh lại hoán vị C ở bước 2 thì số lỗ hổng của C sẽ giảm đi ít nhất 1 đỉnh, sau không quá n bước lặp thì C sẽ không còn lỗ hổng nào, hay khi đó C là chu trình Hamilton, thuật toán sẽ dừng lại.  Độ phức tạp của thuật toán Do số lỗ hổng của một hoán vị không quá n cho nên số vòng lặp của bước 2 là không quá n. Việc tìm chỉ số i và j (xác định cung chéo nhau) bước 2 đều không quá n phép toán. Điều chỉnh hoán vị C ở mục bước 2 và việc đồng nhất chỉ số cũng không cần quá O(n) phép toán. Do đó, thuật toán sẽ kết thúc sau không quá O(n2) phép toán. 4. CÀI ĐẶT CHƯƠNG TRÌNH THỬ NGHIỆM Xây dựng chương trình thử nghiệm giải bài toán người du lịch với 2 thuật toán: thuật toán tham lam và thuật toán dựa trên chu trình Hamilton. Ứng dụng được phát triển trên môi trường Visual Studio 2012 với ngôn ngữ sử dụng là C#. Chương trình sử dụng dữ liệu Eil51.tsp, Eil101.tsp trong thư viện TSPLib để đánh giá kết quả và so sánh kết quả với thuật toán tham lam. Chương trình được thử nghiệm trên máy tính có cấu hình Intel(R) Core(TM) i5-6200U CPU @ 2.30GHz, 4GB RAM, cài đặt hệ điều hành Windows 10 Pro 64-bit. Thử nghiệm 10 lần cho mỗi thuật toán dựa trên chu trình Hamilon và thuật toán tham lam trên 2 bộ dữ liệu thử nghiệm Eil51 và Eil101, sau đó so sánh các giá trị tối ưu nhất mà mỗi thuật toán tìm được trên cùng bộ dữ liệu 51 đỉnh và 101 đỉnh. Kết quả thực nghiệm được thể hiện trong bảng 1 và bảng 2 dưới đây. Bảng 1. Bảng kết quả giá trị tối ưu Bảng 2. Bảng kết quả giá trị tối ưu của của hành trình trong mỗi lần thực hiện hành trình trong mỗi lần thực hiện thuật thuật toán dựa trên chu trình Hamilton toán tham lam Dữ liệu Eil51 Eil101 Dữ liệu Eil51 Eil101 1 473.82 719.36 1 478 736.33 2 471.77 724.01 2 471.21 713.84 3 472.46 720.71 3 476.94 720.71 4 471.29 728.96 4 483.92 734.96 Lần 5 470.3 739.75 Lần 5 479.48 717.77 thực thực hiện 6 468.63 714.9 hiện 6 474.74 739.57 7 469.13 727.53 7 468.12 709.84 8 466.55 724.07 8 467.29 751.51 9 464.94 739.59 9 478 729.74 10 468.39 717.97 10 481.35 722.9 Trung bình 469.73 725.69 Trung bình 475.91 727.72 Cả hai thuật toán dựa trên chu trình Hamilon và thuật toán tham lam áp dụng cho bài toán người du lịch đều cho kết quả tốt. So sánh giá trị tối ưu trung bình của hai giải thuật trên cho cả hai bộ dữ liệu Eil51, Eil101 cho thấy thuật toán dựa trên chu trình Hamilon cho kết quả tối ưu hơn một chút, nhưng chênh lệch giữa hai kết quả là không nhiều. Tuy nhiên, cũng như thuật toán tham lam, hiệu quả của thuật toán dựa trên chu trình Hamilon cũng phản ứng rất nhạy với các thiết lập tham số đầu vào là số lượng ít các đỉnh. Ưu điểm của thuật toán dựa trên chu trình Hamilon so với thuật toán tham lam là thuật toán dựa trên chu trình Hamilton có thể giải quyết bài toán với số lượng đỉnh lớn hơn cho hiệu 254 Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH quả tốt hơn. Tuy nhiên, nhược điểm của thuật toán dựa trên chu trình Hamilon qua thử nghiệm cho thấy thời gian cho kết quả tối ưu của nó chậm hơn so với thuật toán tham lam. So sánh giá trị tối ƣu của thuật toán dựa trên 490 Giá trị 480 470 460 450 1 2 3 4 5 6 7 8 9 10 Lần thực hiện Thuật toán dựa trên chu trình Hamilton Hình 2. So sánh giá trị tối ưu của thuật toán dựa trên chu trình Hamilon và thuật toán tham lam trên bộ dữ liệu Eil51 So sánh giá trị tối ƣu của thuật toán dựa trên 760 750 Giá trị tối 740 730 720 710 700 690 680 1 2 3 4 5 6 7 8 9 10 Lần thực hiện Thuật toán dựa trên chu trình Hamilton Hình 3. So sánh giá trị tối ưu của 2 thuật toán dựa trên chu trình Hamilton và thuật toán tham lam trên bộ dữ liệu Eil101 5. KẾT QUẢ VÀ THẢO LUẬN Bài viết đã giới thiệu bài toán người du lịch và bài toán chu trình Hamilton, dẫn bài toán người du lịch về bài toán chu trình Hamilton. Tìm hiểu việc giải bài toán người du lịch với thuật toán tham lam và thuật toán dựa trên chu trình Hamilon. Xây dựng chương trình thực nghiệm thực hiện so sánh hiệu quả của hai thuật toán trên với bộ dữ liệu đầu vào Eil51 và Eil101. Với thuật toán dựa trên chu trình Hamilton đã trình bày trong bài viết, chúng ta có thể nghiên cứu áp dụng thuật toán này cho các bài toán tối ưu tổ hợp phức tạp khác. 6. KẾT LUẬN Việc tìm ra giải thuật hiệu quả cho việc giải quyết bài toán gười du lịch vẫn là một hướng mở cần được nghiên cứu. Giải bài toán gười du lịch bằng việc dẫn về bài toán chu trình Hamilton với thuật toán tìm chu trình Hamilton cũng là một phương pháp khá hiệu quả trong trường hợp với bộ dữ liệu đầu vào lớn, tuy nhiên thời gian thực hiện còn hơi chậm. Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022 255
TRƢỜNG ĐẠI HỌC CÔNG NGHIỆP QUẢNG NINH TÀI LIỆU THAM KHẢO [1]. Vũ Đình Hòa & Đỗ Trung Kiên (2007), Thuật toán và đánh giá độ phức tạp thuật toán, NXB ĐHSP, Hà Nội. [2]. Nguyễn Thị Thúy Chinh (2021), Bài giảng Toán rời rạc, Khoa Công nghệ thông tin Trường Đại học Công nghiệp Quảng Ninh. [3]. J.N. Macgregor, T. Ormerod (1996), Human performance on the traveling salesman problem. [4]. David S. Johnson, Lyle A. McGeoch, The Traveling Salesman Problem: A Case Study in Local Optimization. [5]. Christos Voudouris, Edward Tsang (1999), Guided local search and its application to the traveling salesman problem. [6]. Cormen, Leiserson, Rivest (1990), Introduction to Algorithms, Chương 16 "Greedy Algorithms", tr 329, MIT PRESS. [7]. M. V. N. N. C. David Joyner (2010), Algorithmic Graph Theory, Version 0.3. Melissa de Leon (1978), "A study of sufficient Conditions for Hamilton Cycle", Seton Hall University South Orange, New Jersey, USA, tr 184-186. [8]. http://en.wikipedia.org [9]. https://viblo.asia Solving the Traveler problem by transformation of the Hamilton cycle problem Thi Thuy Chinh Nguyen, Huy Hoang Nguyen Quang Ninh University of Industry Abstract: The Traveler problem is well known for its difficulty and complexity, especially in the case of large input data. The nearest neighbor algorithm is one of the heuristic algorithms applied to solve the Traveler problem in the case with large input data. Finding a more efficient heuristic algorithm is still one of the research directions that many scientists are interested in. The article introduces an effective algorithm to solve the above problem by referring it to the Hamilton cycle problem with the proposed Hamiltonian cycle finding algorithm. Keywords: The traveler problem, hamilton problem, hamilton cycle, greedy algorithm. 256 Kỷ yếu Hội nghị KHCN lần 7, tháng 5/2022

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.