Giới thiệu tài liệu
Bài giảng Lý thuyết đồ thị: Chương 4 của Tôn Quang Toại tập trung vào kiến thức, thuật toán và ứng dụng của Đồ thị Euler. Nội dung bao gồm định nghĩa, kiểm tra, và các thuật toán liên quan tới đồ thị này.
Đối tượng sử dụng
Nhà nghiên cứu, học sinh, và doanh nghiệp có quan tâm đến khoa học và công nghệ liên quan đến đồ thị
Nội dung tóm tắt
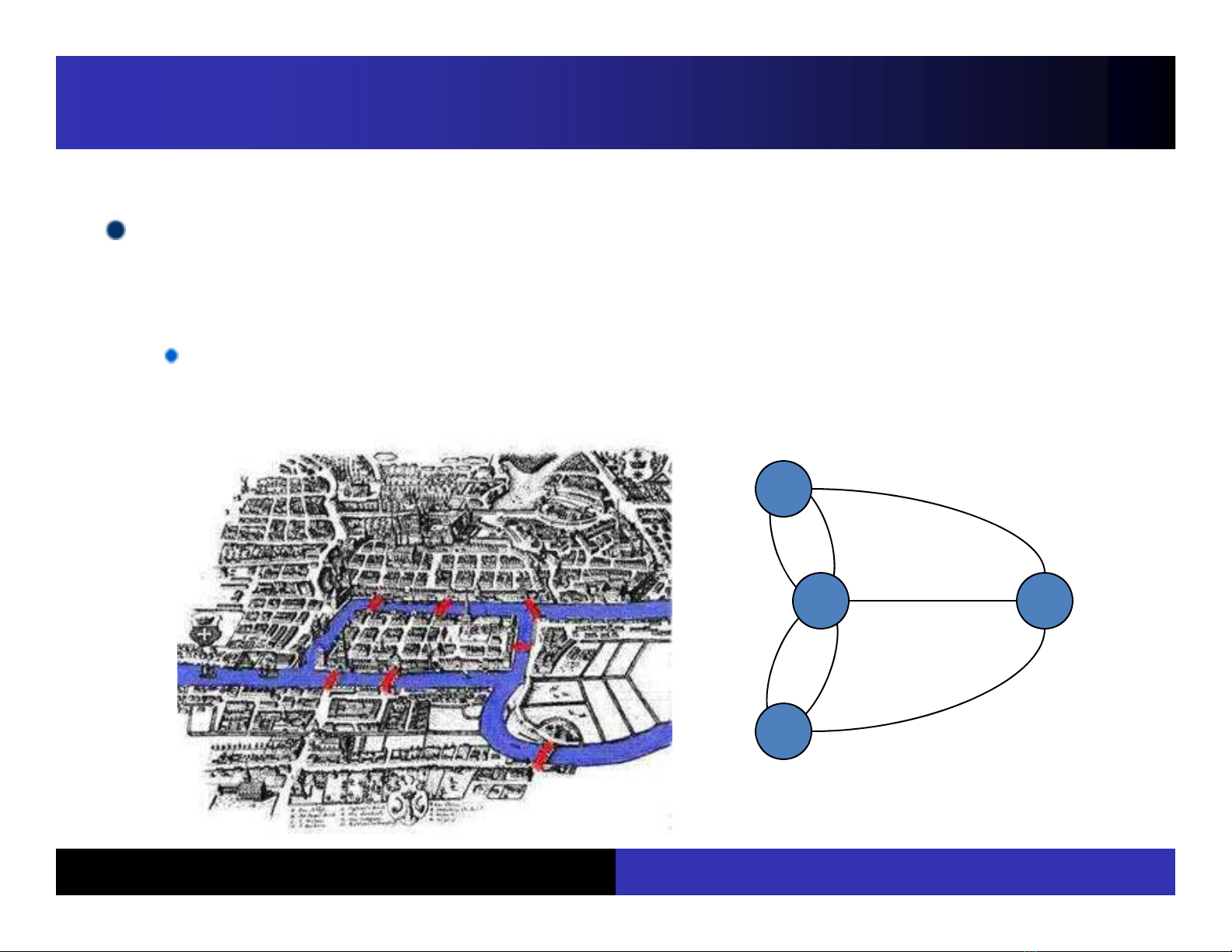
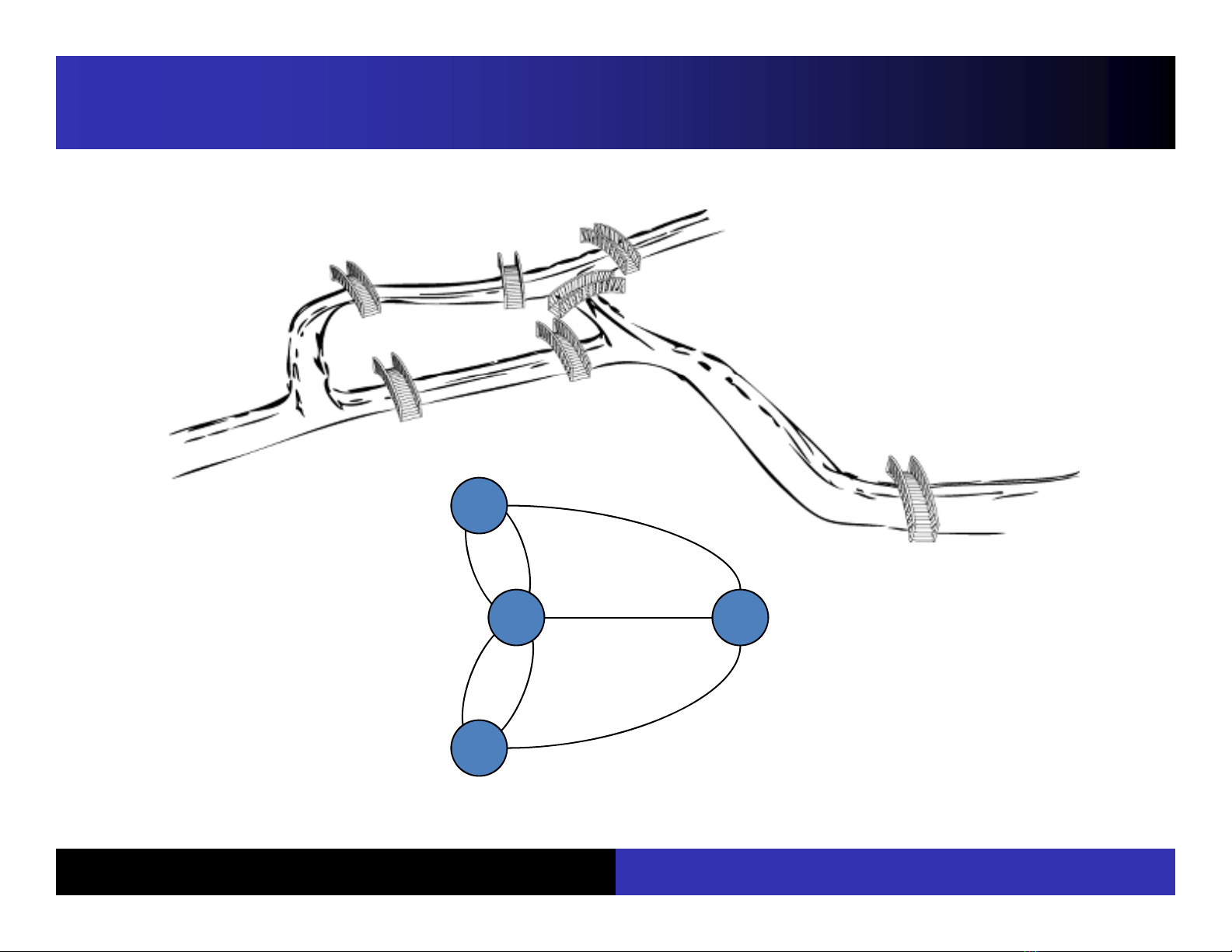
Chương Lý thuyết đồ thị: Chương 4 khẳng định rằng Đồ thị Euler là một chu trình qua tất cả các cạnh của đồ thị, mỗi cạnh chỉ đi qua 1 lần (định nghĩa). Đồ thị Euler có sẵn khi và chỉ khi đồ thị liên thông và bậc tất cả các đỉnh là chẵn. Thuật toán kiểm tra đồ thị Euler (IsEulerGraph()) được giới thiệu, có ba bước: kiểm tra tính liên thông, tính bậc của mọi đỉnh và kiểm tra số lẻ/chẵn của bậc của đỉnh. Các chu trình Euler có thể tìm được bằng cách áp dụng các thuật toán như Euler tour và DFS (Depth First Search). Bài giảng cũng giới thiệu Đồ thị Hamilton, một loại đồ thị khác có ý nghĩa lớn trong học tập và nghiên cứu đồ thị. Các chu trình Hamilton cần phải qua mọi cạnh của đồ thị, nhưng không bắt buộc phải qua tất cả các đỉnh. Quy tắc tìm kiếm chu trình Hamilton và thuật toán tìm chu trình Hamilton được giới thiệu, cũng như một cách áp dụng DFS để tìm chu trình này.
