Giâo trình Vật lý 2 Ths. Trương Thành
71
CHƯƠNG VII.
PHÂN CỰC ÁNH SÁNG
7.1. ÁNH SÁNG TỰ NHIÊN, ÁNH SÁNG PHÂN CỰC
7.1.1. ÁNH SÁNG TỰ NHIÊN
Ta biết rằng ánh sáng là sóng điện từ có hai vector đặc trưng là
H
và E
dao động luôn luôn vuông góc với nhau và vuông góc với phương truyền
sóng:
)/(2cos
)/(2cos
,
,
λγπ
λγπ
ytHH
ytEE
OtM
OtM
−=
−=
rr
r
r
Trong đó vector E đóng vai trò quan
trọng vì nó quyết định cường độ sáng
của ánh sáng.
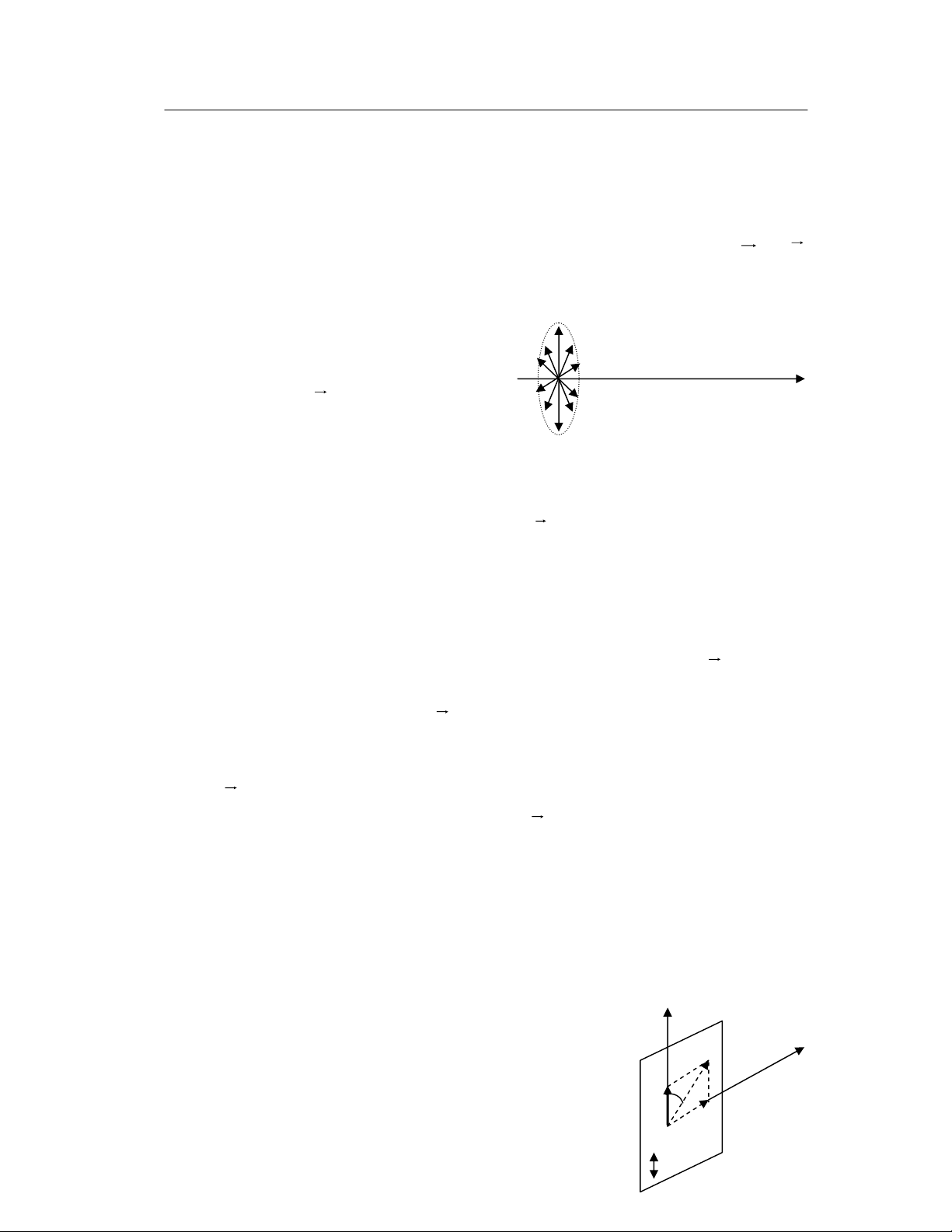
Ánh sáng tự nhiên là tổng hợp
của nhiều ánh sáng do các phân tử và nguyên tử phát ra một cách hỗn loạn
theo các phương khác nhau, bởi vậy vector E phân bố đều theo mọi phương
vuông góc với phương truyền (hình vẽ VII-1). Do vậy ta có định nghĩa:
Ánh sáng tự nhiên là ánh sáng mà vector cường độ điện trường của
sóng phân bố đều theo mọi phương vuông góc với phương truyền sóng.
7.1.2. ÁNH SÁNG PHÂN CỰC
Bằng một cách nào đó mà tạo ra được ánh sáng có vector E dao động
theo một phương nhất định thì ánh sáng đó gọi là ánh sáng phân cực hoàn
toàn. Nếu ánh sáng mà vector E chỉ mạnh lên theo một phương còn các
phương khác thì yếu đi gọi là ánh sáng phân cực một phần. Dụng cụ tạo nên
được ánh sáng phân cực gọi là máy phân cực hay Nicon. Mặt phẳng chứa
vector E và phương truyền gọi là mặt phẳng phân cực. Tóm lại là máy phân
cực chỉ trong suốt đối với tia sáng có vector E trùng với phương phân cực.
Ánh sáng phân cực hoàn toàn là ánh sáng mà vector cường độ điện
trường dao động theo một phương nhất định vuông góc với phương truyền
sóng.
Ánh sáng phân cực không hoàn toàn là ánh sáng mà vector cường độ
điện trường dao động mạnh lên ở một phương còn các phương khác thì yếu đi
nhưng không bằng không.
7.1.3. ĐỊNH LÝ MALUS
7.1.3.1. Giải thích hiện tượng phân cực
Hiện tượng phân cực được giải thích như sau:
mọi vector cường độ điện trường E đều được phân tích
H. VII-1
E
r
v
r
H. VII-2
E
r
ϕ
Giâo trình Vật lý 2 Ths. Trương Thành
72
thành hai thành phần, một phần song song với quang trục và một phần vuông
góc với quang trục. Phần song song với quang trục thì đi qua được máy phân
cực còn phần vuông góc với quang trục thì bị hấp thụ chính vì vậy mà sau
dụng cụ phân cực cường độ điện trường E chỉ có một phương duy nhất là
phương của quang trục:
ϕ
cos
0
EEpc
=
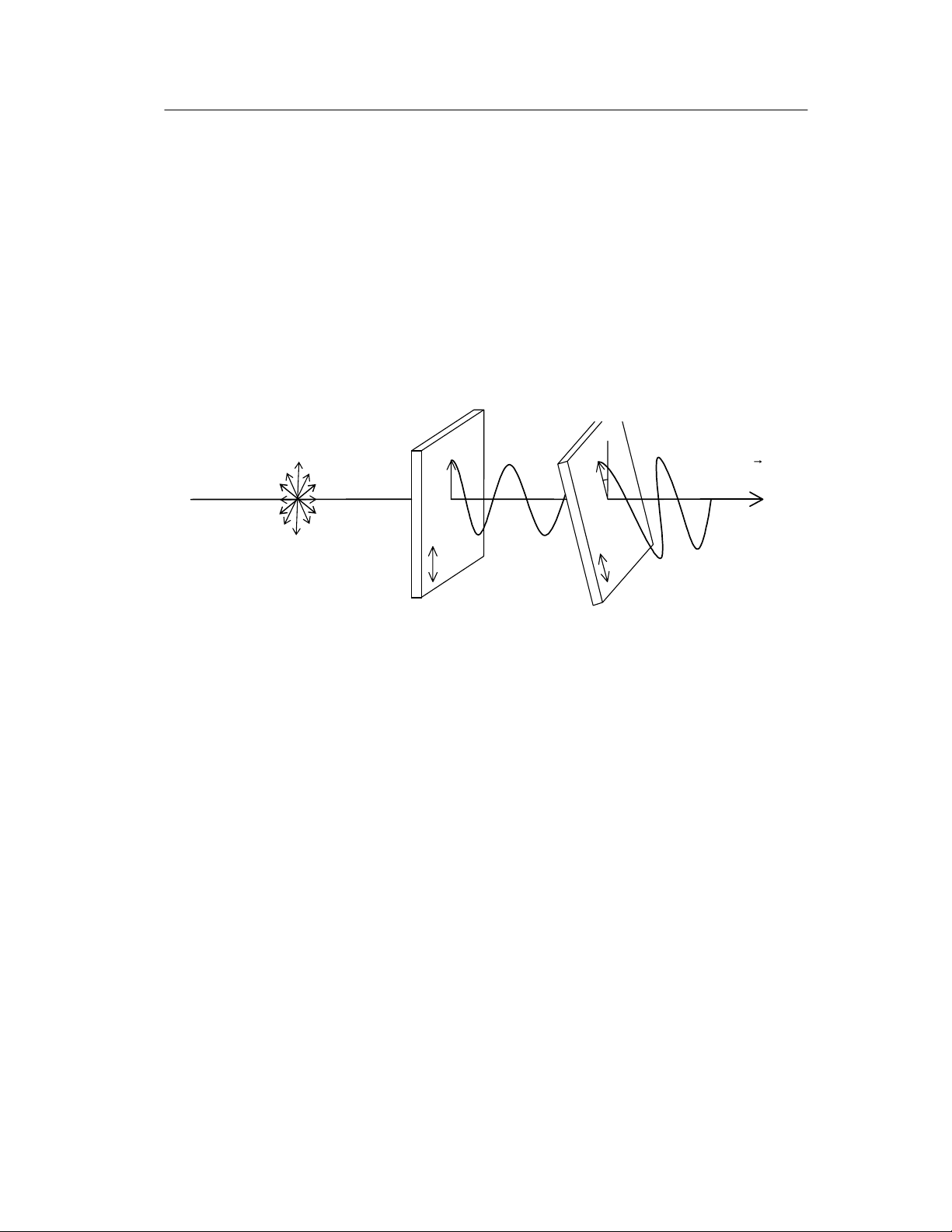
7.1.3.2. Định lý Malus
Trên đường đi của áng sáng tự nhiên ta đặt một máy phân cực có
phương quang trục là ∆1 thì sau máy phân cực ta được ánh sáng phân cực
theo phương ∆1. Tiếp theo sau ∆1 ta đặt thêm máy phân cực có phương phân
cực là ∆2 hợp với ∆1 một góc ϕ (hình vẽ) thì sự phân cực tiếp theo lại theo ∆2.
Nếu gọi E1 và E2 lần lượt là biên độ của của cường độ điện trường của
ánh sáng phân cực E1y và E2y sau hai bản phân cực thì dễ dàng thấy:
E
2 = E1 cos ϕ.
Còn cường độ sáng sau bản thứ 2 là I2:
I2 = E22 = E12cos2ϕ
Nhưng E12 =I1.
Nên; I2 = I1 cos2ϕ (VII-1).
Đây là một nội dung của định lý Malus
Định lý
Cường độ ánh sáng phân cực sau hai bản Tuamalin tỷ lệ thuận với
bình phương của cos của góc giữa hai quang trục của hai bản.
Trong đó:
- T1 gọi là bản phân cực ánh sáng
- T2 gọi là bản phân tích ánh sáng
E
2
E
1
∆
∆
2
ϕ
v
Hình VII-3
Giâo trình Vật lý 2 Ths. Trương Thành
73
7.2. SỰ PHÂN CỰC DO PHẢN
XẠ, HIỆN TƯỢNG LƯỠNG CHIẾT
7.2.1. SỰ PHÂN CỰC CỦA
ÁNH SÁNG DO PHẢN XẠ
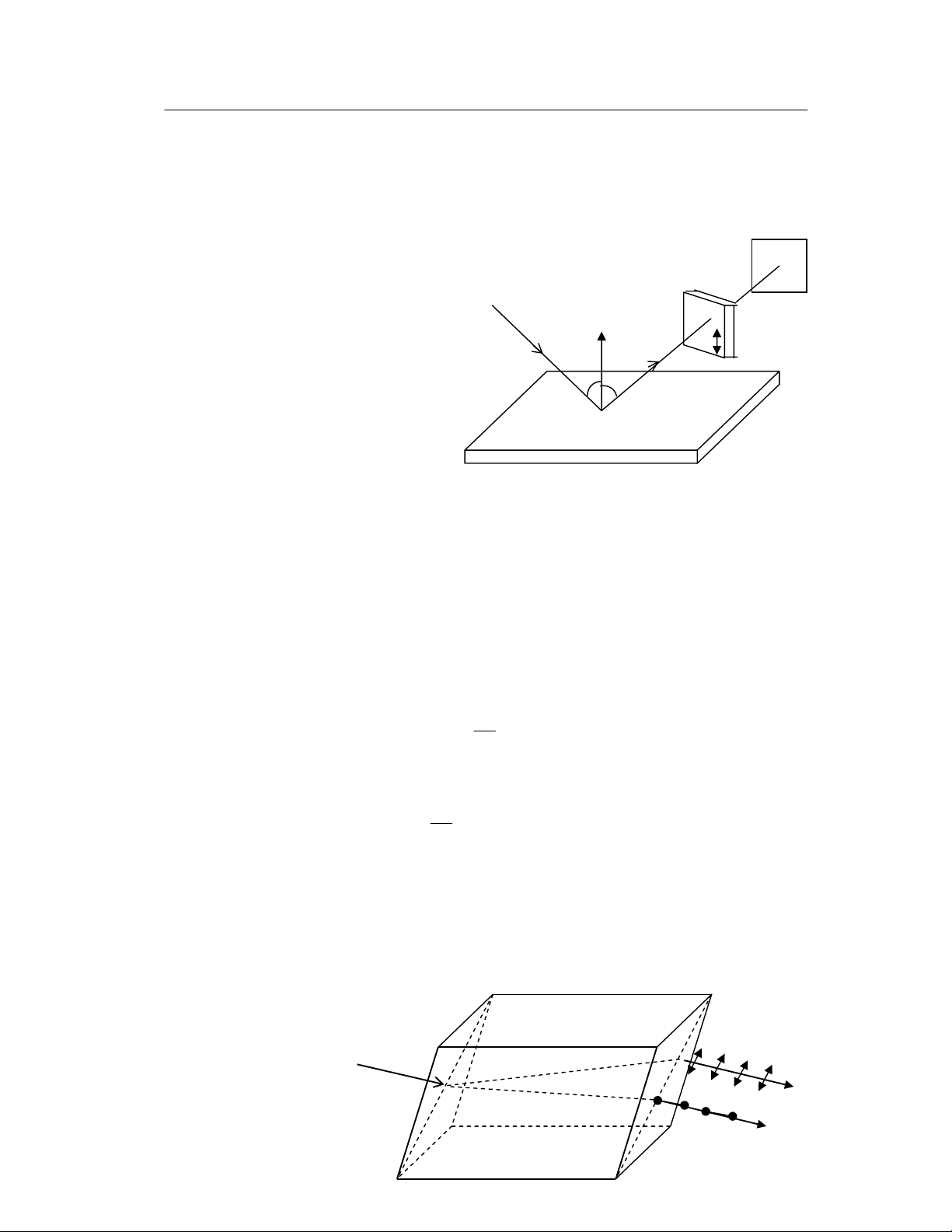
Xét tia sáng SI là ánh sáng
tự nhiên đến đập vào gương phẳng
tại I và cho tia phản xạ IS’. Vấn đề
đặt ra là tia phản xạ này là ánh
sáng tự nhiên hay ánh sáng phân
cực? và nếu là ánh sáng phân cực
thì ánh sáng phân cực hoàn toàn
hay không hoàn toàn
Để trả lời câu hỏi này ta đặt
vuông góc trên đường đi của tia
sáng phản xạ một máy phân cực
phẳng P, rồi quay máy này xung quanh tia sáng. Thí nghiệm cho thấy cường
độ sáng tại S’ lớn nhất khi phương phân cực ∆ vuông góc với mặt phẳng tới
và cực tiểu khi phương phân cực ∆ song song với mặt phẳng tới. Điều đó
chứng tỏ ánh sáng phản xạ của ánh sáng tự nhiên trên gương không phải là
ánh sáng tự nhiên mà là ánh sáng phân cực một phần.
Bây giờ cố định Nicôn và thay đổi góc tới và tiến hành lại thí nghiệm
người ta thấy rằng cường độ sáng tại S’ lớn nhất khi góc tới i thoả mãn điều
kiện: tgi = tgiB =
1
2
n
n = n21
và iB được gọi là góc Briwster. Còn công thức:
tgiB =
1
2
n
n (VII-2).
gọi là điều kiện Briwster.
7.2.2. HIỆN TƯỢNG LƯỠNG CHIẾT
Năm 1670 người ta phát hiện ra hiện tượng một dòng chữ đặt dưới viên
đá Băng lan (CaCO3) thì tách thành 2 dòng. Điều này chứng tỏ tinh thể đá
Băng lan có hai
chiết suất khác
nhau đối với một
tia sáng truyền
qua nó. Người ta
gọi đó là hiện
H. VII-5
I0
IE
I
S D’
C’
B’
A’
D
B
A
C
n
r
Hình VII-4
S
’
N
i’
i
S
Giâo trình Vật lý 2 Ths. Trương Thành
74
tượng lưỡng chiết. Các nghiên cứu tiếp theo chứng tỏ rằng hiện tượng lưỡng
chiết xẩy ra đối với các môi trường bất đẳng hướng như đá Bănglan (một
dạng của tinh thể CaCO3).
Để hiểu rõ hơn hiện tượng này ta xét cấu trúc của tinh thể đá băng lan.
Tinh thể Băng lan là một khối hình hộp xiên (dạng quả trám) có 6 mặt, các
cạnh đều bằng nhau, sáu mặt là các hình thoi bằng nhau. Góc lớn nhất của
hình thoi là 1010 52’ góc bé là 7808’. Như vậy tinh thể này có trục đối xứng
bậc 3 là AA’ (nghĩa là khi quay tinh thể quanh trục AA’ một góc 2π/3 thì
tinh thể lại trùng với chính nó ban đầu (dĩ nhiên ta sẽ gọi trục đối xứng bậc
n nếu phải quay một góc 2π/n . . .). Mọi đường thẳng song song với AA’ đều
là trục đối xứng bậc 3.
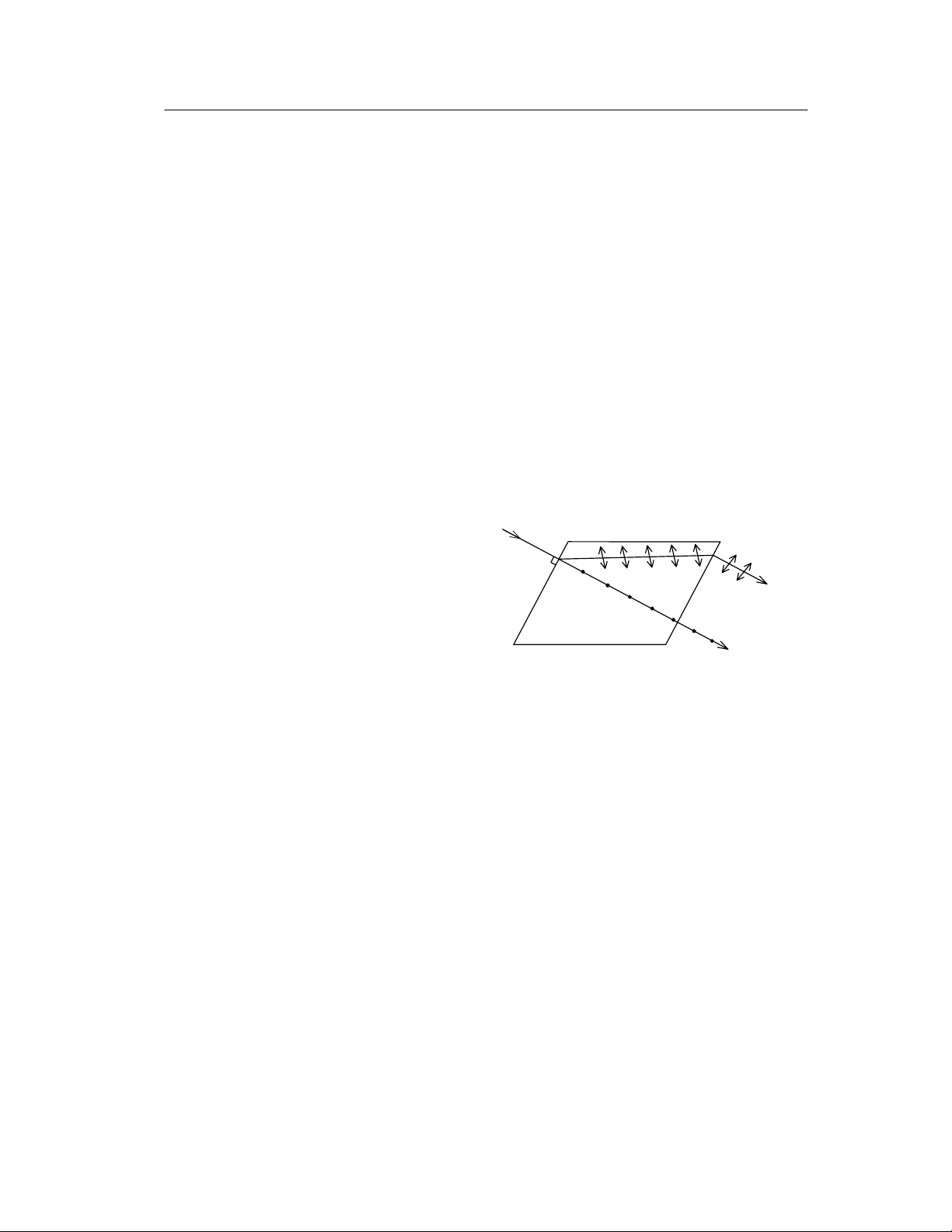
Tia sáng SI chiếu vào tinh thể này bị tách thành hai tia và sau khi ra
khỏi tinh thể lại song song với nhau. Một trong hai tia tuân theo định luật
khúc xạ gọi là tia thường I0 còn tia kia không tuân theo định luật khúc xạ nên
gọi là tia bất thường IE (hình vẽ VII-6). Thí nghiệm cho thấy cả hai tia này
đều phân cực hoàn toàn.
Ngoài ra hình hình vẽ cũng
cho ta thấy tia bất thường bị lệch
ngay cả khi tia tới chiếu vuông góc
với mặt bên của tinh thể.
Người ta cũng tính được rằng
chiết suất của tia thường không phụ
thuộc vào phương truyền và có giá
trị n0 = 1,658. Chiết suất của đá băng
lan đối với tia bất thường thì thay
đổi từ n0 đến nE = 1,486.
S
C A’
I0
IE
A C’
Hình VII-6
Giâo trình Vật lý 2 Ths. Trương Thành
75
7.3. GIẢI THÍCH HIỆN
TƯỢNG LƯỠNG CHIẾT
Trong mục này chúng ta sẽ giải thích hiện tượng lưỡng chiết mà cơ sở
của nó là giả thuyết của Huygens
7.3.1. GỈA THUYẾT CỦA HUYGENS
Để giải thích hiện tượng lưỡng chiết Huggens đã đưa ra giả thuyết sau:
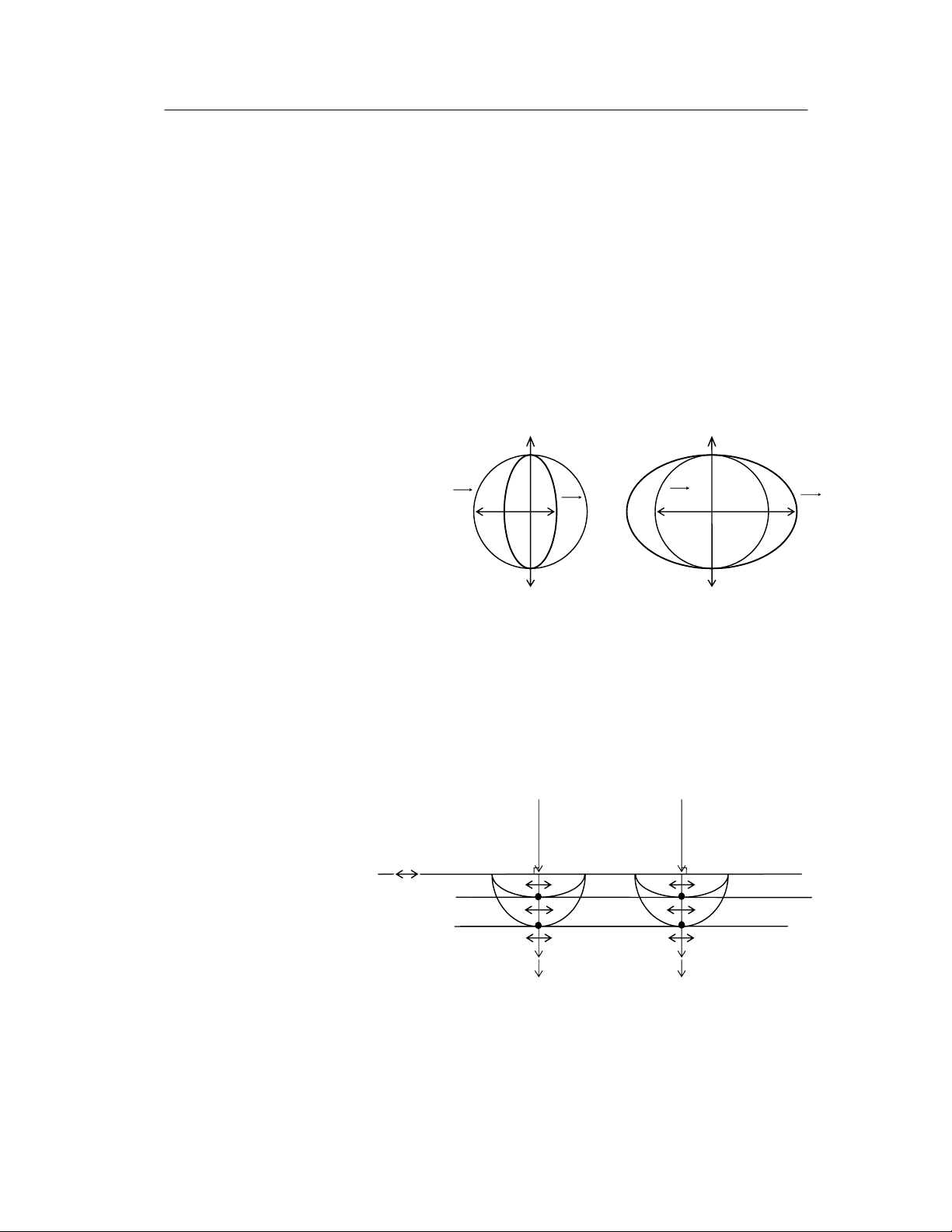
“Trong tinh thể đơn trục tia thường có vận tốc như nhau theo mọi
phương và bằng v0 như vậy mặt đầu sóng của tia thường luôn luôn là mặt
cầu. Còn vận tốc của tia bất thường vE thì phụ thuộc vào phương truyền. Nếu
tia thường đi theo hướng quang trục thì vận tốc truyền bằng vận tốc tia
thường (vE = v0) còn đi theo các hướng khác thì bé hơn (hoặc lớn hơn) nên
mặt đầu sóng là một mặt
Elípsoit tròn xoay’’. Người ta
quy ước:
- Nếu v0 ≥ v
E thì tinh
thể gọi là tinh thể dương.
- Nếu v0 ≤ v
E thì tinh
thể gọi là tinh thể âm
(như hình vẽ VII-7).
- Tia thường kí hiệu
bằng một mũi tên trên
đó có các dấu chấm,
Tia bất thường kí hiệu
bằng một mũi tên trên đó có các gạch ngang mũi tên (xem hình vễ
phía dưới).
7.3.2. GIẢI THÍCH HIỆN TƯỢNG LƯỠNG CHIẾT
Để giải thích
hiện tượng lưỡng
chiết ta dùng giả
thuyết của Huygens
và xét các trường hợp
cụ thể như sau.
7.3.2.1. Tinh thể
dương (v0 > vE), ánh
sáng tới là chùm
song song vuông góc
với mặt phẳng tới
0
v0
v
E
vE
v
(Tinh thể dương) (Tinh thể âm)
(
sau 1
g
iâ
y)
H. VII-7
M∆
E
0
IE
I0
A
IE
I0 0’
E’
N
B
Hình VII-8