MUÏC LUÏC
Trang
Chöông I. HAØM SOÁ LÖÔÏNG GIAÙC VAØ PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
Baøi 1. Caùc haøm soá löôïng giaùc -------------------------------------------------------- 1
Baøi 2. Phöông trình löôïng giaùc cô baûn ---------------------------------------------- 13
Baøi 3. Moät soá phöông trình löôïng giaùc ñôn giaûn ----------------------------------- 22
Baøi taäp oân taäp chöông I --------------------------------------------------------- 35
Chöông II. TOÅ HÔÏP VAØ XAÙC SUAÁT
A- Toå hôïp
Baøi 1. Hai quy taéc ñeám cô baûn ------------------------------------------------------ 39
Baøi 2. Toå hôïp – hoaùn vò – chænh hôïp ----------------------------------------------- 47
Baøi 3. Nhò thöùc NewTon ------------------------------------------------------------ 63
B- Xaùc suaát
Baøi 4. Bieán coá vaø xaùc suaát cuûa bieán coá --------------------------------------------- 73
Baøi 5. Caùc quy taéc tính xaùc suaát ---------------------------------------------------- 83
Baøi 6. Bieán ngaãu nhieân rôøi raïc ------------------------------------------------------ 90
Baøi taäp oân taäp chöông II --------------------------------------------------------- 97
Chöông III. DAÕY SOÁ – CAÁP SOÁ COÄNG – CAÁP SOÁ NHAÂN
Baøi 1. Phöông phaùp quy naïp toaùn hoïc--------------------------------------------- 102
Baøi 2. Daõy soá ---------------------------------------------------------------------- 109
Baøi 3. Caáp soá coäng ---------------------------------------------------------------- 121
Baøi 4. Caáp soá nhaân ---------------------------------------------------------------- 133
Baøi taäp oân taäp chöông III ------------------------------------------------------ 144
Chöông IV. GIÔÙI HAÏN
Baøi 1. Giôùi haïn cuûa daõy soá -------------------------------------------------------- 149
Baøi 2. Giôùi haïn cuûa haøm soá – haøm soá lieân tuïc ---------------------------------- 166
Baøi taäp oân taäp chöông IV ------------------------------------------------------- 184
Chöông V. ÑAÏO HAØM
Baøi 1. Khaùi nieäm Ñaïo Haøm-------------------------------------------------------- 188
Baøi 2. Ñaïo haøm soá hôïp – ñaïo haøm caáp cao – vi phaân --------------------------- 198
Baøi taäp oân taäp chöông V ------------------------------------------------------ 207.
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Để mua bộ tài liệu FILE WORD vui lòng liên hệ
0168 203 6477
1
Chöông I HAØM SOÁ LUÔÏNG GIAÙC VAØ PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
Baøi 1 CAÙC HAØM SOÁ LÖÔÏNG GIAÙC.
A.TOÙM TAÉT LÍ THUYEÁT
1) Haøm soá y = sinx:
Taäp xaùc ñònh D = .
y = sinx laø haøm soá leû do:
x D thì x D vaø sin( x) = sinx.
Haøm soá tuaàn hoaøn vôùi chu kì
2 , töùc laø sin(x + 2 ) = sinx, x.
Haøm soá ñoàng bieán treân moãi khoaûng




k2 , k2 , k vaø nghòch
22




3
bieán treân moãi khoaûng k2 , k2 , k .
22
Taäp giaù trò cuûa haøm soá laø: [-1; 1].
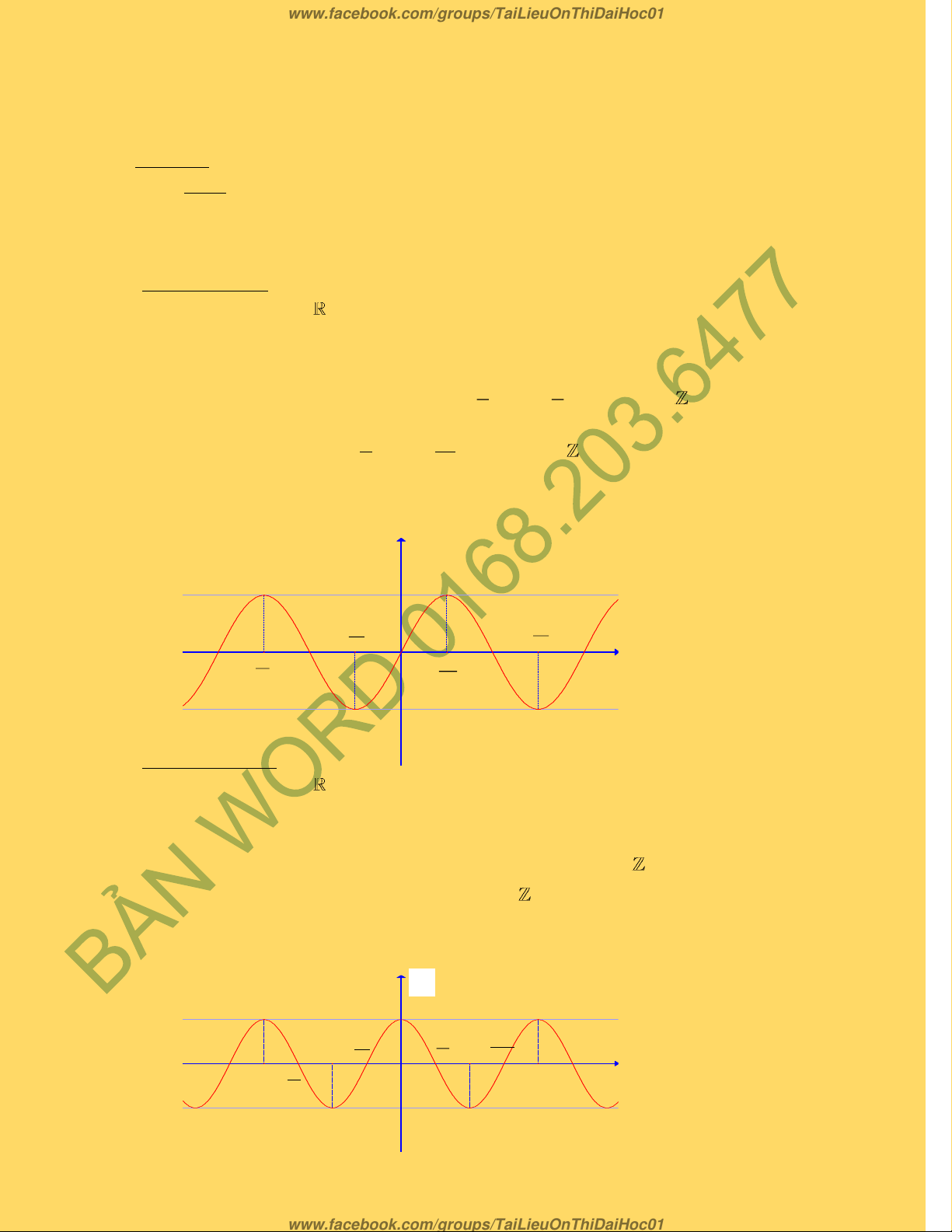
Ñoà thò cuûa haøm soá sinx nhö (hình 1) sau:
2) Haøm soá y = cos x:
Taäp xaùc ñònh D = .
y = cosx laø haøm soá chaün do:
x D thì x D vaø cos( x) = cosx.
Haøm soá tuaàn hoaøn vôùi chu kì
2 , töùc laø cos(x + 2 ) = cosx, x D.
Haøm soá ñoàng bieán treân moãi khoaûng
 k2 , k2 , k vaø nghòch
bieán treân moãi khoaûng k2 , k2 , k .
Taäp giaù trò cuûa haøm soá laø: [-1; 1].
Ñoà thò cuûa haøm soá cosx nhö (hình 2) sau:
-1
1
x
y
-1
1
x
f(x)
Hình 2
y
y =sin x
2
3
2
3
2
2

2
2
3
2
3
2
2

2

y = cos x
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Để mua bộ tài liệu FILE WORD vui lòng liên hệ
0168 203 6477
2
3) Haøm soá y = tan x:
Taäp xaùc ñònh D =



\ k : k .
2
y = tanx laø haøm soá leû do:
x D thì x D vaø tan ( x) = tanx.
Haøm soá tuaàn hoaøn vôùi chu kì
, töùc laø tan(x + ) = tanx, x D.
Haøm soá ñoàng bieán treân moãi khoaûng




k , k , k .
22
Ñoà thò nhaän caùc ñöôøng thaúng
x k , k
2
laøm caùc ñöôøng tieäm caän cuûa
ñoà thò haøm soá.
Taäp giaù trò cuûa haøm soá laø: .
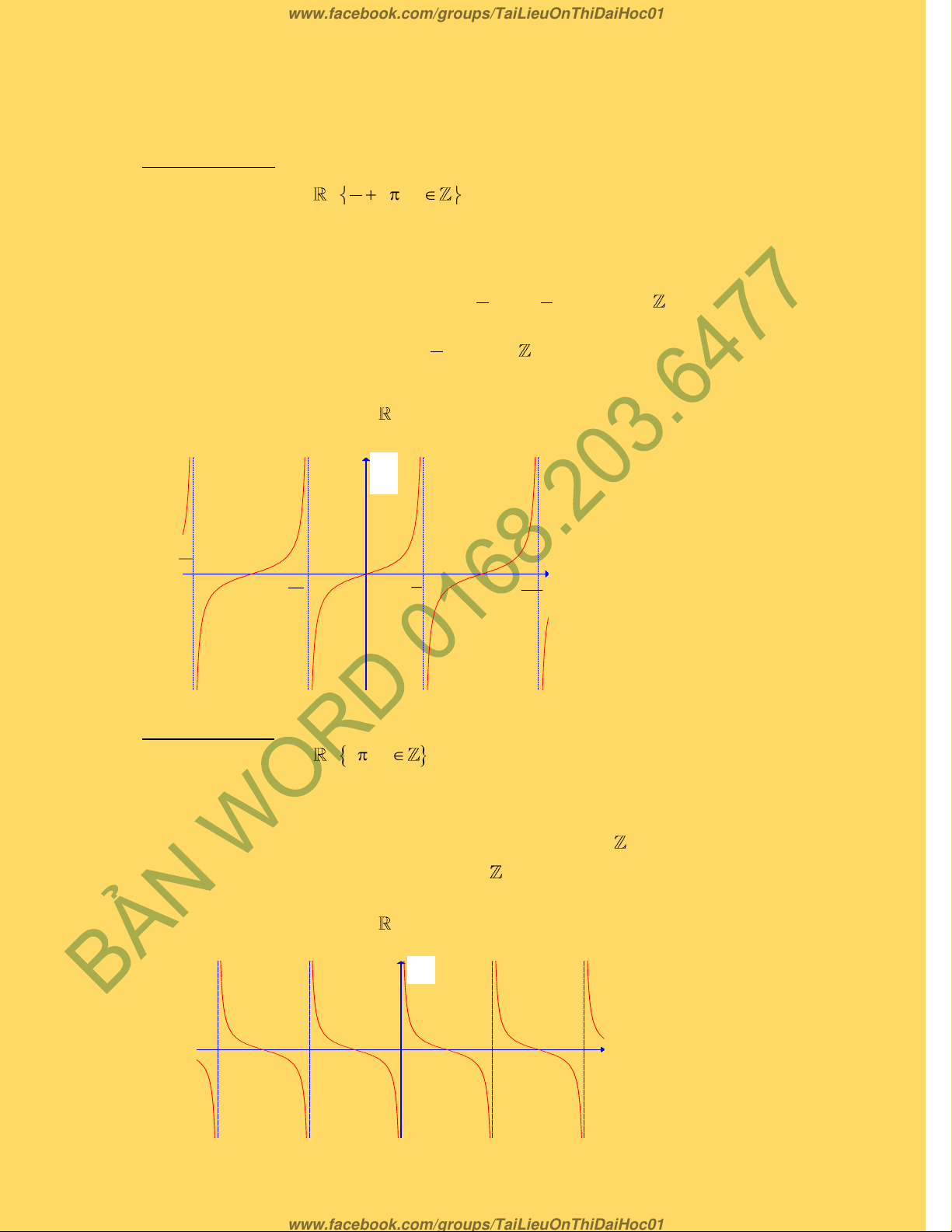
Ñoà thò cuûa haøm soá tanx nhö (hình 3)sau:
4) Haøm soá y = cot x:
Taäp xaùc ñònh D =
\ k : k .
y = cot x laø haøm soá leû do:
x D thì x D vaø cot( x) cotx.
Haøm soá tuaàn hoaøn vôùi chu kì
, töùc laø cot(x + ) = cotx, x.
Haøm soá nghòch bieán treân moãi khoaûng
k , k , k .
Ñoà thò nhaän caùc ñöôøng thaúng
x k , k
laøm caùc ñöôøng tieäm caän cuûa ñoà thò
haøm soá.
Taäp giaù trò cuûa haøm soá laø: .
Ñoà thò cuûa haøm soá cot x nhö (hình 4) sau:
x
f(x)
Hình 3
y
x
f(x)
Hình 4
y
2
3
2
3
2
2


y = tan x
y = cot x
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Để mua bộ tài liệu FILE WORD vui lòng liên hệ
0168 203 6477
3
B. PHÖÔNG PHAÙP GIAÛI TOAÙN
Vaán ñeà1:
Tìm taäp giaù trò, taäp xaùc ñònh cuûa caùc haøm soá löôïng giaùc.
Phöông phaùp:
Để tìm miền xaùc ñònh của hàm số y = f(x) ta dựa vào điều kiện xác định của hàm
số:
1
* Neáu y = thì haøm soá ñöôïc xaùc ñònh khi A(x) 0.
A(x)
* Neáu y = A(x) thì haøm soá ñöôïc xaùc ñònh khi A(x) 0.
1
* Neáu y = thì haøm soá ñöôïc xaùc ñònh khi A(x)> 0.
A(x)
Ñeå tìm mieàn giaù trò cuûa haøm soá löôïng giaùc chuùng ta thöôøng duøng caùc baát ñaúng
thöùc löôïng giaùc cô baûn sau:
1 sinx 1, x.
1 cosx 1, x.
ñeå tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá.
Ví duï1: Tìm taäp xaùc ñònh cuûa caùc haøm soá sau:


22
1 x 1 cosx
a) y= 2 sin x b) y = .
1 cosx
3 cosx
Giaûi:
a) Töø ñieàu kieän xaùc ñònh cuûa haøm soá laø:
2
3 cosx 0 (*).
2 sin x 0


Ta coù: (*) luoân ñuùng vôùi moïi
x.
Vì
1 cosx 1 neân 3- cosx > 0, x.
22
Do -1 sinx 1, x neân 0 sin x 1. Suy ra: 2-sin x>0
Vaäy mieàn xaùc ñònh cuûa haøm soá laø D=.
b) Haøm soá
1 cosx
y = 1 cosx
ñöôïc xaùc ñònh khi:
1 cosx 01 cosx 0 cosx 1 x k2 , k .
1 cosx
1 cosx 0
Vaäy D = \ k2 : k .


Ví duï 2: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa caùc haøm soá sau:
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
Để mua bộ tài liệu FILE WORD vui lòng liên hệ
0168 203 6477
4



3
a) y = 2 sin x+ 3 b) y = 1 cos(x ) 2.
4
Giaûi:
a)



y = 2 sin x+ 3 coù mieàn xaùc ñònh D= .
4
Vì 1 sin x+ 1, x neân 2 2sin x+ 2.
44

Do ñoù: 2 3 y 2sin x+ 3 3 2.
4
Vaäy giaù trò lôùn nhaát cuûa haøm soá laø y = 3 2 khi sin x+ 1.
4
Giaù trò nhoû nhaát cuûa haøm soá laø y = 3 2 khi sin x+ 1.
4










b) Haøm soá

3
y = 1 cos(x ) 2 .
33
33
3
Vì 1 cos(x ) 1, x neân 1 cos(x ) 0,
neân haøm soá coù mieàn xaùc ñònh laø D= . Hôn nöõa:
0 1 cos(x ) 2 neân 0 1 cos(x ) 2.
Do ñoù: 2 y 1 cos(x ) 2 2 2.
Vaäy giaù trò lôùn nhaát cuûa haøm soá laø y =
3
3
2 2 khi cos(x ) 1.
Giaù trò nhoû nhaát cuûa haøm soá laø y = 2 khi cos(x ) 1.

Vaán ñeà 2:
Veõ ñoà thò caùc haøm soá löôïng giaùc.
Phöông phaùp:
1) Veõ ñoà thò haøm soá löôïng giaùc: y = sin(ax), a > 0: Ta chæ caàn xeùt söï bieán thieân cuûa
noù treân moät ñoaïn coù ñoä daøi baèng moät chu kì
2
Ta
, chaúng haïn laø ñoaïn



2
0; .
a
Ta laäp baûng giaù trò vaø veõ ñoà thò.
Töông töï cho caùc haøm soá y = cos(ax); y = tan(ax); y = cot(ax).
2) Veõ ñoà thò haøm soá löôïng giaùc daïng: y = sin(ax + b) + c: Ta laøm theo caùc böôùc
sau:
Veõ ñoà thò haøm soá daïng y = sin(ax) ( laøm nhö 1) treân).
Ñoà thò cuûa haøm soá y = sin(ax + b) coù ñöôïc töø ñoà thò (C) cuûa haøm soá
y = sin(ax) baèng caùch tònh tieán (C) sang traùi |b| ñôn vò neáu neáu b > 0 vaø tònh
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01
www.facebook.com/groups/TaiLieuOnThiDaiHoc01