SÔÛ GIAÙO DUÏC VAØ ÑAØO TAÏO KYØ THI TUYEÅN SINH VAØO LÔÙP 10
BÌNH THUẬN TRƯỜNG THPT CHUYÊN TRẦN HƯNG ĐẠO
Năm học : 2011 – 2012
ĐỀ CHÍNH THỨC Môn: Toán (hệ số 1)
(Đề thi này có 01 trang) Thời gian: 120 phút (không kể thời gian phát đề)
ĐỀ
Bài 1: ( 2 điểm)
Cho hai biểu thức:
2
( a ) 4
vaøB =
a b b a b ab
Aab a b
( với a > 0, b > 0 và a
b)
1/ Rút gọn A và B
2/ Tính tích A.B với
2 5
a,
5
b
Bài 2: ( 2 điểm)
Giải các phương trình và hệ phương trình sau:
1/ x4 – 6x3 + 27x – 22 = 0
2/
2 3
4
2 3
1 2
9
2 3
x y x y
x y x y
Bài 3: ( 2 điểm)
Một xe ô tô đi từ A đến B cách nhau 180km. Sau khi đi được 2 giờ, ô tô dừng
lại để đổ xăng và nghỉ ngơi mất 15 phút rồi tiếp tục đi với vận tốc tăng thêm 20 km/h
và đến B đúng giờ đã định. Tìm vận tốc ban đầu của xe ô tô.
Bài 4: (3 điểm)
Cho tam giác đều ABC cạnh a, nội tiếp trong đường tròn (O).
1/ Tính theo a phần diện tích hình tròn (O) nằm ngoài tam giác ABC.
2/ Trên cạnh BC lấy điểm M tùy ý (M khác B, C); từ M kẻ MP, MQ lần lượt
vuông góc với AB, AC tại P, Q. Chứng minh:
a/ Tứ giác APMQ nội tiếp.
b/ Khi điểm M di động trên cạnh BC thì tổng MP + MQ không đổi.
Bài 5: (1 điểm)
Cho tam giác ABC có
A
= 600 . Chứng minh BC2 = AB2 + AC2 – AB.AC
-------------- HẾT -------------
ĐÁP ÁN KỲ THI TS VÀO 10 THĐ( hệ số 1) - Năm học 2011 – 2012
LỜI GIẢI TÓM TẮT
ĐIỂM
Bài 1: (2đ)
1/ (1,0đ)
( )ab a b
A a b
ab
2
2 ( )a b ab a b
B a b
a b a b
0,5
0,5
2/ (1,0 đ)
A.B =
( )( ) 5
a b a b a b
1,0
Bài 2: (2đ)
1/ (1,0 đ)
4 3 4 3 2 2
6 27 22 0 6 9 9 27 22 0
x x x x x x x x
2 2 2
( 3 ) 9( 3 ) 22 0
x x x x
Đặt t = x2 -3x , ta có pt : t2 – 9t – 22 = 0
t = -2 ; t = 11
t = -2 : x2 – 3x + 2 = 0
x =1 ; x = 2
t = 11 : x2 – 3x – 11 =0
x =
3 53
2
Kết luận phương trình có 4 nghiệm
0,25
0,25
0,25
0,25
2/
(1,0 đ)
Điều kiện 2x - 3y
0 và x + y
0
Đặt
1 1
;
2 3
u v
x y x y
Ta có hệ :
2 3 4 5
2 9 2
u v u
u v v
Khi đó :
1
1
52 3
2 3
5
1
1
2
2
x y
x y hay
x y
x y
Tính được
17
50
4
25
x
y
(thỏa điều kiện)
0,25
0,25
0,25
0,25
Bài 3: (2đ)
Gọi x(km/h) là vận tốc ban đầu của xe ô tô (x > 0)
Thì vận tốc lúc sau là x + 20 (km/h)
Quãng đường đi được sau 2 giờ là: 2x (km)
Quãng đường đi sau khi nghỉ ngơi là: 180 – 2x (km)
Viết được phương trình:
180 1 180 2
2
4 20
x
x x
Hay x2 + 180x – 14400 = 0
Tìm được x = 60; x = -240 (loại)
Vậy vận tốc ban dầu của xe là 60km/h
0,25
0,25
0,25
0,5
0,25
0,25
0,25
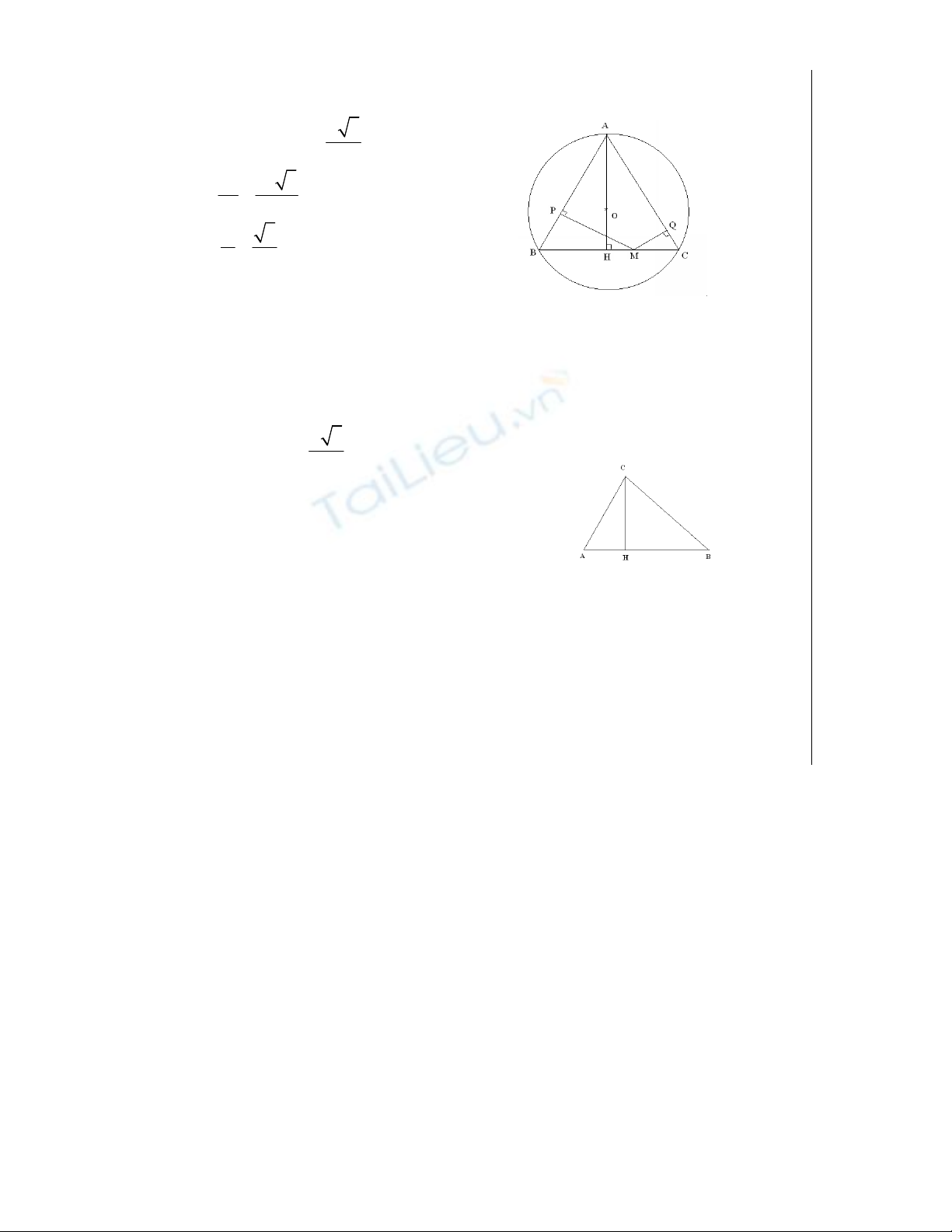
Bài 4: (3đ)
1/ Gọi S là phần diện tích (O) nằm ngoài tam giác ABC:
Ta có: Bán kính (O) : R =
3
3
a
S = 2 2
3
.
3 4
a a
= a2(
3
3 4
)
2/
a/ Các điểm P và Q nhìn đoạn AM dưới một góc vuông
nên thuộc đường tròn đường kính AM
do đó tứ giác APMQ nội tiếp
b/ Vẽ AH là đường cao tam giác ABC.
S
ABC = S
ABM + S
ACM
hay: BC.AH = AB.MP + AC.MQ = BC(MP + MQ) ( do ABC đều)
hay AH = MP + MQ =
3
2
a không đổi.
Bài 5: (1đ)
Gọi CH là đường cao hạ từ C và
A
= 600 nên AC = 2AH
AB2 + AC2 – AB.AC = (AH+HB)2 + AH2 +HC2 – (AH+HB).2AH
= HB2 + HC2 = BC2.
0.25
0.5
0.25
0.5
0.5
0.5
0.5
0.25
0.5
0.25