Tương lai không phải thuộc về những người thông minh nhất mà thuộc về những người cần cù và siêng năng nhất!
LÍ THUYẾT CHƯƠNG SÓNG ÁNH SÁNG
I. TÓM TẮT CÔNG THỨC GIAO THOA ÁNH SÁNG
Giao thoa với khe Young (Y-âng hay I-âng)
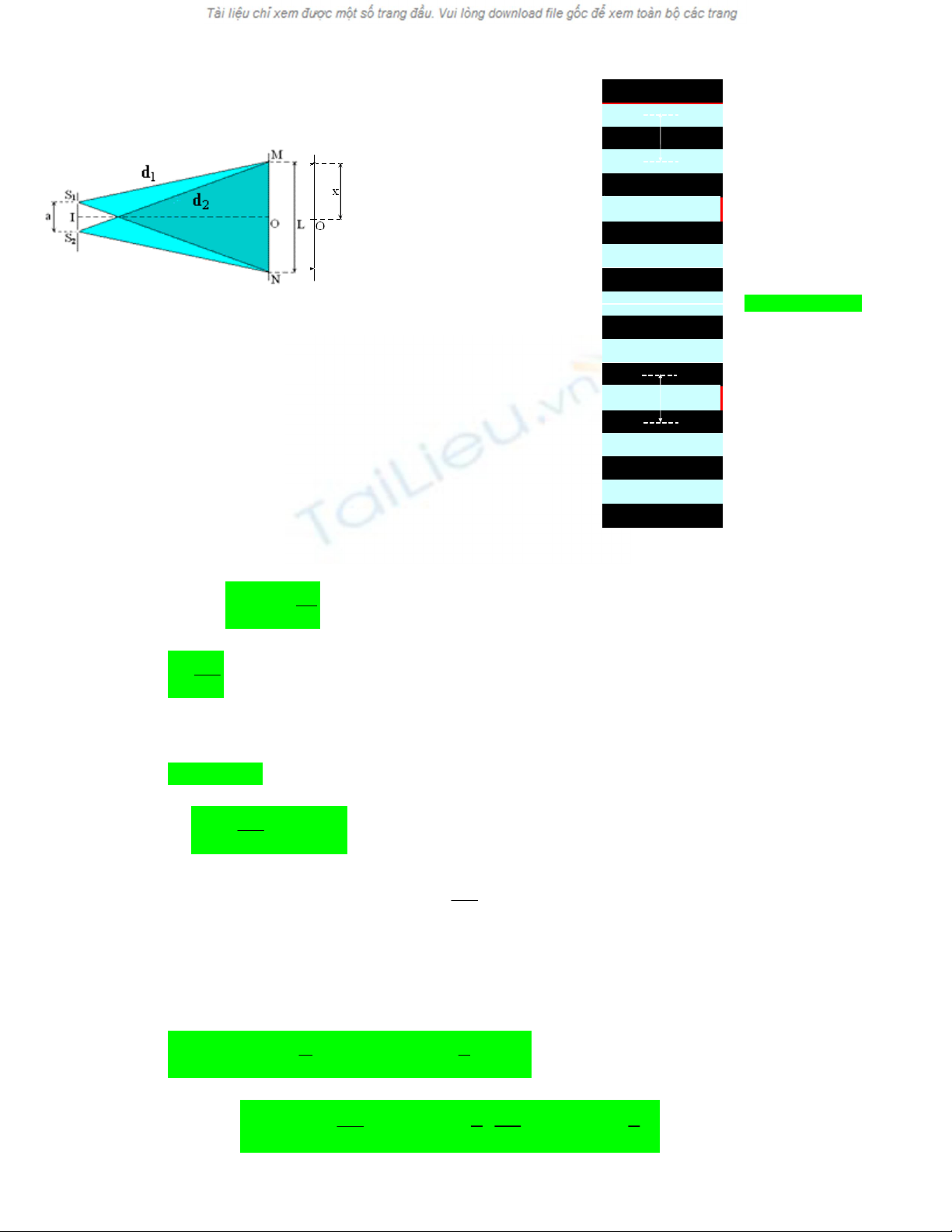
Thí nghiệm giao thoa ánh sáng của Young
S1, S2 là hai khe sáng; O là vị trí vân sáng
trung tâm
a (m): khoảng cách giữa hai khe sáng;
D (m): khoảng cách từ hai khe sáng đến màn
λ (m): bước sóng ánh sáng;
L (m): bề rộng vùng giao thoa,
Hình ảnh vân giao thoa
1. Hiệu đường đi từ S1, S2 đến điểm A trên màn
Xét D >> a, x thì: d2 – d1 = D
ax (1)
2. Khoảng vân i Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp gọi là khoảng vân
D
ia
(2)
3. Vị trí vân sáng và vân tối
a. Vị trí vân sáng
Tại A có vân sáng khi hai sóng cùng pha, hiệu đường đi bằng số nguyên lần bước sóng:
d2 – d1 = k
(3)
Điều kiện trên còn được gọi là điều kiện cực đại giao thoa.
xs = k a
D
hay xs=ki (với k
Z). (4)
Khi k = 0 thì x = 0: ứng với vân sáng trung tâm hay vân sáng chính giữa.
Khi k = 1: ứng với vân sáng bậc (thứ) 1. x =
a
D
Khi k = 2: ứng với vân sáng bậc (thứ) 2. ......
Khi k = n: ứng với vân sáng bậc (thứ) n (n là số nguyên dương)
b. Vị trí vân tối
Tại M có vân tối khi hai sóng từ hai nguồn đến M ngược pha nhau. Điều kiện này thỏa mãn khi hiệu đường
đi từ hai nguồn đến M bằng số lẻ nửa bước sóng (số bán nguyên bước sóng)
d
2 – d1 = (2k + 1) 2
hay d2 – d1 = (k+ 1
2)
(5)
Điều kiện trên còn được gọi là điều kiện cực tiểu giao thoa.
Từ (1) và (5) ta có: t
x = (2k +1) a
D
2
, hay 1D
xk
2a
, hay 1
xk i
2
(6)
vuøng giao thoa
Tối thứ1
,
k= 0
Tối thứ3
,
k=2
Tối thứ4
,
k=3
Tối thứ5
,
k=4
Tối thứ2
,
k= 1
Tối thứ2
,
k=1
Tối thứ3
,
k= 2
Tốithứ4
,
k= 3
i
i
Vân sán
g
TT
,
k= 0
Sán
g
thứ 1
,
k= 1
,
b
ậ
c 1
Sán
g
thứ2
,
k=-2
,
b
ậ
c 2
Sán
g
thứ3
,
k=-3
,
b
ậ
c 3
Sán
g
thứ 4
,
k=-4
,
b
ậ
c
Sán
g
thứ2
,
k= 2
,
b
ậ
c 2
Sán
g
thứ 1
,
k=-1
,
b
ậ
c 1
Sán
g
thứ3
,
k= 3
,
b
ậ
c 3
Sán
g
thứ 4
,
k= 4
,
b
ậ
c 4
Tối thứ1
,
k=0
Tốithứ5
,
k= 4

Tương lai không phải thuộc về những người thông minh nhất mà thuộc về những người cần cù và siêng năng nhất!
Tổng quát :vị trí vân tối xác định bởi công thức: ikxt)
2
1
( ;k=0 vân tối thứ 1;k=1 vân tối thứ
2.........
II.MỘT SỐ DẠNG TOÁN
1. Gọi L là khoảng cách giữa n vân sáng liên tiếp hoặc khoảng cách giữa n vân tối liên tiếp.
L=(n 1)i, i = L
n1 (1)
* Xác định khoảng vân i trong khoảng có bề rộng L. Biết trong khoảng L có n vân sáng.
+ Nếu 2 đầu là hai vân sáng thì: 1
L
in
=-
+ Nếu 2 đầu là hai vân tối thì:
L
in
=
+ Nếu một đầu là vân sáng còn một đầu là vân tối thì: 0,5
L
in
=-
2. Xác định vị trí một điểm M bất kì trên trường giao thoa cách vân trung tâm một khoảng xM có vân sáng hay
vân tối
+ Lập tỉ số: M
xn
i (2)
Nếu n nguyên, hay n Z, thì tại M có vân sáng bậc k=n.
Nếu n bán nguyên hay n=k+0,5 với kZ, thì tại M có vân tối thứ (k +1).
3. Xác định số vân sáng quan sát được trên màn
+ Gọi L là bề rộng của trường giao thoa trên màn.
-Lập tỉ số: i
L
2
-Số vân sáng : 1
2
2
i
L
NS -Số vân tối:
5,0
2
2i
L
NT
Với
là lấy phần nguyên của biểu thức bên trong dấu ngoặc vuông.
Ví dụ:
27,2 ;
22,2
4. Giao thoa với khe Young trong môi trường có chiết suất là n
Gọi
là bước sóng ánh sáng trong chân không hoặc không khí =c/f.
Gọi ' là bước sóng ánh sáng trong môi trường có chiết suất n: ’=v/f.
nc
v1
,
hay n
, (6)
a. Vị trí vân sáng: xs’ = k'D
a
=kD x
n.a n
(7)
b.Vị trí vân tối: xt’ =(2k +1) 'D
2a
= (2k +1) t
x
D
2na n
(8)
c. Khoảng vân: i’= 'D
a
= Di
an n
(9)
5. Giao thoa ánh sáng với nhiều bức xạ đơn sắc
Tìm vị trí vân sáng của các bức xạ đơn sắc trùng nhau, các vân sáng trùng nhau có màu giống màu vân trung tâm
x =
a
D
k1
1
= a
D
k2
2
= a
D
k3
3
= …= a
D
kn
n
. (10)
k
1i1=k2i2=k3i3=k4i4=....=knin. (11)
k
1λ1=k2λ2=k3λ3=k4λ4=....=knλn. (12)
với k1, k2, k3,…, kn Z

Tương lai không phải thuộc về những người thông minh nhất mà thuộc về những người cần cù và siêng năng nhất!
22
12 2
11
i
kk k
i
(13)
Dựa vào phương trình biện luận chọn các giá trị k thích hợp, thông thường đưa tỉ số trên về phân số của hai số nguyên
tối giản, chọn k1 và k2 là bội số của số nguyên đó.
Ví dụ: Thí nghiệm Yuong về giao thoa cho a=1mm, D=2m, hai bức xạ λ1=0,6m và λ2 =0,5m cho vân sáng trùng
nhau. Xác định vị trí trùng nhau.
Ta có k1λ1=k2λ2 2
122
1
5
kkk
6
; ta chọn được k2 là bội của 6 và k1 là bội của 5
Có thể lập bảng như sau:
k1 0 5 10 15 20 25 .....
k2 0 6 12 18 24 30 .....
x 0 6mm 12mm 18mm 24mm 30mm .....
6. Giao thoa ánh sáng với nhiều bức xạ đơn sắc hay ánh sáng trắng
1=0,4.10-6m (tím)
0,75.10-6m=
2 (đỏ)
a. Xác định bề rộng quang phổ bậc k trong giao thoa với ánh sáng trắng
Bề rộng quang phổ là khoảng cách giữa vân sáng màu đỏ ngoài cùng
và vân sáng màu tím của một vùng quang phổ.
xk= xđk-xtk = dt
DD
kk
aa
, xk = k )( td
a
D
, xk = k(iđ it) (14)
với k N*, k là bậc quang phổ.
b. Xác định các bức xạ của ánh sáng trắng cho vân sáng tại x0
Tại x0 có thể là giá trị đại số xác định hoặc là một vị trí chưa xác định cụ thể.
Vị trí vân sáng bất kì x= a
D
k
=x0 kD
ax0
. (15)
với điều kiện
1
2, thông thường
1=0,4.10-6m (tím)
0,75.10-6m=
2 (đỏ)
D
1
0
2
0
ax
k
D
ax , (với k
Z) (16)
Số giá trị kZ chọn được là số bức xạ cho vân sáng tại x0. và thay các giá trị k tìm được vào tính
. đó là các bước
sóng các bức xạ của ánh sáng trắng cho vân sáng tại x0.
c. Các bức xạ của ánh sáng trắng cho vân tối (bị tắt) tại x0:
khi x = (k+ 1
2)D
a
=x0 0
ax
1
(k )D
2
(17)
với điều kiện
1
2
10
ax
1
(k )D
2
2 (18)
00
21
ax ax
1
k
D2D
, (với k
Z) (19)
Số giá trị kZ chọn được là số bức xạ cho vân tối tại x0 (bị tắt tại x0). và thay các giá trị k tìm được vào tính
.
7. Xác định số vân sáng, số vân tối giữa hai điểm M, N
M, N có toạ độ x1, x2 (giả sử x1 < x2)
+ Vân sáng: x1 < ki < x2 (20)
+ Vân tối: x1 < (k+0,5)i < x2 (21)
Số giá trị k Z là số vân sáng (vân tối) cần tìm
Lưu ý: M và N cùng phía với vân trung tâm thì x1 và x2 cùng dấu.
M và N khác phía với vân trung tâm thì x1 và x2 khác dấu.
8. Đặt bản mỏng trước khe Young
Trong thí nghiệm giao thoa ánh sáng với khe Young (I-âng), nếu ta đặt trước khe 1
S một bản thủy tinh có chiều dày e,
chiết suất n. Hệ vân bị lệch một đoạn x0 về phía khe đặt bản mỏng.
1
x


























