Sáng
t oạ
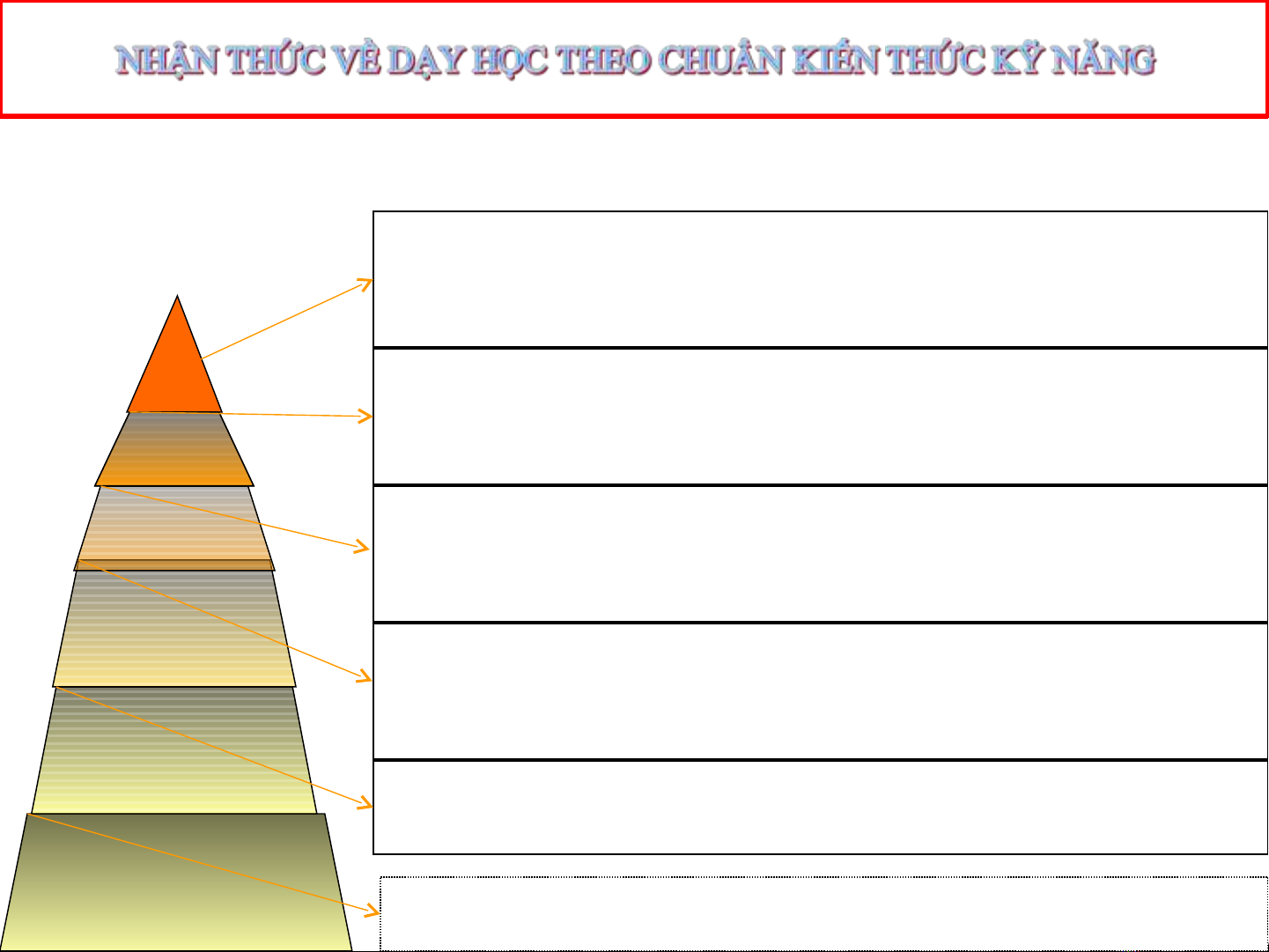
Phân lo i m c đ c n đ t đ c v ki n th c kĩ năngạ ứ ộ ầ ạ ượ ề ế ứ
Nh n bi tậ ế : Là kh năng ghi nh , nh n di n thông tinả ớ ậ ệ
Thông hi uể : là kh năng di n d ch, di n gi i, gi i thích ả ễ ị ễ ả ả
ho c suy di n. (d đoán đ c k t qu và nh h ng)ặ ễ ự ượ ế ả ả ưở
V n d ngậ ụ : Là kh năng s d ng thông tin t m t s ả ử ụ ừ ộ ự
vi c này sang m t s vi c khácệ ộ ự ệ . (S d ng nh ng hi u ử ụ ữ ể
bi t trong hoàn c nh m i)ế ả ớ
Phân tích : Là kh năng nh n bi t chi ti t, phát hi n và ả ậ ế ế ệ
phân bi tệ đ c các b ph n c u thành c a thông tin ượ ộ ậ ấ ủ
hay tình hu ngố
Đánh giá : Là kh năng xác đ nh giá tr c a thông tin: ả ị ị ủ
Bình xét, nh n đ nh, xác đ nh đ c giá tr c a m t t ậ ị ị ượ ị ủ ộ ư
t ng, m t n i dung ki n th c…ưở ộ ộ ế ứ
Sáng t oạ : Là kh năng t ng h p, s p x p, thi t k l i ả ổ ợ ắ ế ế ế ạ
thông tin khai thác, b sung thông tin t các ngu n t ổ ừ ồ ư
li u khác đ sáng l p hình m u m iệ ể ậ ẫ ớ
Đánh
giá
Phân tích
V n d ng ậ ụ
Thông hi u ể
Nh n bi t ậ ế
M T S V N Đ V CHU N KI N TH C K NĂNGỘ Ố Ấ Ề Ề Ẩ Ế Ứ Ỹ
HÌNH H C 12Ọ
*********************************
b) XĐ VTCP c a dủ
V N Đ 1: KHO NG CÁCHẤ Ề Ả
H C SINH Y UỌ Ế
1. Ki n th c: VTPT, VTCPế ứ
2. Kĩ năng: XĐ đ c vecto pháp tuy n c a mp, VTCP c a đ ng th ngượ ế ủ ủ ườ ẳ
VD1: Cho
A(1;2;3)
,
(P) : x y z 1 0
+ + + =
,
x t
d : y t
z 1 t
=
=
= +
a) XĐ VTPT c a (P)ủ
M T S V N Đ V CHU N KI N TH C K NĂNGỘ Ố Ấ Ề Ề Ẩ Ế Ứ Ỹ
HÌNH H C 12Ọ
*********************************
V N Đ 1: KHO NG CÁCHẤ Ề Ả
H C SINH TRUNG BÌNHỌ
1. Ki n th c: Giao đi m c a đ ng th ng v i m t ph ngế ứ ể ủ ườ ẳ ớ ặ ẳ
2. Kĩ năng: Tìm đ c giao đi mượ ể
VD1: Cho
A(1;2;3)
,
(P) : x y z 1 0
+ + + =
,
x t
d : y t
z 1 t
=
=
= +
a) Vi t ptdt quếa A và vuông góc v i (P). ớTìm t a đ giao đi mọ ộ ể
b) Vi t ptmp qua A và vuông góc v i d. Tìm t a đ giao đi mế ớ ọ ộ ể
M T S V N Đ V CHU N KI N TH C K NĂNGỘ Ố Ấ Ề Ề Ẩ Ế Ứ Ỹ
HÌNH H C 12Ọ
*********************************
V N Đ 1: KHO NG CÁCHẤ Ề Ả
H C SINH KHÁỌ
1. Ki n th c: Hình chi u c a m t đi m trên đt, mpế ứ ế ủ ộ ể
2. Kĩ năng: XĐ đ c hình chi u c a m t đi m trên đt, mpượ ế ủ ộ ể
VD1: Cho
A(1;2;3)
,
(P) : x y z 1 0
+ + + =
,
x t
d : y t
z 1 t
=
=
= +
XĐ hình chi u vuông góc c a A trên (P) và dế ủ
M T S V N Đ V CHU N KI N TH C K NĂNGỘ Ố Ấ Ề Ề Ẩ Ế Ứ Ỹ
HÌNH H C 12Ọ
*********************************
V N Đ 1: KHO NG CÁCHẤ Ề Ả
H C SINH GI IỌ Ỏ
1. Ki n tếh c: Kho ng cách liên quan đ n c c trứ ả ế ự ị
2. Kĩ năng: Hi u và v n d ng t t ki n th c v kho ng cách đ gi i toánể ậ ụ ố ế ứ ề ả ể ả
VD1: Cho
A(1;2;3)
,
(P) : x y z 1 0
+ + + =
,
x t
d : y t
z 1 t
=
=
= +
a) Tìm đi m B trên (P) sao cho kho ng cách t A đ n ể ả ừ ế (P) nh nh tỏ ấ
b) Tìm đi m C trên d sao cho kho ng cách t A đ n d nh nh tể ả ừ ế ỏ ấ