CH NG III: PH NG PHÁP T A Đ TRONG M T PH NG (20 ti t)ƯƠ ƯƠ Ọ Ộ Ặ Ẳ ế
§1.PH NG TRÌNH T NG QUÁT C A Đ NG TH NG (2 ti t)ƯƠ Ổ Ủ ƯỜ Ẳ ế
I. M c tiêu:ụ
-Hi u đ c vect pháp tuy n c a đ ng th ng, ph ng trình t ng quát và các d ng đ tể ượ ơ ế ủ ườ ẳ ươ ổ ạ ặ
bi t c a đ ng th ngệ ủ ườ ẳ
-Vi t đ c PTTQ c a đ ng th ng đi qua 1 đi m và có 1 vtpt cho tr c. Bi t xác đ nh vtptế ượ ủ ườ ẳ ể ướ ế ị
c a đ ng th ng khi cho PTTQ c a nóủ ườ ẳ ủ
-Xác đ nh đ c v trí t ng đ i gi a hai đ ng th ng và bi t cách tìm to đ giao đi mị ượ ị ươ ố ữ ườ ẳ ế ạ ộ ể
(n u có) c a hai đ ng th ng khi bi t PTTQ c a chúng.ế ủ ườ ẳ ế ủ
II.Chu n b ph ng ti n d y h c:ẩ ị ươ ệ ạ ọ
a)Th c ti n:ự ễ
b)Ph ng ti n:ươ ệ
c)Ph ng pháp:ươ
III.Ti n trình bài h c và các ho t đ ng:ế ọ ạ ộ
Ho t đ ng 1:ạ ộ Tìm PTTQ c a đ ng th ngủ ườ ẳ
Ho t đ ng c a tròạ ộ ủ Ho t đ ng c a giáo viênạ ộ ủ N i dung c n ghiộ ầ
*
1 2 3
, ,n n n
ur uur uur
0≠r
vàn m trên cácằ
đ ngườ
th ng vuông gócẳ
v i (D) ớ
*HS gi i quy t ?1ả ế
*Hs làm theo yêu c u c aầ ủ
giáo viên
*Có 1 đ ng th ng đi qua Iươ ẳ
và nh n ậ
n
r
làm vtpt
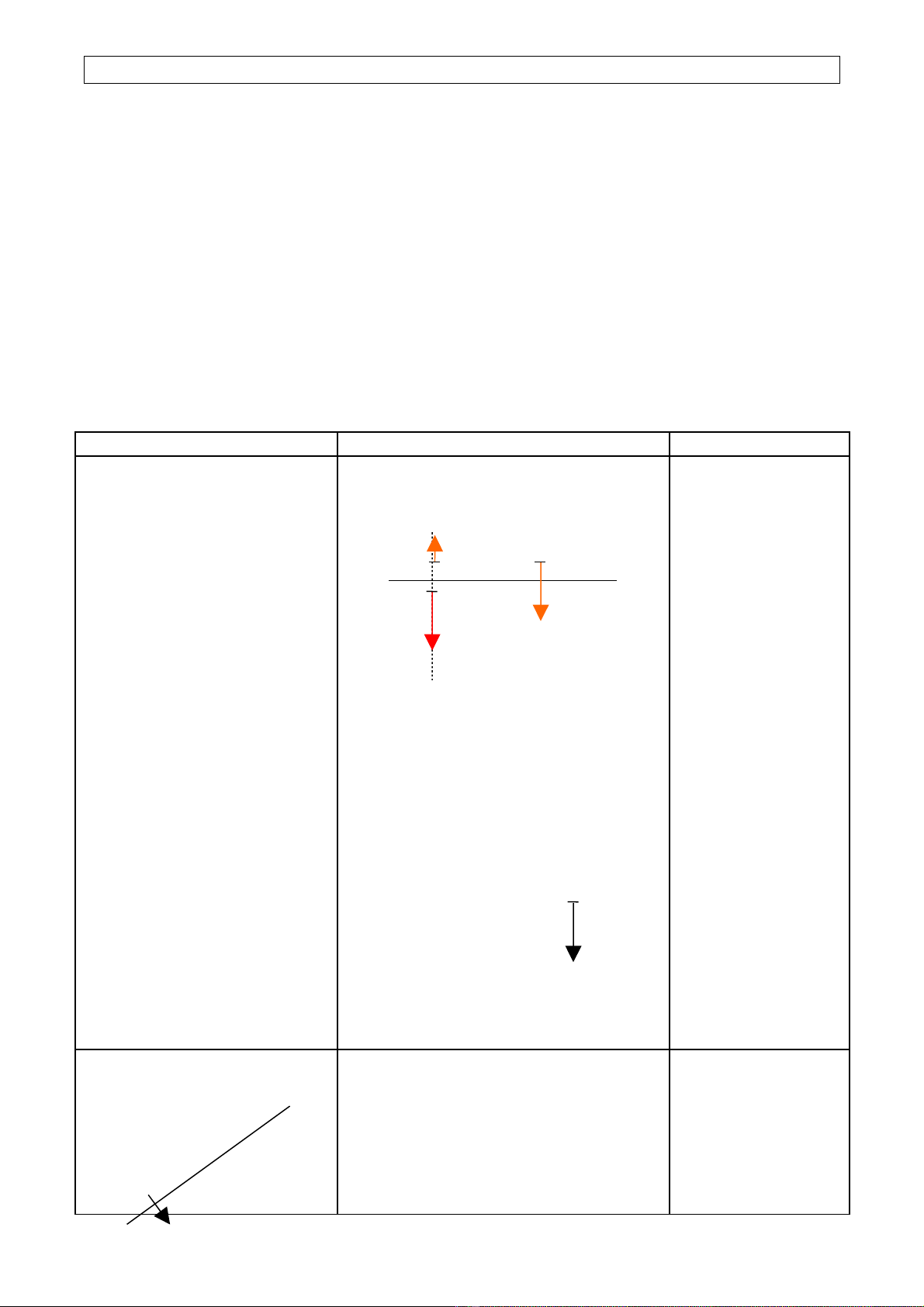
*Cho hình v :ẽ
*Yêu c u h c sinh nh n xét các vectầ ọ ậ ơ
1 2 3
, ,n n n
ur uur uur
*GV đ nh nghĩa vtpt c a đ ng th ngị ủ ườ ẳ
*GV v thêm vài vtpt c a (D) và yêuẽ ủ
c u HS tr l i ầ ả ờ ?1
*Cho
Yêu c u HS v đ ng th ng đi qua Iầ ẽ ườ ẳ
và nh n ậ
n
r
làm vtpt và nh n xét sậ ố
đ ng th ng v đ cườ ẳ ẽ ượ
I.Ph ng trình t ngươ ổ
quát c a đ ngủ ườ
th ng:ẳ
1)Vect phápơ
tuy n c a đ ngế ủ ườ
th ng:ẳ
Đn,Hv : hìnhẽ
65 sgk
*HS v hình và gi i bài toánẽ ả *Btoán: Trong mp to đ cho I(ạ ộ
0 0
;x y
)
và
( )
; 0n a b ≠
r r
.G i (D) là đ ngọ ườ
th ng qua I và có vtpt ẳ
n
r
.Tìm đi uề
ki n c a xvà y đ M(x;y) n m trênệ ủ ể ằ
(D)
*Gv có th g i ý vài câu h i:ể ợ ỏ
Trang 1
(D
)
1
n
ur
2
n
uur
3
n
uur
n
r
.I
.
.
( )
;
o o
I x y
( )
;n a b
r

( )
0 0
2 2
( ) . 0
( ) ( ) 0
0(*)
0
M D IM n
a x x b y y
ax by c
a b
∈ ⇔ =
⇔ − + − =
⇔ + + =
+ ≠
uuur r
*HS gi i quy t ?3ả ế
*HS làm H1 sgk
*Hs gi i VDả
*HS gi i BT2 sgkả
a)Ox: y = 0
b)Oy: x = 0
c)y-yo=0
d)x-xo =0
e)xox-yoy=0
.
IM
uuur
và
n
r
nh th nào v i nhau?ư ế ớ
.Hai vect vuông góc v i nhau khiơ ớ
và ch khi nào?ỉ
(*) g i là PTTQ c a (D) ọ ủ
*GV c n l u ý HS đk ầ ư
2 2
0a b+ ≠
*Ví d :Vi t PTTQ c a các đ ngụ ế ủ ườ
th ng sau:ẳ
a)(D1)qua M(-1;4) và // (d) :2x+3y+7=0
b)(D2)qua M(-1;4) và vuông góc
(d2):x+3y-4=0
c)Trung tr c c a AB v i A(1;3); B(-ự ủ ớ
3;1)
d)Đ ng cao AH c a tam giác ABCườ ủ
v i A(4;3); B(2;7); C(-3;-8)ớ
*Sau khi HS gi i xong Vd a,b GV choả
HS nhân xét pt (D1) so v i (d) và (Dớ2)
so v i (dớ2)
*GV cho HS làm BT2 sgk
2)Ph ng trìnhươ
t ng quát c aổ ủ
đ ng th ng:ườ ẳ
Hình v : hình 66ẽ
sgk
(D)
0 0
( ; )
( ; )
quaI x y
vtptn a b
r
PTTQ c a (D) là:ủ
a(x-
0
x
)+b(y-
0
y
)=0
⇔
ax+by+c=0
v i c=-aớ
0
x
-b
0
y
và
2 2
0a b+ ≠
*VD:
*BT2 Sgk
Ho t đ ng 2:Tìm các d ng đ c bi t c a đ ng th ngạ ộ ạ ặ ệ ủ ườ ẳ
Ho t đ ng c a tròạ ộ ủ Ho t đ ng c a giáo viênạ ộ ủ N i dung c n ghiộ ầ
*HS gi i quy t Hả ế 2
c = 0: (d):ax+by a = 0:(d): by
+ c = 0
D song song ho c trùng Oxặ
b=0 :d: ax+c=0
d song song ho c trùng Oy =ặ
0 (d)qua O
*GV cho HS làm ph n Hầ2 sgk l n l tầ ượ
v i c = 0, a = 0, b = 0 trong m i tr ngớ ỗ ườ
h p cho HS v hình r i ợ ẽ ồ
nh n xétậ
3)các d ng đ cạ ặ
bi t c a ph ngệ ủ ươ
trình t ng quát:ổ
Ghi nh , hình v :ớ ẽ
SGK
Ho t đ ng 3: Vi t ph ng trình đ ng th ng theo đo n ch n.ạ ộ ế ươ ườ ẳ ạ ắ
Ho t đ ng c a tròạ ộ ủ Ho t đ ng c a giáo viênạ ộ ủ N i dung c n ghiộ ầ
*HS làm ph n H3ầ
a)(AB):bx+ay-ab=0
b) bx+ay-ab=0
( )
1 0
1
bx ay ab
ab ab
x y
a b
⇔ + = ≠
⇔ + =
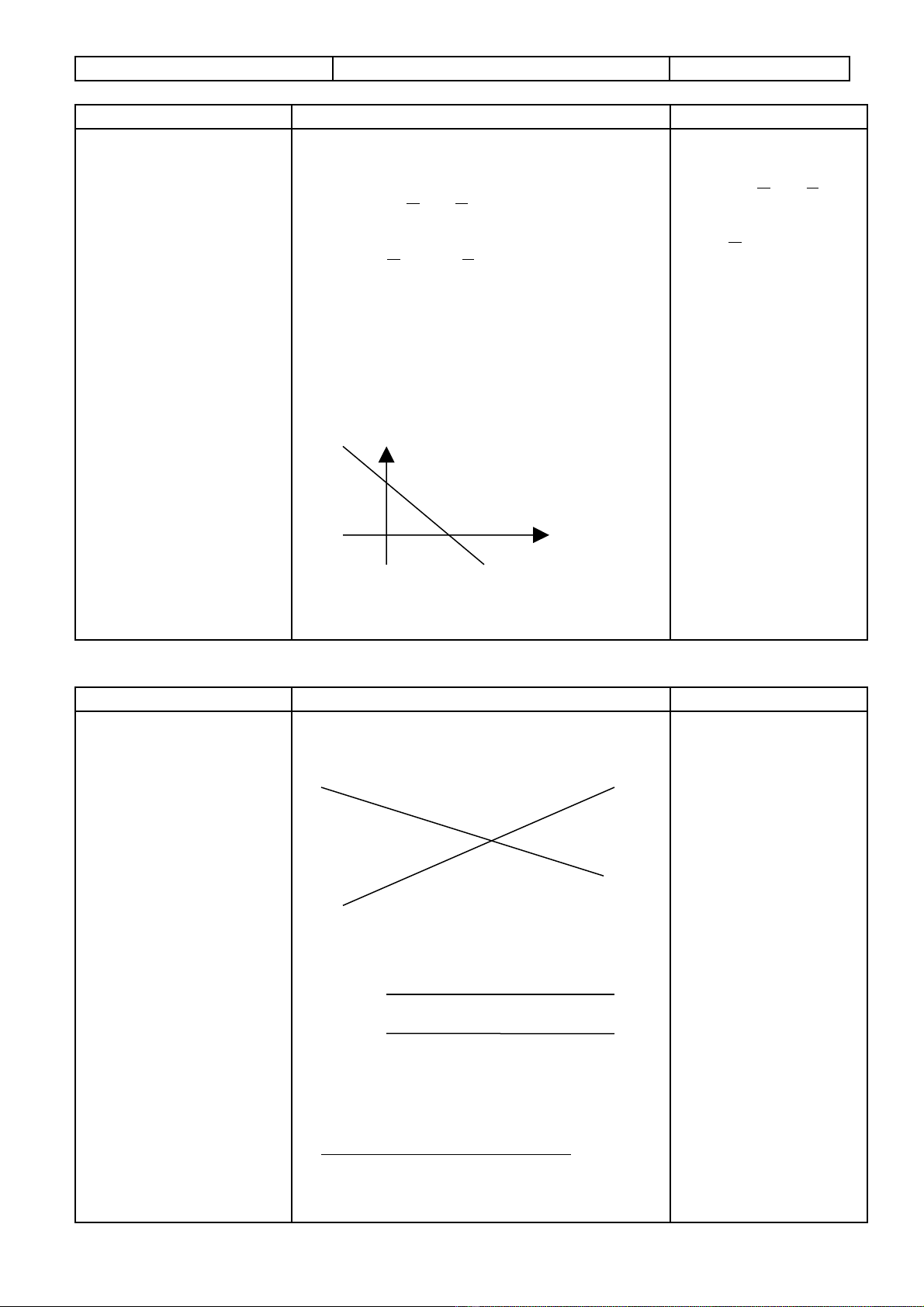
HS v n d ng công th c trênậ ụ ứ VD: Vi t ph ng trình đ ng th ngế ươ ườ ẳ
đi qua A(-1;0), B(0;2)
*Hình v Sgkẽ
Cho A(a;0), B(0;b)
( )
0ab ≠
( )
1 *
x y
a b
+ =
(*)g i là pt đ ngọ ườ
th ng theo đo nẳ ạ
ch n.ắ
Trang 2
tìm ph ng trình ABươ VD:
Ho t đ ng 4: Ph ng trình đ ng th ng theo h s gócạ ộ ươ ườ ẳ ệ ố
Ho t đ ng c a tròạ ộ ủ Ho t đ ng c a giáo viênạ ộ ủ N i dung c n ghiộ ầ
HS theo dõi và ghi chép
Hs gi i quy t ?5 Sgkả ế
*Cho d:ax+by+c=0(1)
N u ế
0b≠
( )
1a c
y x
b b
⇔ = − −
Đ t ặ
;
a c
k m
b b
= − = −
( ) ( )
1 2y kx m⇔ = +
(2) g i là ph ng trình c a d theo hsg, k:ọ ươ ủ
hsg
*ý nghĩa c a hsg: ủ
k tg
α
=
(
: 0
0
d ax by c
a c
y x b
b b
+ + =
⇔ = − − ≠
a
kb
= −
g i là hsgọ
c a đ ng th ng dủ ườ ẳ
*ý nghĩa c a hsg:ủ
Hình v sgkẽ
k tg
α
=
Ho t đ ng 5:xét v trí t ng đ i c a hai đ ng th ngạ ộ ị ươ ố ủ ườ ẳ
Ho t đ ng c a tròạ ộ ủ Ho t đ ng c a giáo viênạ ộ ủ N i dung c n ghiộ ầ
* Có 3 v trí t ngị ươ
đ i:c t nhau; song song;ố ắ
trùng nhau
*(D1) c t (Dắ2) : có 1
đi m chungể
*(D1)// (D2): không có
*Trong mp cho 2 đ ng th ng , gi a chúngườ ẳ ữ
có m y v trí t ng đ i?ấ ị ươ ố
*Nhậ
II.V trí t ng đ iị ươ ố
c a 2 đ ng th ng:ủ ườ ẳ
Cho
(D1):a1x+b1y+c1=0
(D2):a2x+b2y+c2=0
Xét hệ
1
2
( )
( )
pt D
pt D
(*)
. (*) có ngi m duyệ
nh t :(Dấ1) c t (Dắ2).
To đ giao đi mạ ộ ể
chính là nghi m c aệ ủ
h (*)ệ
.(*) vô nghi m :ệ
(D1)// (D2)
.(*) vô s nghi m:ố ệ
(D1)
≡
(D2)
*Chú ý:
Tr ng h p:aườ ợ 2,b2,c2
≠
0
Trang 3
α
O
x
y
D1
D2
D1
D2
D1,D2
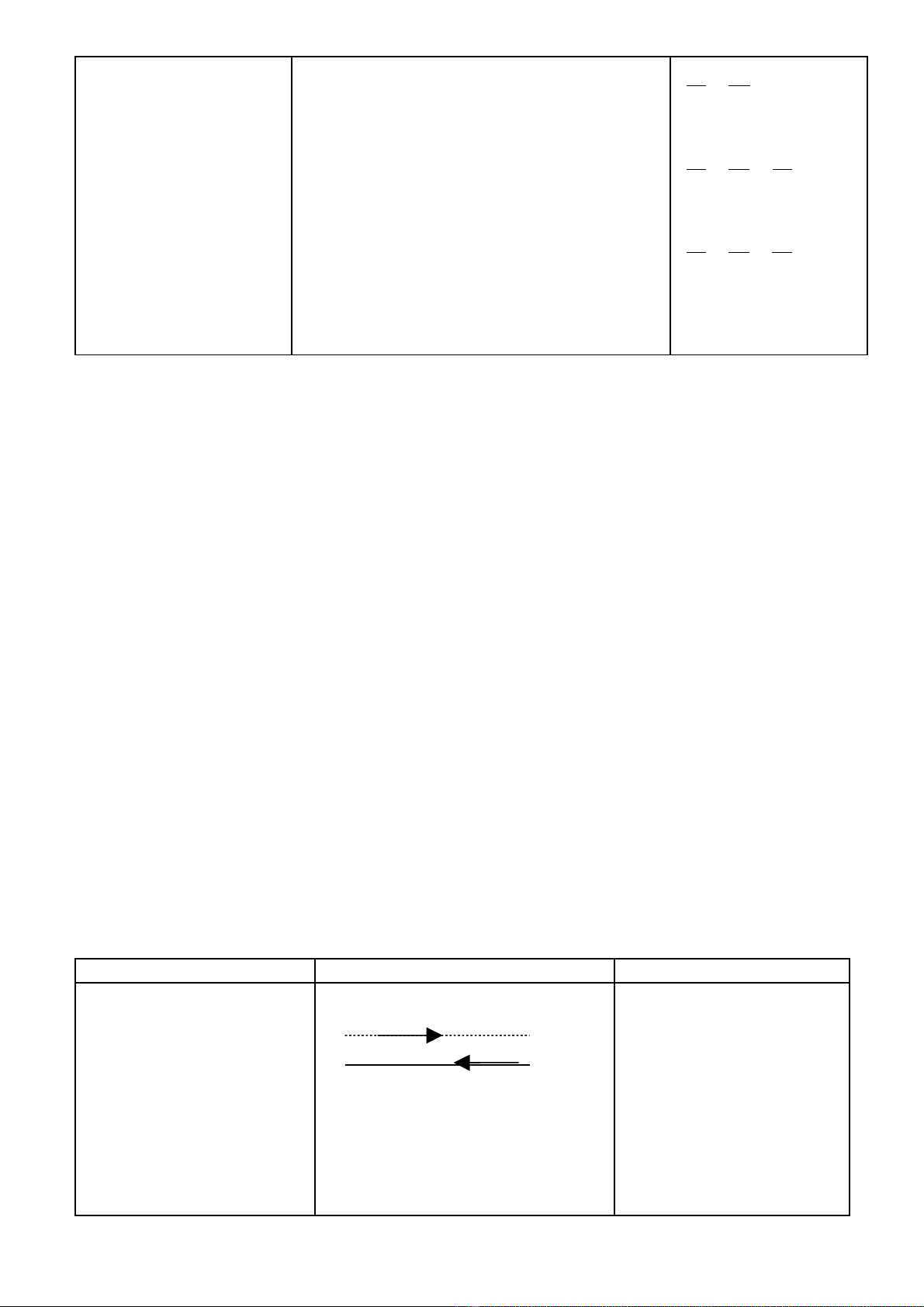
đi m chungể
*(D1) trùng (D2): vô số
đi m chungể
*HS gi i quy t ?6 và ?7ả ế
Sgk
*HS làm BT6 trang 80
Sgk
n xét s đi m chung c a (Dố ể ủ 1) và (D2) trong
t ng hình?ừ.
1 2
1 2
a a
b b
≠
:(D1)c tắ
(D2)
.
1 2 1
1 2 2
a a c
b b c
= ≠
:(D1)//
(D2)
.
1 2 1
1 2 2
a a c
b b c
= =
:(D1)
≡
(D2)
*BT6 Sgk
IV.C ng c :ủ ố
-PTTQ c a đ ng th ng(các d ng đ c bi t)ủ ườ ẳ ạ ặ ệ
-PT đ ng th ng theo đo n ch nườ ẳ ạ ắ
-PT đ ng th ng theo h s gócườ ẳ ệ ố
-Cách xét v trí t ng đ i c a 2 đ ng th ngị ươ ố ủ ườ ẳ
V.D n dò:BTVN:1,3,4 Sgk trang 80ặ
§2.PH NG TRÌNH THAM S C A Đ NG TH NG (2 TI T)ƯƠ Ố Ủ ƯỜ Ẳ Ế
I.M c tiêu:ụ
-HS l p đ c PTTS c a đ ng th ng khi bi t 1 đi m và m t VTCP c a nó. Ng c l i, tậ ượ ủ ườ ẳ ế ể ộ ủ ượ ạ ừ
PTTS c a đ ng th ng xác đ nh đ c VTCP c a nó và bi t đ c đi m(x;y) có thu củ ườ ẳ ị ựơ ủ ế ượ ể ộ
đ ng th ng đó hay khôngườ ẳ
-Th y đ c ý nghĩa c a tham s t trong ph ng trình là:m i giá tr c a tham s txác đ nhấ ượ ủ ố ươ ỗ ị ủ ố ị
to đ c a 1 đi mtrên đ ng th ng và ng c l i, m i đi m M(x;y) thu c đ ng th ng thìạ ộ ủ ể ườ ẳ ượ ạ ỗ ể ộ ườ ẳ
to đ c a nó xác đ nh m t giá tr t.ạ ộ ủ ị ộ ị
-Bi t chuy n t ph ng trình đ ng th ng d i d ng tham s sang d ng chính t c(n u có),ế ể ừ ươ ườ ẳ ướ ạ ố ạ ắ ế
sang d ng TQ và ng c l i.ạ ượ ạ
-Bi t s d ng MTBT(n u có)trong tính toán, gi i ph ng trình, h ph ng trình.ế ử ụ ế ả ươ ệ ươ
II.Chu n b ph ng ti n d y h c:ẩ ị ươ ệ ạ ọ
a)Th c ti n:ự ễ
b)Ph ng ti n:ươ ệ
c)Ph ng pháp:ươ
III.Ti n trình bài h c và các ho t đ ng:ế ọ ạ ộ
Ho t đ ng 1: Ki m tra bài cũ: G i HS lên b ngạ ộ ể ọ ả
S a các bài t p v nhà:1,3,4 trang 80 Sgkử ậ ề
Ho t đ ng 2: Khái ni m VTCP c a đ ng th ngạ ộ ệ ủ ườ ẳ
Ho t đ ng c a HSạ ộ ủ Ho t đ ng c a GVạ ộ ủ N i dungộ
*
1 2
, 0u u ≠
uuruur r
và có giá song
song ho c trùng v i (D)ặ ớ
*
n
r
và
u
r
đ u ề
0≠r
và
n u⊥
r r
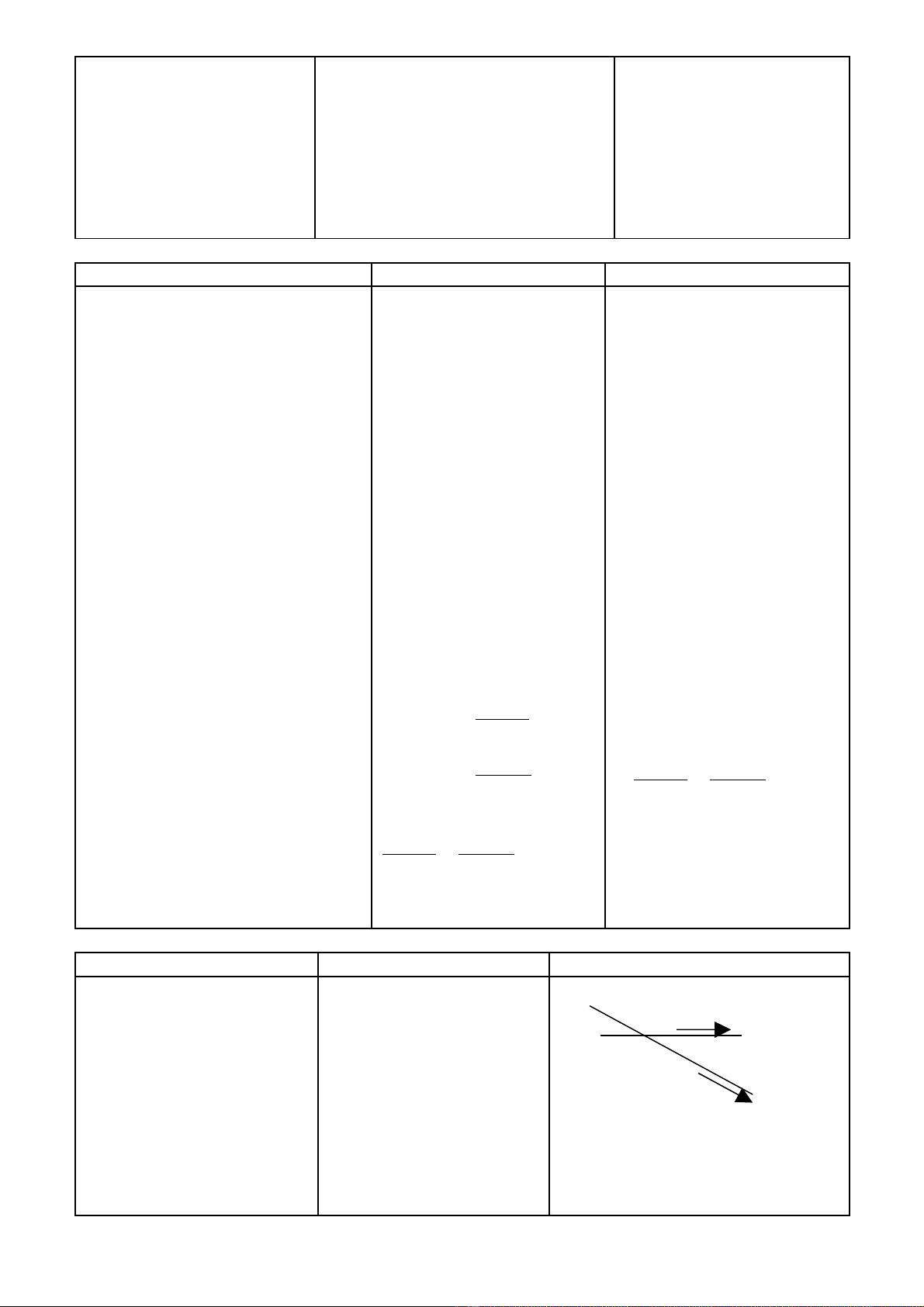
*Cho hình v :ẽ
Nh n xét các vect ậ ơ
1 2
,u u
uuruur
so v iớ
(D)?
Gv đ nh nghĩa VTCP c a đ ngị ủ ườ
I.Vect ch ph ng c aơ ỉ ươ ủ
đ ng th ng:ườ ẳ
Đn, Hv , Sgk trang 81ẽ
Trang 4
(D)
2
u
uur
1
u
r
*VTPT
n
r
(a;b)
u n u⊥ ⇒
r r r
(-b;a) hay
u
r
(b;-a)
*HS làm BT 8 trang 84
SGK
th ngẳ
*GV v thêm VTPT ẽ
n
r
c a (D) vàủ
yêu c u HS tr l i ?1ầ ả ờ
*Cho (D):ax+by+c=0. Tìm VTPT
và VTCP c a (D)?ủ
*L u ý:ư
(D) có VTPT
n
r
(a;b)
⇔
(D) có VTCP
u
r
(-b;a) hay
(b;-a)
*BT8 Sgk
Ho t đ ng 3: Vi t PTTS và PTCT c a đ ng th ngạ ộ ế ủ ườ ẳ
Ho t đ ng c a HSạ ộ ủ Ho t d ng c a GVạ ộ ủ N i dungộ
*HS v hình và gi i bài toánẽ ả
*
IM
uuur
và
u
r
cùng ph ng v iươ ớ
nhau
IM tu⇔ =
uuur r
(t là s th c)ố ự
⇔
02 2
0
( 0)
x x at a b
y y bt
= +
⇔ + ≠
= +
*HS tr l i ?3 và gi i bài t p H2ả ờ ả ậ
Sgk
*HS làm BT VD Sgk
*HS làm BT H3 Sgk
Bài toán:Trong mp to đạ ộ
Oxy cho (D) đi qua I(x0;y0)
và có VTCP
u
r
=(a;b). Tìm
đi u ki n c a x và y đề ệ ủ ể
M(x;y) thu c (D)ộ
*Các câu h i g i ý:ỏ ợ
.
IM
uuur
và
u
r
nh th nàoư ế
v i nhau?ớ
. Đi u ki n đ 2 vectề ệ ể ơ
cùng ph ng?ươ
*Trong PTTS c a (D)ủ
1 giá tr c a tị ủ
↔
M(x0;y0)
∈
(D)
*Cho (D):
0
0
x x at
y y bt
= +
= +
N u aế
≠
0, b
≠
0
Pt(1)
0
x x
ta
−
⇒ =
Pt(2)
0
y y
tb
−
⇒ =
V y ta có:ậ
0 0
x x y y
a b
− −
=
(*)
(*) g i là PTCT c a (D)ọ ủ
II.Ph ng trình tham sươ ố
c a đ ng th ng:ủ ườ ẳ
Hv : Sgkẽ
(D)
0 0
( ; )
( ; )
quaI x y
vtcpu a b
r
(D) có PTTS là:
02 2
0
( 0)
x x at a b
y y bt
= +
+ ≠
= +
•N u aế
0≠
, b
0≠
(D) có PTCT là
0 0
x x y y
a b
− −
=
•N u a=0 ho c b=0 thìế ặ
(D) không có PTCT
Ho t đ ng 4:Gi i bài t p xét v trí t ng đ i c aạ ộ ả ậ ị ươ ố ủ 2 đ ng th ngườ ẳ
Ho t đ ng c a HSạ ộ ủ Ho t đ ng c a GVạ ộ ủ N i dungộ
a)
( )
( )
1
2
2;1
6; 3
u
u
−
−
ur
uur
*GV v hình các tr ngẽ ườ
h p r i h ng d n HSợ ồ ướ ẫ
cách xét vi trí t ng đ iươ ố
c a 2 đ ng th ng d aủ ườ ẳ ự
vào 2 VTCP
*BT11 Sgk trang 84
Xét v trí t ng đ i c aị ươ ố ủ
các đ ng th ng sau:ườ ẳ
1
u
ur
và
2
u
uur
không cùng ph ng:(dươ 1)
và (d2) c t nhau.ắ
Trang 5
d1d2
1
u
ur
2
u
uur


























