Sử dụng các mô hình phân lớp, cảnh báo sớm rủi ro phá sản của doanh nghiệp, thông qua báo cáo tài chính, bằng chứng thực nghiệm tại Việt Nam

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:17

Thêm vào BST

Báo xấu

20
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Nghiên cứu sử dụng một số Mô hình phân lớp để giải quyết vấn đề này; việc xử lý kết quả được thông qua ngôn ngữ lập trình Python. Bước đầu đạt kết quả khả quan và đáng tin cậy thông qua bằng chứng thực nghiệm tại Việt Nam.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Sử dụng các mô hình phân lớp, cảnh báo sớm rủi ro phá sản của doanh nghiệp, thông qua báo cáo tài chính, bằng chứng thực nghiệm tại Việt Nam

SỬ DỤNG CÁC MÔ HÌNH PHÂN LỚP, CẢNH BÁO SỚM RỦI RO PHÁ SẢN CỦA DOANH NGHIỆP, THÔNG QUA BÁO CÁO TÀI CHÍNH, BẰNG CHỨNG THỰC NGHIỆM TẠI VIỆT NAM TS Nguyễn Huy Hoàng* Nguyễn Tâm Nhi* TÓM TẮT Trong quá trình hoạt động, có thể một số Doanh nghiệp gặp phải rủi ro dẫn đến phá sản; Việc dự báo sớm được khả năng này sẽ giúp ích cho Doanh nghiệp cũng như các Nhà quản lý, Nhà đầu tư. Thông tin hoạt động Doanh nghiệp chủ yếu dựa vào báo cáo tài chính (BCTC), nên việc xây dựng Mô hình cảnh báo sớm, rủi ro phá sản Doanh nghiệp thông qua thông tin báo cáo tài chính là khả thi và hữu dụng. Nghiên cứu sử dụng một số Mô hình phân lớp để giải quyết vấn đề này; việc xử lý kết quả được thông qua ngôn ngữ lập trình Python. Bước đầu đạt kết quả khả quan và đáng tin cậy thông qua bằng chứng thực nghiệm tại Việt Nam. Từ khóa: Phá sản doanh nghiệp; Báo cáo tài chính; Mô hình phân lớp; Python. 1. Giới thiệu các kiến thức cơ bản Các nhân tố, mô hình và phương pháp trong nghiên cứu Biến phụ thuộc Biến phụ thuộc trong mô hình dự báo rủi ro phá sản của doanh nghiệp là một biến nhị phân. Nghiên cứu thực hiện thu thập số liệu theo 2 khung thời gian của các doanh nghiệp, cụ thể như sau: + 4 quý: Đối với các doanh nghiệp đã phá sản, chọn quý thứ nhất là từ thời điểm phá sản và 3 quý còn lại là từ thời điểm phá sản trở về trước. Đối với các doanh nghiệp đang hoạt động, nghiên cứu chọn 4 quý từ quý III năm 2019 đến quý II năm 2020. + 8 quý: Đối với các doanh nghiệp đã phá sản, chọn quý thứ nhất là từ thời điểm phá sản và 7 quý còn lại là từ thời điểm phá sản trở về trước. Đối với các doanh nghiệp đang hoạt động, nghiên cứu chọn 8 quý từ quý IV năm 2018 đến quý II năm 2020. Khoa Kinh tế – Luật, Trường Đại học Tài chính – Marketing. * - 235
Biến phụ thuộc được xác định như sau: đối với các doanh nghiệp đã phá sản tại một thời điểm xác định sẽ được gán nhãn với giá trị “1”; ngược lại, đối với các doanh nghiệp hoạt động tại một thời điểm xác định sẽ được gán nhãn với giá trị “0”. Mô hình sau khi dự báo sẽ cho xác suất phá sản cho từng đối tượng, tùy thuộc vào ngưỡng phân loại riêng của mỗi nghiên cứu. Từ đó, có thể sắp xếp rủi ro phá sản vào các lớp phù hợp. Doanh nghiệp có xác suất phá sản lớn hơn ngưỡng phân loại sẽ được xếp vào lớp “1” và ngược lại sẽ được xếp vào lớp “0”. Các biến độc lập Nghiên cứu sử dụng 7 biến độc lập (thông tin trong BCTC) trong bảng dưới đây: Bảng 1. Các biến của mô hình STT Biến Z1 Lợi nhuận sau thuế Z2 Tổng tài sản Z3 Nợ phải trả Z4 Vốn chủ sở hữu Z5 P/E Z6 ROA Z7 ROE Trong nhiều tình huống cuộc sống, dự báo các phản ứng định tính là một nhu cầu cần thiết, quá trình dự báo này được gọi là phân lớp (classification). Các phương thức được sử dụng để phân lớp trước tiên dự báo xác suất xuất hiện từng lớp của một biến định tính, làm cơ sở để thực hiện phân loại. Có nhiều kỹ thuật để xây dựng một mô hình phân lớp, dự báo một phản ứng định tính. Nghiên cứu này sử dụng một số các thuật toán phân lớp được sử dụng phổ biến nhất: Logistic Regression; Random forest;… Xử lý kết quả bằng ngôn ngữ lập trình Python. Các thuật toán này xác định xác suất phá sản của từng đối tượng, từ đó dự báo sớm doanh nghiệp phá sản và doanh nghiệp hoạt động. Mô hình Logistic Regression Mô hình Logistic Regression ra đời vào những năm 1970 bởi Giáo sư David Roxbee Cox. Logistic Regression nghiên cứu sự tác động của các biến độc lập (liên tục hoặc rời rạc) đến biến phụ thuộc nhị phân (chỉ nhận một trong 2 giá trị: 0 hoặc 1). Một số khái niệm liên quan đến mô hình Logistic Regression: Odds ratio Tỷ lệ Odds được định nghĩa là tỉ số của xác suất biến cố xảy ra trên xác suất biến cố không/chưa xảy ra. Giá trị của xác suất dao động trong khoảng 0 đến 1, nhưng giá trị của Odds thì không có giới hạn và là một biến liên tục. 236 -
x Odds = N–x Trong đó: + N: không gian mẫu + x: số lượng biến cố xảy ra Logit của một biến cố Gọi P là xác suất xảy ra biến cố: x P= N Logit của một biến cố là log của tỷ lệ Odds: P logit(P) = log( = log(Odds) 1–P Mô hình Logistic Regression có biến phụ thuộc là logit(P). Do đó, để mô hình mối liên quan giữa rủi ro phá sản của doanh nghiệp và các biến độc lập, mô hình Logistic Regression có thể viết lại thành: logit(P) = α + β1X1 + β2X2 + β3X3 + ... + βnXn exp(α + β1X1 + β2X2 + β3X3 + ... + βnXn) ⇒P= 1 + exp(α + β1X1 + β2X2 + β3X3 + ... + βnXn) Khi đó, P là xác suất biến phụ thuộc (xác suất phá sản) nhận giá trị bằng 1 (có nguy cơ phá sản) và 1 – P là xác suất biến phụ thuộc nhận giá trị bằng 0 (không có nguy cơ phá sản). Random forest Từ thế kỷ XX, các nhà khoa học dữ liệu đã nghiên cứu cách để kết hợp nhiều thuật toán phân lớp thành tập hợp các thuật toán phân lớp để tăng độ chính xác so với chỉ sử dụng một thuật toán duy nhất. Mục đích của các thuật toán kết hợp là giảm lỗi phương sai và độ lệch (variance và bias) của các thuật toán. Bias là lỗi của mô hình học, còn variance là lỗi do tính biến thiên của mô hình so với tính ngẫu nhiên của các mẫu dữ liệu. 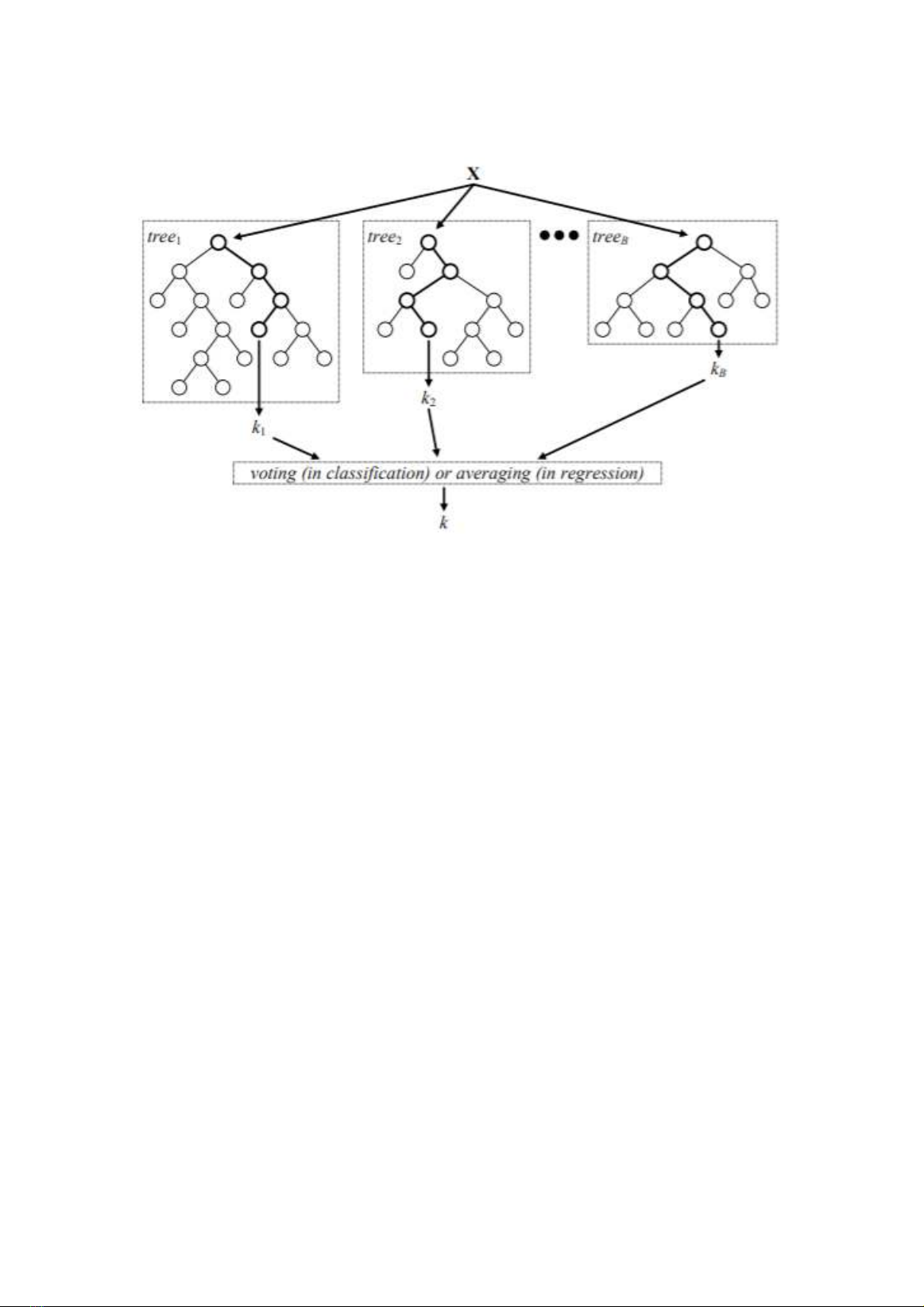Random forest được nghiên cứu (Breiman 2001) vì lý do trên. Đây là một trong những thuật toán kết hợp thành công nhất. Random forest xây dựng các cây không cắt nhánh nhằm giữ cho bias thấp và dùng tính ngẫu nhiên để điều khiển tính tương quan thấp giữa các cây trong rừng. Random forest tạo ra một tập hợp các cây quyết định không cắt - 237
tỉa, mỗi cây được xây dựng trên cơ sở lấy mẫu ngẫu nhiên có hoàn lại. Lỗi tổng quát của rừng phụ thuộc vào độ chính xác của từng cây thành viên trong rừng. Hình 1. Random forest minh hoạ Nguồn: Verikas et al. (2016) Các bước xây dựng Random forest: – Bước 1: Từ tập dữ liệu ban đầu S, sử dụng kỹ thuật lấy mẫu ngẫu nhiên có hoàn lại để tạo ra k tập dữ liệu con S = {S1, S2,…,Sk}. – Bước 2: Trên mỗi tập dữ liệu Si, xây dựng một cây quyết định Di. Thuật toán Random forest là thuật toán D = {Di}ki=1. Thay vì sử dụng tất cả các biến để lựa chọn điểm chia tốt nhất, tại mỗi nút rừng ngẫu nhiên chọn ngẫu nhiên một không gian tập con K’ biến từ K biến ban đầu (K’
Bắt đầu từ một nút duy nhất chứa tất cả dữ liệu huấn luyện, dữ liệu được chia thành hai nút bằng cách đặt câu hỏi nhị phân “nếu – thì – ngược lại”. Ví dụ, nếu tuổi của khách hàng được so sánh với 30 để đưa ra quyết định phân nhánh. Sau khi phân nhánh, các khách hàng dưới 30 tuổi đều ở cùng một nút trong khi các khách hàng có tuổi từ 30 trở lên nằm ở nút còn lại. Kích thước của cây có thể phát triển để thích ứng với sự phức tạp của vấn đề phân loại (Alpaydin 2010). Khi các nút lá thỏa mãn một số chỉ số như Gini và Entropy, quá trình phân nhánh dừng lại và quá trình cắt tỉa cây có thể được thực hiện để đơn giản hóa cây bằng cách cắt tỉa và loại bỏ các biến không cung cấp những thông tin mới đáng kể cho việc phân loại. Khác với các kỹ thuật học máy như Mạng Neural nhân tạo hoặc Bayesian, cây quyết định có thể cung cấp một lời giải thích dễ hiểu cho lý do đưa ra quyết định của nó. Sau khi việc phân loại được thực hiện và một khách hàng đã được phân loại bởi cây quyết định này, cán bộ tín dụng có thể theo dõi tất cả các câu hỏi được trả lời bởi các biến số của khách hàng này (ví dụ thông tin nhân khẩu hoặc giao dịch) để hiểu được lý do khách hàng được cây quyết định dán nhãn là tốt hoặc xấu. Có nhiều thuật toán được sử dụng để xây dựng cây quyết định, phổ biến như: – Thuật toán ID3 (Iterative Dichotomiser 3): được phát triển vào năm 1986 bởi Ross Quinlan. ID3 được áp dụng cho các bài toán phân lớp mà tất cả các biến đều ở dạng biến định tính. Thuật toán tạo ra một cây nhiều đường, tìm kiếm cho mỗi nút (thuật toán tham lam), tính năng phân loại của thuật toán sẽ mang lại mức tăng thông tin lớn nhất cho các mục tiêu phân loại. Cây được trồng với kích thước tối đa và sau đó một bước cắt tỉa được áp dụng để cải thiện hiệu quả của cây. – Thuật toán C4.5: là thuật toán kế thừa ID3, được Quinlan phát triển vào năm 1993. C4.5 sử dụng cơ chế lưu trữ dữ liệu thường trú trong bộ nhớ, do đó C4.5 chỉ thích hợp với những cơ sở dữ liệu nhỏ. – Thuật toán C5.0: là phiên bản mới nhất của Quinlan, theo giấy phép độc quyền. C5.0 sử dụng ít bộ nhớ hơn và xây dựng các quy tắc nhỏ hơn so với thuật toán C4.5, nhưng độ chính xác cao hơn. – Thuật toán CART (Classification and Regression Trees): ra đời năm 1984 bởi một nhóm các nhà thống kê (Breiman, Friedman, Olshen và Stone) đã xuất bản sách “Classification and Regression Trees”. CART rất giống với C4.5, nhưng nó hỗ trợ cho cả các biến đầu ra dạng hồi quy. CART xây dựng cây nhị phân bằng cách sử dụng các biến và ngưỡng phân loại có mức tăng thông tin lớn nhất tại mỗi nút. - 239
Gradient Boosting Boosting đề cập đến một họ các thuật toán có khả năng chuyển đổi những bộ học yếu thành những bộ học mạnh. Nguyên tắc chính của việc thúc đẩy (boosting) là để khớp với một chuỗi các mô hình các bộ học yếu, chỉ tốt hơn một chút so với đoán ngẫu nhiên. Gradient Boosting Tree là một dạng tổng quát của Boosting, được áp dụng trên cơ sở phương pháp tùy chỉnh hàm mất mát. Nó có thể dùng cho cả hai vấn đề hồi quy và phân loại. Gradient Boosting xây dựng mô hình theo một cách tuần tự. Fm(x) = Fm – 1(x) + γmhm(x) Tại mỗi giai đoạn, cây quyết định hm(x) được chọn để tối thiểu hóa hàm mất mát L cho mô hình hiện tại Fm – 1(x): Các thuật toán hồi quy và phân loại khác nhau thì sử dụng kiểu hàm mất mát tương ứng. Fm(x) = Fm – 1(x) + arguminh ∑ L(yi, Fm – 1(xi ) + ni = 1h(xi) Phương pháp đánh giá mô hình Trong bài nghiên cứu này, mô hình dự báo khả năng phá sản của doanh nghiệp được chuyển thành lớp nhị phân. Nghiên cứu ký hiệu P cho lớp tích cực và N cho lớp tiêu cực, tương đương với doanh nghiệp hoạt động (gắn nhãn là 0) và doanh nghiệp phá sản (gắn nhãn là 1). Mô hình được học và đào tạo dự báo và phân loại thành P hoặc N. Bảng 2 dưới đây là ma trận nhầm lẫn (Confusion matrix), thể hiện kết quả dự báo của mô hình. Bảng 2. Ma trận nhầm lẫn (Confusion matrix) Actual/True class 0 1 0 True Positive (TP) False Positive (FP) Predicted class 1 False Negative (FN) True Negative(TN) Accuracy, Recall and Precision Để đánh giá độ hiệu quả của mô hình phân loại, nghiên cứu sử dụng các chỉ số Accuracy, Recall and Precision. Accuracy là chỉ số đơn giản và được sử dụng rộng rãi để đánh giá mô hình phân lớp. Ngoài ra, Recall và Precision cũng là 2 chỉ số được sử dụng để kiểm tra độ chính xác của mô hình khi dữ liệu mất cân bằng (Juba and Le 2019). Bảng 3. Công thức các chỉ số Accuracy, Precision và Recall Chỉ số Công thức Accuracy TP + TN TP + TN + FP + FN 240 -
Chỉ số Công thức Precision TP TP + FP Recall TP TP + FN ROC và AUC Đường cong ROC (Receiver Operating Characteric) là một công cụ để đánh giá phổ biến (Obuchowski and Bullen 2018) trong các mô hình dự báo. Đây là một biểu đồ hai chiều, trục tung đại diện cho giá trị True Positive Rate ( TP/(TP + FN)) và trục hoành đại diện cho giá trị False Positive Rate (FP/(FP + TN)). Một mô hình có hiệu quả càng cao khi FPR thấp và TPR cao, tức là tại một điểm trên đường cong ROC gần với điểm tọa độ (0,1) trên đồ thị, đường cong càng gần thì mô hình càng hiệu quả. Tuy nhiên, việc so sánh hiệu suất cao của các mô hình bằng ROC là điều không thực sự dễ dàng và chính xác tuyệt đối. Để khắc phục nhược điểm này, AUC ( Area Under the Curve) là một công cụ chiếm ưu thế hơn. Đại lượng này chính là diện tích nằm dưới đường cong ROC và cụ thể AUC = ∫10ROC(t)dt (Hanley, J.A., & McNeil, 1982). Với giá trị AUC nằm giữa khoảng từ 0.5 đến 0.7 thì mô hình dự báo có độ chính xác thấp, nằm giữa khoảng từ 0.7 đến 0.9 thì mô hình dự báo có độ chính xác trung bình, trên 0.9 mô hình dự báo có độ chính xác cao (Streiner, D. L., Cairney, 2007). 2. Dữ liệu và các biến của mô hình Cơ sở dữ liệu của mô hình Số liệu tổng hợp 180 doanh nghiệp, cụ thể 90 doanh nghiệp phá sản và 90 doanh nghiệp đang hoạt động từ quý I năm 2005 đến quý II năm 2020.(nguồn Bộ Kế hoạch và Đầu tư);( xem phụ luc1) Chuẩn bị và xử lý dữ liệu Nghiên cứu có 2 biến phụ thuộc là doanh nghiệp phá sản và doanh nghiệp hoạt động. Trong trường hợp này, mô hình thực hiện gán nhãn cho biến phụ thuộc ứng với doanh nghiệp hoạt động bằng 0 và doanh nghiệp phá sản là 1. Theo (Oded Maimon 2012), một bộ dữ liệu bị mất cân bằng nếu biến phân lớp không được biểu diễn gần như bằng nhau. Dữ liệu bị mất cân bằng sẽ gây ảnh hưởng tiêu cực đến kết quả nghiên cứu. - 241
Từ biểu đồ phân phối biến phụ thuộc, có thể thấy tập dữ liệu huấn luyện mô hình bị mất cân bằng cao. Đối với khung thời gian 4 quý, nghiên cứu thu được 630 doanh nghiệp hoạt động (87.5%) và 90 doanh nghiệp phá sản (12.5%). Đối với khung thời gian 8 quý, nghiên cứu thu được 1350 doanh nghiệp hoạt động (87.5%) và 90 doanh nghiệp phá sản (6.25%). 4 Qúy 8 Quý Hình 2. Số quan sát của doanh nghiệp phá sản và doanh nghiệp hoạt động Để xử lý dữ liệu mất cân bằng, Nitesh V. Chawla, Kevin W. Bowyer, Lawrence O. Hall (2006) đã đề xuất kỹ thuật lấy mẫu quá mức tổng hợp SMOTE (Synthetic Minority Over-sampling Technique). Thuật toán SMOTE xây dựng dữ liệu dựa trên sự tương đồng về không gian biến giữa các mẫu thiểu số hiện có. Cụ thể, đối với tập hợp con Smin ϵ S, sử dụng thuật toán K-nearest neighbors cho mỗi ví dụ xi ϵ Smin, với một số số nguyên K được chỉ định, các lân cận K gần nhất được định nghĩa là các phần tử K của Smin có khoảng cách giữa nó và xi có cường độ nhỏ nhất theo kích thước n của không gian biến X. Để tạo mẫu tổng hợp, chọn ngẫu nhiên một trong các mẫu K gần nhất, sau đó nhân hiệu số vectơ đặc trưng tương ứng với một số ngẫu nhiên trong khoảng [0, 1], và cuối cùng, thêm vectơ vào xi. xnew = xi + ( i – xi) × δ Trong đó: xi ϵ Smin là ví dụ thiểu số đang được xem xét, i là một trong những phần tử gần nhất của K cho xi: ϵ Smin và δ ϵ [0, 1] là một số ngẫu nhiên. Các kỹ thuật thay đổi cỡ mẫu chỉ được áp dụng cho tập dữ liệu huấn luyện (train set), tập kiểm tra (test set) phải được giữ nguyên để đảm bảo độ chính xác của mô hình nghiên cứu. Trong Python, thư viện “Imblearn” cung cấp mô-đun “Over_sampling.SMOTE” để tạo tập dữ liệu theo phương pháp lấy mẫu quá mức tổng hợp SMOTE. Sau khi áp dụng cho bộ dữ liệu huấn luyện, dữ liệu mới có phân phối biến phụ thuộc như sau: 242 -
Bảng 4. Số quan sát của nghiên cứu khi sử dụng kỹ thuật SMOTE 4 Quý 8 Quý Hoạt động Phá sản Hoạt động Phá sản 630 630 1350 1350 3. Kết quả nghiên cứu Để đánh giá hiệu quả của các mô hình nghiên cứu, chúng tôi đã tiến hành hậu kiểm bằng các mô hình phân lớp, sau khi đã xây dựng và tối ưu hoá các tham số của mô hình. Nghiên cứu tiến hành đánh giá hiệu quả của các mô hình dự báo theo các chỉ số đã đề cập dựa trên sự hỗ trợ từ thư viện Scikit-learn của Python. 3.1. Đánh giá mô hình bằng Logistic Regression Bảng 5. Ma trận nhầm lẫn của trận mô hình Logistic Regression 4 Quý 8 Quý Predict 0 1 0 1 0 138 38 0 309 91 Actual 1 45 157 1 70 340 Nguồn: Kết quả tính toán từ phần mềm Python Đối với khung thời gian 4 quý, bằng kỹ thuật Over_sampling.SMOTE, bài nghiên cứu có 1260 quan sát. Từ đó, nghiên cứu phân tách số liệu một cách ngẫu nhiên thành 2 phần: 70% training và 30% testing, nghĩa là trong đó có 882 số quan sát thuộc phần dữ liệu training và 378 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Logistic Regression đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Logistic Regression bằng 295. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 138 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 157 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 20%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 45 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 38 quan sát (False Negative). Đối với khung thời gian 8 quý, bài nghiên cứu có 2700 quan sát. Từ đó, nghiên cứu phân tách số liệu một cách ngẫu nhiên thành 2 phần: 70% training và 30% testing, nghĩa là trong đó có 1890 số quan sát thuộc phần dữ liệu training và 810 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Logistic Regression đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Logistic Regression bằng 639. Trong đó, số doanh nghiệp - 243
dự báo đúng là đang hoạt động là 309 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 340 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 20%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 70 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 91 quan sát (False Negative). Dựa vào kết quả của ma trận nhầm lẫn, nghiên cứu thu được chỉ số Accuracy, Precision và Recall như bảng 6 sau: Bảng 6. Accuracy, Precision và Recall của mô hình Logistic Regression 4 Quý 8 Quý Accuracy 78.04% 80.12% Recall 78.41% 77.25% Precision 75.41% 81.53% Nguồn: Kết quả tính toán từ phần mềm Python Trong mô hình Logistic Regression với thời gian 8 quý, nghiên cứu thu được chỉ số Accuracy bằng 80.12% cao hơn thời gian 4 quý 2.08%. Bên cạnh đó, chỉ số Precision trong thời gian 8 quý cũng bằng 81.53%, đây chính là tỷ lệ dự báo đúng doanh nghiệp đang hoạt động trên cho tổng doanh nghiệp dự báo đúng là đang hoạt động và doanh nghiệp dự báo là đang hoạt động nhưng thực tế là đã phá sản. Đồng thời, chỉ số này cũng cao hơn trong thời gian 4 quý là 6.12%. Đối với chỉ số Recall với mô hình 4 quý bằng 78.41% cao hơn mô hình quy mô 8 quý 1.16%, đại diện cho tỷ lệ dự báo đúng doanh nghiệp đang hoạt động trên cho tổng dự báo đúng doanh nghiệp đang hoạt động và doanh nghiệp dự báo là phá sản nhưng thực tế là đang hoạt động. 4 Quý 8 Quý Hình 3. Kết quả đường cong ROC và diện tích AUC của mô hình Logistic Regression 244 -
Nguồn: Kết quả tính toán từ phần mềm Python Đường cong ROC chính là một công cụ thể hiện sự hiệu quả của mô hình tại các ngưỡng phân loại khác nhau. Hình 7 biểu diễn đường cong ROC với diện tích AUC thu được tại thời điểm 4 quý và thời điểm 8 quý khá tương đồng nhau lần lượt ứng với AUC = 0.85 và AUC = 0.86 3.2. Đánh giá mô hình bằng Decision tree Bảng 7. Ma trận nhầm lẫn mô hình Decision Tree 4 Quý 8 Quý Predict 0 1 0 1 0 155 24 0 375 31 Actual 1 20 179 1 18 386 Đối với khung thời gian 4 quý, bằng kỹ thuật Over_sampling.SMOTE, bài nghiên cứu có 1260 quan sát. Từ đó, nghiên cứu phân tách số liệu một cách ngẫu nhiên thành 2 phần: 70% training và 30% testing, nghĩa là trong đó có 882 số quan sát thuộc phần dữ liệu training và 378 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Decision Tree đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Decision Tree bằng 334. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 155 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 179 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 12%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 20 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 24 quan sát (False Negative). Đối với khung thời gian 8 quý, bài nghiên cứu có 2700 quan sát. Từ đó, nghiên cứu phân tách số liệu một cách ngẫu nhiên thành 2 phần: 70% training và 30% testing, nghĩa là trong đó có 1890 số quan sát thuộc phần dữ liệu training và 810 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Logistic Regression đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Decision tree bằng 761. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 375 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 386 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 6 6%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 18 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 31 quan sát (False Negative). Dựa vào kết quả của ma trận nhầm lẫn, nghiên cứu thu được chỉ số Accuracy, Precision - 245
và Recall như bảng 8 sau: Bảng 8. Accuracy, Precision và Recall, AUC của mô hình Decision Tree 4 Quý 8 Quý Accuracy 88% 94% Recall 87% 92% Precision 89% 95% AUC 0.93 0.97 Nguồn: Kết quả tính toán từ phần mềm Python Trong mô hình Decision Tree với thời gian 8 quý, nghiên cứu thu được chỉ số Accuracy bằng 94% cao hơn thời gian 4 quý 6% Bên cạnh đó, chỉ số Precision trong thời gian 8 quý cũng bằng 95%, đây chính là tỷ lệ dự báo đúng doanh nghiệp đang hoạt động trên cho tổng doanh nghiệp dự báo đúng là đang hoạt động và doanh nghiệp dự báo là đang hoạt động nhưng thực tế là đã phá sản. Đồng thời, chỉ số này cũng cao hơn trong thời gian 4 quý là 6%. Đối với chỉ số Recall với mô hình 4 quý bằng 92% cao hơn mô hình quy mô 8 quý 5%, đại diện cho tỷ lệ dự báo đúng doanh nghiệp đang hoạt động trên cho tổng dự báo đúng doanh nghiệp đang hoạt động và doanh nghiệp dự báo là phá sản nhưng thực tế là đang hoạt động. Giá trị AUC đối với mô hình Decision Tree trong khung thời gian 8 quý là 0.97 cao hơn giá trị AUC đối với mô hình này trong khung thời gian 4 quý, cụ thể 0.93. Kết quả trên thể hiện khung thời gian 8 quý đem lại hiệu suất mô hình tốt hơn mô hình trong khung thời gian 4 quý. 3.3. Đánh giá mô hình bằng Random forest Bảng 9. Ma trận nhầm lẫn của mô hình Random forest 4 Quý 8 Quý Predict 0 1 0 1 0 144 35 0 358 48 Actual 1 8 191 1 15 389 Nguồn: Kết quả tính toán từ phần mềm Python Tương tự với mô hình Decision Tree 4 quý, đối với mô hình Random forest bài nghiên cứu cũng có 1260 quan sát, trong đó có 882 số quan sát thuộc phần dữ liệu training và 378 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Random forest đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Random forest bằng 335. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 144 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 191 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 246 -
11%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 8 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 35 quan sát (False Negative). Đối với khung thời gian 8 quý, bài nghiên cứu cũng có 2700 quan sát và trong đó có 1890 số quan sát thuộc phần dữ liệu training và 810 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Random forest đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Random forest bằng 747. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 358 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 389 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 7.8%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 15 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 48 quan sát (False Negative). Dựa vào kết quả của ma trận nhầm lẫn, nghiên cứu thu được chỉ số Accuracy, Precision và Recall như bảng 10 sau: Bảng 10. Accuracy, Precision và Recall, AUC của mô hình Random forest 4 Quý 8 Quý Accuracy 89% 92% Recall 80% 88% Precision 95% 96% AUC 0.95 0.98 Nguồn: Kết quả tính toán từ phần mềm Python Trong mô hình Random forest, nghiên cứu thu được kết quả chỉ số Accuracy đối với thời gian trong vòng 8 quý bằng 92% cao hơn thời gian trong vòng 4 quý gần 3%. Đồng thời chỉ số Recall và Precision trong khung thời gian 8 quý lần lượt là 88% và 96% và vượt trội hơn so với thời gian 4 quý lần lượt là 8% và 1%. Trong mô hình Random forest, diện tích AUC đối với khung thời gian 8 quý bằng 0.96 cao hơn khung thời gian 4 quý là 0.3. Kết quả trên thể hiện khung thời gian 8 quý đem lại hiệu suất mô hình tốt hơn mô hình trong khung thời gian 4 quý. 3.4. Đánh giá mô hình bằng Gradient Boosting Bảng 11. Ma trận nhầm lẫn của mô hình Gradient Boosting 4 Quý 8 Quý Predict 0 1 0 1 0 155 24 0 381 25 Actual 1 0 199 1 0 404 - 247
Nguồn: Kết quả tính toán từ phần mềm Python Đối với mô hình Gradient Boosting bài nghiên cứu cũng có 1260 quan, trong đó có 882 số quan sát thuộc phần dữ liệu training và 378 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Gradient Boosting đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Gradient Boosting bằng 354. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 155 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 199 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 6%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 0 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 24 quan sát (False Negative). Đối với khung thời gian 8 quý, bài nghiên cứu cũng có 2700 quan sát và trong đó có 1890 số quan sát thuộc phần dữ liệu training và 810 số quan sát thuộc phần dữ liệu testing. Xác suất thu được của mô hình Gradient Boosting đã được chuyển thành dự báo nhị phân: 1 nếu giá trị đó lớn hơn threshold = 0.5, và ngược lại thì bằng 0. Tổng kết quả dự báo đúng trong mô hình Gradient Boosting bằng 785. Trong đó, số doanh nghiệp dự báo đúng là đang hoạt động là 381 (True Positive) và doanh nghiệp dự báo phá sản chính xác là 404 (True Negative). Mặc khác, kết quả dự báo sai chiếm gần 3%, cụ thể: số doanh nghiệp dự báo là đang hoạt động nhưng thực tế đã phá sản là 0 quan sát (False Positive), số doanh nghiệp dự báo là phá sản nhưng thực tế là không chiếm 25 quan sát (False Negative). Dựa vào kết quả của ma trận nhầm lẫn, nghiên cứu thu được chỉ số Accuracy, Precision và Recall như bảng 12 sau: Bảng 12. Accuracy, Precision và Recall, AUC của mô hình Gradient Boosting 4 Quý 8 Quý Accuracy 94% 97% Recall 87% 94% Precision 100% 100% AUC 0.98 0.99 Nguồn: Kết quả tính toán từ phần mềm Python Trong mô hình Gradient Boosting, nghiên cứu thu được kết quả chỉ số Accuracy đối với thời gian trong vòng 8 quý bằng 97% cao hơn thời gian trong vòng 4 quý gần 3%. Đồng thời chỉ số Recall và Precision trong khung thời gian 8 quý lần lượt là 94% và 100% và vượt trội hơn so với thời gian 4 quý lần lượt là 7% và 0. Trong mô hình Gradient Boosting, diện tích AUC đối với khung thời gian 8 quý bằng 0.99 cao hơn khung thời gian 4 quý là 0.1. Kết quả trên thể hiện khung thời gian 8 quý đem lại hiệu suất mô hình tốt hơn mô hình trong khung thời gian 4 quý. 248 -
4. Thảo luận kết quả và kiến nghị Doanh nghiệp chính là hệ thống tuần hoàn của nền kinh tế, do đó việc dự báo rủi ro phá sản của doanh nghiệp là một phần vô cùng quan trọng của mọi quốc gia để góp phần ngăn chặn những kết quả xấu và có biện pháp hỗ trợ kịp thời. Bài nghiên cứu này đã tiến hành phân tích thực nghiệm và triển khai các mô hình nghiên cứu bao gồm Logistic Regression, Decision Tree, Random forest và Gradient Boosting trong hai thời khung thời gian 8 quý và 4 quý. Với 7 chỉ số tài chính trong báo cáo của 180 doanh nghiệp, cụ thể là 90 doanh nghiệp đang hoạt động và 90 doanh nghiệp phá sản với sự tương đồng về tổng giá trị tài sản để đảm bảo việc cân bằng tính chất bộ dữ liệu và giúp cho việc dự báo hiệu quả hơn. Kết quả nghiên cứu cho thấy rằng, mô hình Gradient Boosting trong khung thời gian 8 quý mang lại hiệu suất cao hơn so với các mô hình còn lại thể hiện qua các chỉ số Accuracy (97%), Precision (100%), Recall (94%) và AUC (0.99). Nghiên cứu này, là một nguồn thông tin hữu ích dành cho các nhà quản lý, đầu tư và các cơ quan nhà nước tham khảo và áp dụng vào việc kiểm soát tình hình hoạt động của các doanh nghiệp. Đồng thời, việc đánh giá và xem xét các hiệu suất của từng mô hình ứng với từng khung thời gian khác nhau cũng là một vấn đề cần chú trọng để giúp cho việc nâng cao chất lượng, thúc đẩy quá trình phát triển và phòng tránh rủi ro phá sản của doanh nghiệp. Mô hình đánh giá hiệu quả của các thuật toán tại ngưỡng phân loại 50%. Tuy nhiên trên thực tế, việc điều chỉnh ngưỡng phân loại trên cũng có thể làm tăng độ chính xác và mức độ phù hợp cho mô hình. Trong tương lai, đề tài nghiên cứu mong muốn sẽ cải thiện bộ số liệu với các chỉ số tài chính đa dạng hơn và áp dụng nhiều phương pháp hiệu quả, đa dạng hơn nữa như XG Boost, Support Vector Machine. TÀI LIỆU THAM KHẢO Altman, Edward, I. (1974). Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. The Journal of Finance, 29(1), 312-312. Beaver, William H. (1966). Financial Ratios as Predictors of Failure. Journal of Accounting Research, 4, 71-111. Betz, Frank, Silviu Oprică, Tuomas A. Peltonen, & Peter Sarlin. (2013). Wo r k i n g Pa P e r S e r i e S Predicting DiStreSS in EuroPean BankS, (159). Breiman, Leo. (2001). Random Forests. Machine Learning. Carmona, Pedro, Francisco Climent, & Alexandre Momparler (2019). Predicting Failure in the U.S. Banking Sector: An Extreme Gradient Boosting Approach. International Review of Economics and Finance, 61, 304-23. Couronné, Raphael, Philipp Probst, & Anne Laure Boulesteix. (2018). Random Forest versus Logistic Regression: A Large-Scale Benchmark Experiment. BMC Bioinformatics, 19(1). - 249
Demyanyk, Yuliya, & Iftekhar Hasan. (2010). Financial Crises and Bank Failures: A Review of Prediction Methods. Omega, 38(5), 315-24. Foos, Daniel, Lars Norden, & Martin Weber. (2010). Loan Growth and Riskiness of Banks. Journal of Banking and Finance, 34(12), 2929-40. Ghenimi, Ameni, Hasna Chaibi, & Mohamed Ali Brahim Omri. (2017). The Effects of Liquidity Risk and Credit Risk on Bank Stability: Evidence from the MENA Region.” Borsa Istanbul Review, 17(4), 238-48. Gogas, Periklis, Theophilos Papadimitriou, & Anna Agrapetidou. (2018). Forecasting Bank Failures and Stress Testing: A Machine Learning Approach. International Journal of Forecasting, 34(3), 440-55. Hanley, J.A., & McNeil, B. J. (1982). The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology, 143, 29-36. Juba, Brendan, & Hai, S. Le (2019). Precision-Recall versus Accuracy and the Role of Large Data Sets. Proceedings of the AAAI Conference on Artificial Intelligence, 33, 4039-48. King, Dan. (2010). Predicting Bank Distress in the UK with Machine Learning. The College Mathematics Journal, 41(5), 416-18. Le, Hong Hanh, & Jean Laurent Viviani (2018). Predicting Bank Failure: An Improvement by Implementing a Machine-Learning Approach to Classical Financial Ratios. Research in International Business and Finance, 44(July), 16-25. Manthoulis, Georgios, Michalis Doumpos, Constantin Zopounidis, & Emilios Galariotis. (2020). An Ordinal Classification Framework for Bank Failure Prediction: Methodology and Empirical Evidence for US Banks. European Journal of Operational Research, 282(2), 786-801. Nguyễn Thị Tuyết Lan (2019). Các yếu tố ảnh hưởng đến rủi ro phá sản của doanh nghiệp xây dựng, 31-41. Nitesh V. Chawla, Kevin W. Bowyer, Lawrence O. Hall, W. Philip Kegelmeyer (2006). SMOTE: Synthetic Minority Over-Sampling Technique. Journal of Artificial Intelligence Research, 2009(Sept. 28), 321-57. Obuchowski, Nancy A., & Jennifer A. Bullen (2018). Receiver Operating Characteristic (ROC) Curves: Review of Methods with Applications in Diagnostic Medicine. Physics in Medicine and Biology, 63(7). Oded Maimon, & Lior Rokach (2012). Data Mining and Knowledge Discovery. Petropoulos, Anastasios, Vasilis Siakoulis, Evangelos Stavroulakis, & Nikolaos E. Vlachogiannakis (2020). Predicting Bank Insolvencies Using Machine Learning Techniques. International Journal of Forecasting (April 2017), 1-42. Ravi Kumar, P., & V. Ravi (2007). Bankruptcy Prediction in Banks and Firms via Statistical and Intelligent Techniques – A Review. European Journal of Operational Research, 180(1), 1-28. Rustam, Zuherman, & Glori Stephani Saragih (2018). Predicting Bank Financial Failures Using Random Forest. 2018 International Workshop on Big Data and Information Security, IWBIS 2018, 81-86. 250 -
Shrivastava, Santosh, P. Mary Jeyanthi, and Sarbjit Singh (2020). Failure Prediction of Indian Banks Using SMOTE, Lasso Regression, Bagging and Boosting. Cogent Economics and Finance, 8(1), 1-17. Streiner, D. L., & Cairney, J. (2007). What’s under the ROC? An Introduction to Receiver Operating Characteristic Curves. Canadian Journal Psychiatry, 52, 121-28. Tanaka, Katsuyuki, Takuji Kinkyo, & Shigeyuki Hamori (2016). Random Forests-Based Early Warning System for Bank Failures. Economics Letters, 148, 118-21. Tseng, Fang Mei, & Yi Chung Hu (2010). Comparing Four Bankruptcy Prediction Models: Logit, Quadratic Interval Logit, Neural and Fuzzy Neural Networks. Expert Systems with Applications, 37(3), 1846-53. Verikas, Antanas, Evaldas Vaiciukynas, Adas Gelzinis, James Parker, & M. Charlotte Olsson (2016). Electromyographic Patterns during Golf Swing: Activation Sequence Profiling and Prediction of Shot Effectiveness. Sensors (Switzerland), 16(4). Wang, Yi-Shu, Xue Jiang, & Zhen-Jia Liu (2016). Bank Failure Prediction Models for the Developing and Developed Countries: Identifying the Economic Value Added for Predicting Failure. Asian Economic and Financial Review, 6(9), 522-33. - 251