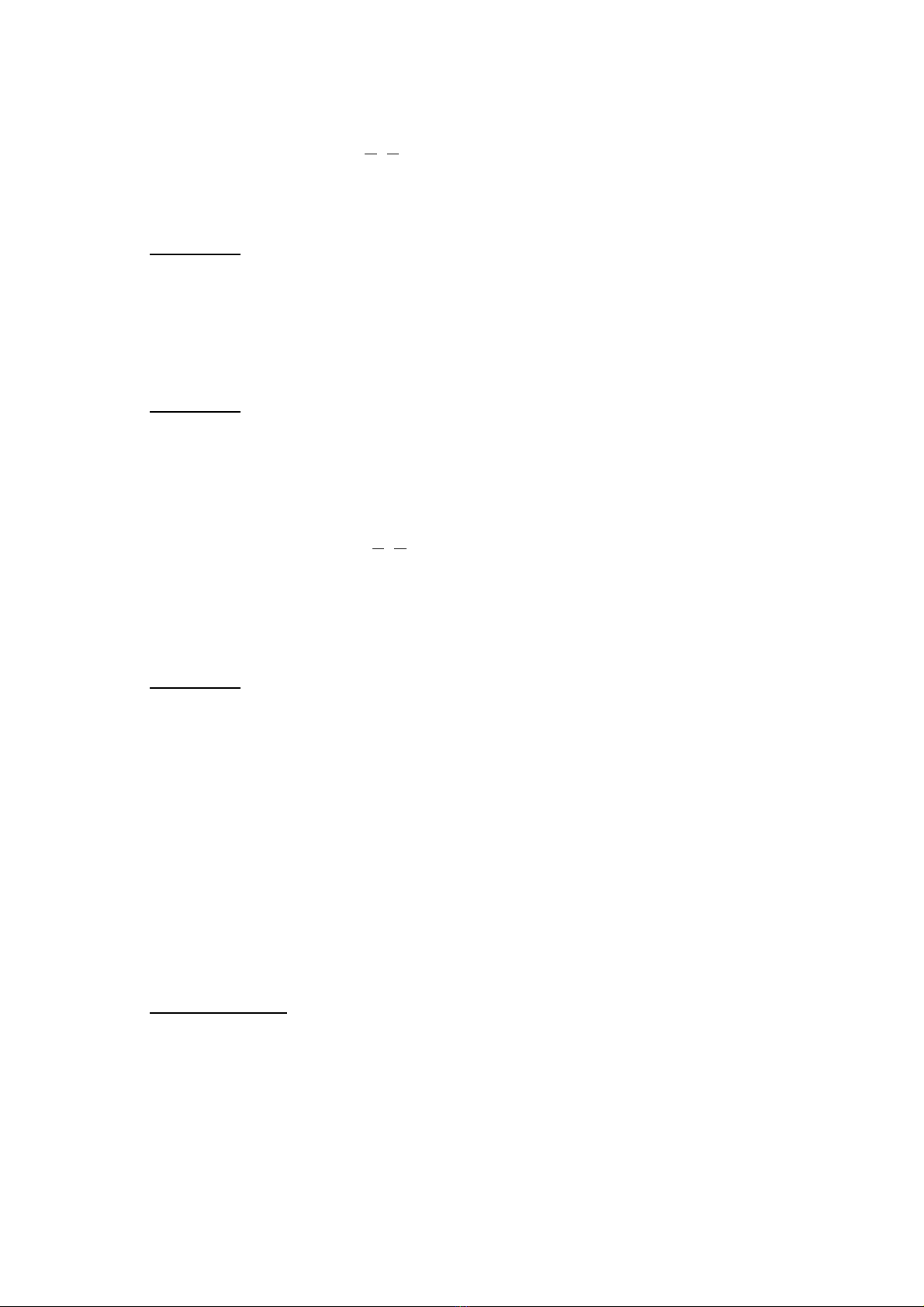Trang chủ » Tài Liệu Phổ Thông » Sáng kiến kinh nghiệm

15 trang

256 lượt xem

SKKN: Sử dụng các tính chất trong hình học phẳng để giải một số bài toán trong đề thi TN THPT quốc gia và thi HSG tỉnh Thanh Hóa

Mục tiêu của đề tài là nhằm mục đích giúp học sinh có một định hướng rõ ràng hơn khi đứng trước một bài toán phương pháp tọa độ trong mặt phẳng. Giúp các em học sinh biết phân tích, liên hệ giữa tích chất của một số hình và yêu cầu của đề bài, từ đó xây dựng lời giải.

Chủ đề:

thuyanlac888

Sáng kiến kinh nghiệm lớp 12

SKKN Toán 12

“S D NG CÁC TÍNH CH T TRONG HÌNH H C PH NG Đ GI IỬ Ụ Ấ Ọ Ẳ Ể Ả

M T S BÀI TOÁN TRONG Đ THI TN THPT QU C GIA VÀ THIỘ Ố Ề Ố

HSG T NH THANH HÓA”Ỉ

1. M ĐUỞ Ầ

1.1. Lý do ch n đ tài.ọ ề

Trong c u trúc c a đ thi TN THPT qu c gia và thi HSG c p t nh, bài ấ ủ ề ố ấ ỉ

toán ph ng pháp t a đ trong m t ph ng là m t bài toán khó, yêu c u ph i ươ ọ ộ ặ ẳ ộ ầ ả

là h c sinh khá, gi i n m v ng ki n th c v hình h c ph ng và có k năng ọ ỏ ắ ữ ế ứ ề ọ ẳ ỹ

v n d ng ki n th c linh ho t thì m i có th làm đc bài toán này.ậ ụ ế ứ ạ ớ ể ượ

Nh ng năm g n đây, vi c khai thác các tính ch t c a hình h c ph ng đữ ầ ệ ấ ủ ọ ẳ ể

đa vào bài toán ph ng pháp t a đ trong m t ph ng th ng đc ng i raư ươ ọ ộ ặ ẳ ườ ượ ườ

đ quan tâm. Do đó, h c sinh mu n gi i đc nh ng bài toán này thì giáo ề ọ ố ả ượ ữ

viên ph i yêu c u h c sinh n m v ng các ki n th c c a hình h c ph ng, đcả ầ ọ ắ ữ ế ứ ủ ọ ẳ ặ

bi t là các tính ch t c a các hình. Vi c này r t quan tr ng trong quá trình ti pệ ấ ủ ệ ấ ọ ế

c n và gi i quy t các bài toán ph ng pháp t a đ trong m t ph ng.ậ ả ế ươ ọ ộ ặ ẳ

1.2. M c đích nghiên c u.ụ ứ

Tôi ch n đ tài này nh m m c đích giúp h c sinh có m t đnh h ng ọ ề ằ ụ ọ ộ ị ướ

rõ ràng h n khi đng tr c m t bài toán ph ng pháp t a đ trong m t ơ ứ ướ ộ ươ ọ ộ ặ

ph ng. Giúp các em h c sinh bi t phân tich, liên h gi a tích ch t c a m t sẳ ọ ế ệ ữ ấ ủ ộ ố

hình và yêu c u c a đ bài, t đó xây d ng l i gi i.ầ ủ ề ừ ự ờ ả

1.3. Đi t ng nghiên c u.ố ượ ứ

Tính ch t c a các hình ph ng r t nhi u, khuôn kh c a đ tài l i có ấ ủ ẳ ấ ề ổ ủ ề ạ

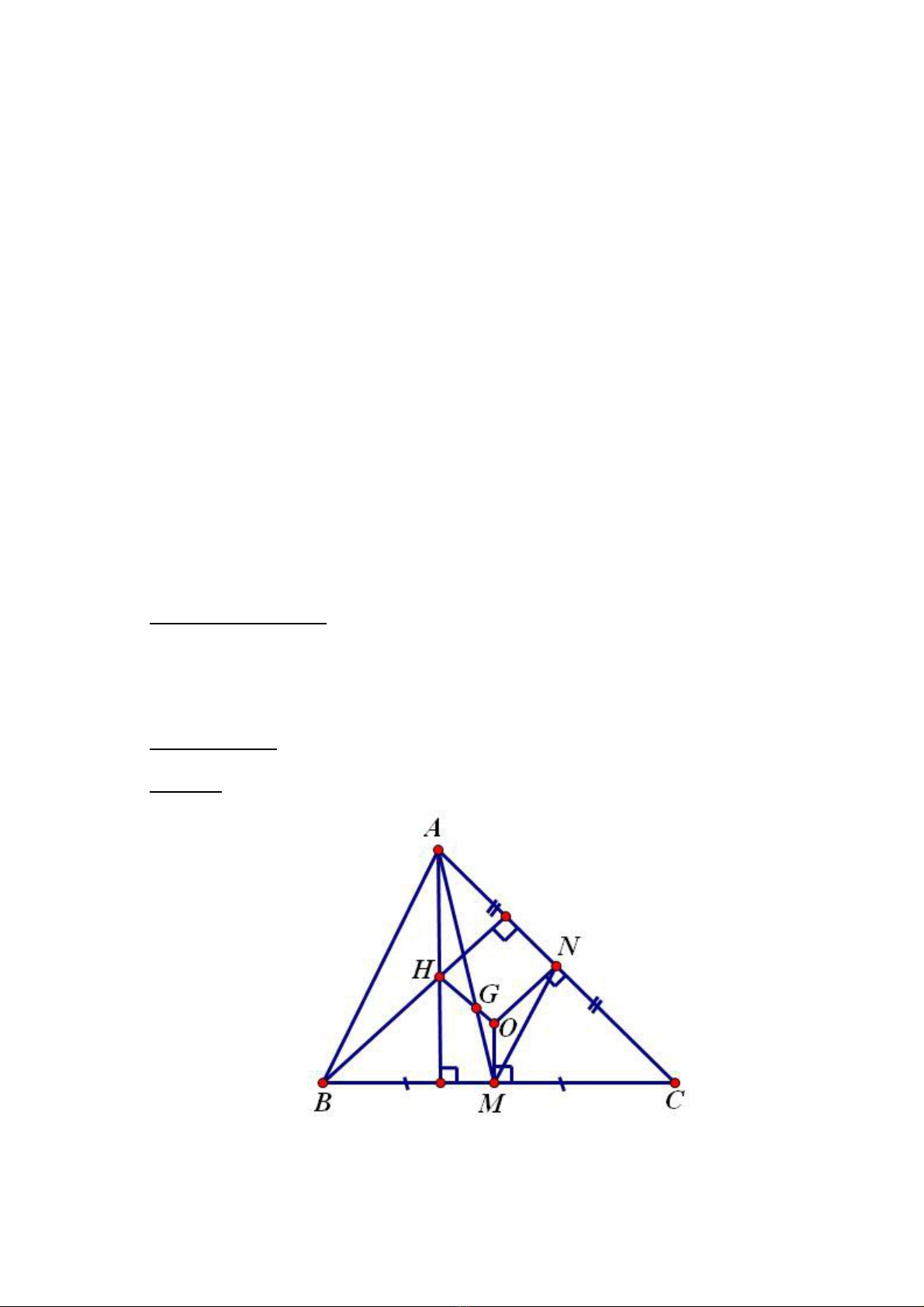
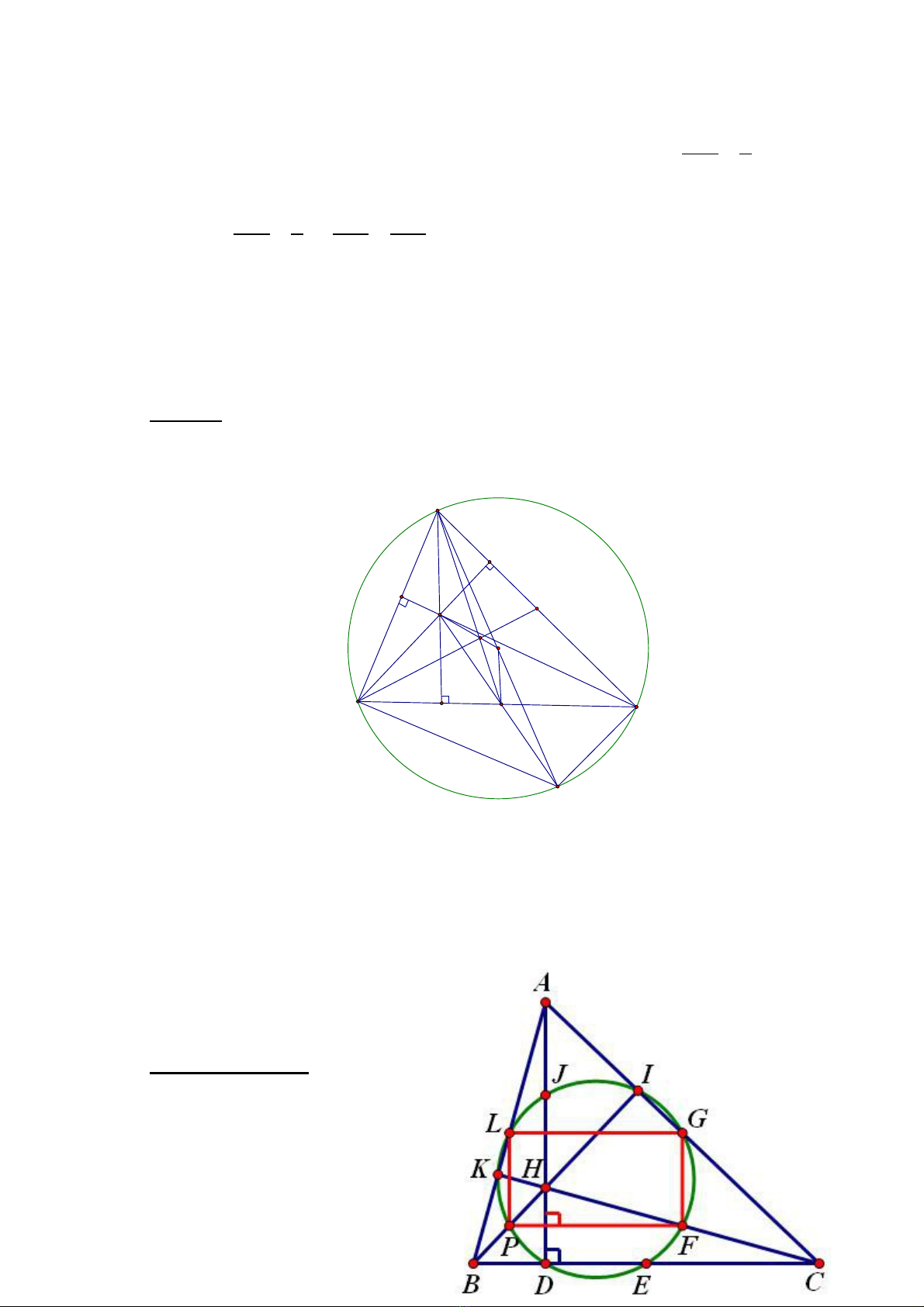
h n, nên đây tôi xin đc trình bày hai tính ch t quan tr ng c a các đi m ạ ở ượ ấ ọ ủ ể

đc bi t trong m t tam giác, đó là: Đng th ng -le và đng tròn -le.ặ ệ ộ ườ ẳ Ơ ườ Ơ

trong ch ng trình hình h c ph thông, trong sách giáo khoa không Ở ươ ọ ổ

tr c ti p gi i thi u các tính ch t này nh nh ng đnh lý thông d ng, vì v y ự ế ớ ệ ấ ư ữ ị ụ ậ

khi s d ng vào bài gi i c a mình, b t bu c h c sinh ph i ch ng minh. ử ụ ả ủ ắ ộ ọ ả ứ

Đng nhiên , vi c ch ng minh nh ng tính ch t này cũng không qua ph c ươ ệ ứ ữ ấ ứ

t p.ạ

1.4. Ph ng pháp nghiên c u.ươ ứ

D a trên s phân tích và phân lo i bài toán, đi chi u v i các tính ch tự ự ạ ố ế ớ ấ

c a hình ph ng, t đó tìm ra s liên quan. K t h p v i ph ng pháp quy n p ủ ẳ ừ ự ế ợ ớ ươ ạ

chúng ta s có đc nh ng chuyên đ h u ích, nh ng chìa khóa quan tr ng cóẽ ượ ữ ề ữ ữ ọ

th gi i quy t đc các bài toán khó. T đó hình thành l i t duy khoa h c ể ả ế ượ ừ ố ư ọ

sáng t o, có th n y sinh nhi u ý t ng phong phú, xây d ng đc nhi u bài ạ ể ả ề ưở ự ượ ề

toán hay giúp ích cho quá trình h c và ôn t p ki n th c đ có k t qu cao ọ ậ ế ứ ể ế ả

trong các k thi.ỳ

2. N I DUNG SÁNG KI N KINH NGHI MỘ Ế Ệ

2.1. C s lí lu n c a sáng ki n kinh nghi m.ơ ở ậ ủ ế ệ

Tôi xin nh c l i hai tính ch t có liên quan t i bài vi t này, đng th i cũngắ ạ ấ ớ ế ồ ờ

đ xu t cách ch ng minh t ng ng (Đng nhiên cũng s có nh ng cách ề ấ ứ ươ ứ ươ ẽ ữ

khác đ ch ng minh hai tính ch t này). ể ứ ấ

Đng th ng -leườ ẳ Ơ :Trong tam giác, tâm đng tròn ngo i ti p I, tr c tâm ườ ạ ế ự

H, tr ng tâm G th ng hàng. Đng th ng đi qua 3 đi m th ng hàng nói ọ ẳ ườ ẳ ể ẳ

trên g i là đng th ng -le.ọ ườ ẳ Ơ

Ch ng minh:ứ

Cách 1: S d ng tam giác đng d ngử ụ ồ ạ

Hình v 1ẽ

Các đi m đc đt nh trên hình vể ượ ặ ư ẽ

D dàng ch raễ ỉ : ∆HAB đng d ng v iồ ạ ớ ∆OMN (g.g)

=�

L i có : ạ

GM GM OM

GA GA AH

= =�

,m t khác : ặ

ﾷ

HAG GMO=

suy ra ∆AHG đng d ng v iồ ạ ớ ∆MOG

ﾷ

AGH MGO=�

nên H, G, O th ng ẳ

hàng.

Cách 2: V đng kính AD. ( Cách ch ng minh này khá đn gi n, xin phép ẽ ườ ứ ơ ả

cho tôi không trình bày đây)ở

Hình v 2ẽ

Qua ch ng minh trên ta d dàng suy ra đc:ứ ễ ượ

1, T giác BHCD là hình bình hành.ứ

2AH IM

uuur uuur

3IH IG

uuur uur

Đng tròn -leườ Ơ : Trong m t tam giác, chân 3 đng cao, 3 trung đi m 3 ộ ườ ể

c nh và 3 trung đi m các đo n th ng n i tr c tâm đn đnh cùng n m ạ ể ạ ẳ ố ự ế ỉ ằ

trên m t đng trònộ ườ .

Ch ng minh:ứ
Đt tên các đi m nh  hình v .ặ ể ư ẽ
Hình v  3ẽ
Đ ý th yể ấ    là hình ch  nh t nên n i ti p đng tròn có tâm là trung ữ ậ ộ ế ườ
đi m c aể ủ    và  . 
T ng t :ươ ự
 là hình ch  nh t nên n i ti p đng tròn có tâm là trung đi m c aữ ậ ộ ế ườ ể ủ  
và   
 là hình ch  nh t nên n i ti p đng tròn có tâm là trung đi m c aữ ậ ộ ế ườ ể ủ    
và   
 là hình ch  nh t nên n i ti p đng tròn có tâm là trung đi m c aữ ậ ộ ế ườ ể ủ    
và   
T   (1), (2), (3), (4)ừ  suy ra   đi mể  D, E, F, G, I, J, L, K, P  n m trên ằ
cùng m tộ đng tròn (đng tròn 9 đi m - đng tròn  -le).ườ ườ ể ườ Ơ  
2.2. Th c tr ng v n đ tr c khi áp d ng sáng ki n kinh nghi m.ự ạ ấ ề ướ ụ ế ệ
        Tôi xin nêu ra 5 bài toán mà n u gi i nó theo cách không s  d ng hai tínhế ả ử ụ  
ch t nêu trên thì bài toán s  tr  nên dài dòng, ph c t p (đi u này đã đc ấ ẽ ở ứ ạ ề ượ
ki m tra th c t  trên các ti t d y b i d ng ki n th c trên l p h c).ể ự ế ế ạ ồ ưỡ ế ứ ớ ọ
Bài toán 1:
         Trong m t ph ng t a đ Oxy, cho tam giác ABC có tr c tâm H(-1;4), ặ ẳ ọ ộ ự
tâm đng tròn ngo i ti p I(-3;0) và trung đi m c nh BC là đi m M(0;-3). ườ ạ ế ể ạ ể
Tìm t a đ các đnh c a tam giác.ọ ộ ỉ ủ
Bài toán 2:
4