1
Phương Phương phápháp p giảgiải i mã mã
vòvòng Meggittng Meggitt
Giáo viên thực hiện: Lê Thị Thanh
Định lý Meggitt
•Giả sử s(x) là syndrome của:
• u(x) = u0xn-1 + u1xn-2 + ... + un-2x + un-1 thì syndrome
của u1(x) là s1(x) được tính theo công thức sau:
• s1(x) = xs(x) mod g(x)
Chứng minh định lý Meggitt
• Với quy ước u1(x) là quay vòng trái của u(x).
• u(x) = u0xn-1 + u1xn-2 + ... + un-2x + un-1
• u1(x) = u1xn-1 + u2xn-2 + ... + un-1x + u0
• u1(x) mod g(x) = xs(x) mod g(x) =
• = x. (u(x) mod g(x)) mod g(x)
•u1(x) mod g(x) = x.u(x) mod g(x)
• (u1xn-1 + u2xn-2 + ... + un-1x + u0) mod g(x) =
• = (u0xn+ u1xn-1 + ... + un-2x2+ un-1x) mod
g(x)
• => u0(xn+ 1) mod g(x) = 0
6.4 Khả năng sửa sai của bộ mã vòng (n,k)
•6.4.1 Độ dài sai
•6.4.2 Khả năng dò sai
•6.4.3 Xác suất không dò được sai của các
mẫu sai
•6.4.4 Xác suất không dò được sai của bộ
mã vòng
2
6.4.1 Độ dài sai
•Độ dài sai: Giả sử e = e0e1... en-1=
• = (e0e1... ei-1 ei ei+1 ... ej-1 ej ej+1 ...en-1)
• = (00 ... 0 1 ei+1 ... ej-11 00 ... 0)
•Khi đó độ dài sai được định nghĩa là khoảng
cách từ bit ei tới bit ej:
• độ dài sai = j – i + 1
•Độ dài sai vòng: giả sử e = e0e1... en-1=
• = (e0e1... ei-1 ei ei+1 ... ej-1 ej ej+1 ...en-1)
• = (e0e1... ei-1 1 0 0... 0 1 ej+1 ...en-1)
•Độ dài sai vòng được định nghĩa là khoảng
cách vòng từ bit ei đến bit ej.
• độ dài sai vòng = n – (j – 1 – i – 1 + 1) =
• = n – j + i + 1)
6.4.2 Khả năng dò sai (1/3)
•Định lý 6.7: Bộ mã vòng (n,k) có thể dò
được tất cả các mẫu sai nhỏ hơn hoặc bằng
(n-k) bit. (kể cả độ dài sai vòng).
•Chứng minh:
•Bổ đề: “Nếu bộ mã vòng (n,k) có khả năng
phát hiện được đa thức gây sai e(x) thì sẽ
phát hiện được tất cả các đa thức gây sai
ei(x) là đa thức dịch chuyển vòng i bit của
e(x) (i=1,n-1)”.
6.4.2 Khả năng dò sai (2/3)
• Giả sử ei(x) là đa thức gây sai không phát
hiện được →ei(x) cũng là đa thức mã (mâu
thuẫn). Do đó ta chỉ cần chứng minh định lý
với độ dài sai tuyệt đối.
•Giả sử e(x) = E(x).xi với 0 ≤ i ≤ n-1 → vector
sai ứng với E(x) có độ dài ≤ (n-k) → bậc của
E(x) ≤ (n-k-1)
•Để phát hiện được sai trong mã vòng thì
phải chứng minh rằng e(x) không phải từ
mã, tức là e(x) không chia hết cho g(x).
3
6.4.2 Khả năng dò sai (3/3)
•Nhận xét: E(x) có bậc nhỏ hơn g(x); E(x) # 0
→ E(x) không chia hết cho g(x).
•Mặt khác, vì hệ số tự do của g(x) là khác
không nên xi sẽ không chức một thừa số
nào của g(x). Vậy E(x).xi sẽ không chia hết
cho g(x).
•Vậy đa thức sai e(x) là dò được.
6.4.3 Xác suất không dò được sai
•Định lý 6.8: ”Xác suất không dò được các
mẫu sai có độ dài bằng (n-k+1) là 2-(n-k-1)”.
•Chứng minh: e(x) = E(x).xi
•E(x) có n-k+1 số hạng → E(x) có bậc n-k.
•Khi không phát hiện được sai thì E(x) là đa
thức mã có bậc n-k, mà đa thức mã bậc n-k
duy nhất là g(x).
6.4.3 Xác suất không dò được sai
•Có 2(n-k-1) đa thức nhưng chỉ có một đa thức
E(x) = g(x) làm cho sai e(x) là không dò
được. Vậy xác suất không dò được sai của
các mẫu sai có độ dài bằng (n-k+1) là:
• Pud = 1/ 2(n-k-1) = 2-(n-k-1)
6.4.4 Định lý 6.9
•Định lý 6.9: xác suất không dò được sai của
bộ mã vòng (n,k) là 2(k-n).
•Chứng minh:
•Số đa thức gây sai: 2n– 1
•Số đa thức mã khác không: 2k– 1
•Vậy xác xuất không dò được sai là:
• Pud = 2k– 1 / 2n– 1 = 2k-n
4
Phương pháp giải mã vòng Meggitt
•Nguyên lý giải mã
•Thiết kế mạch thực hiện giải mã
Nguyên lý giải mã Meggitt
•Phương pháp này sửa sai cho tất cả các
mẫu sai 1 bit
•Giả sử nhận được đa thức:
u(x)=u0xn-1+u1xn-2+...+un-1
•Chọn một mẫu sai có thể sửa sai được
e(x)=e0xn-1+e1xn-2+...+en-1 với e0=1
•So sánh syndrome của u(x) và syndrome
của e(x):
–Không khớp: tính syndrome của u(1)(x) từ
syndrome của u(x)
–Khớp: sửa sai và tính syndrome của
u’
(1)
(
x
)
t
ừ
syndrome
a u(x)
Syndrome của u(x) không bằng syndrome
của e(x)
•Quay vòng
u(x)=u0xn-1+u1xn-2+...+un-1 để được
u(1)(x)=u1xn-1+u2xn-2+...un-1x+u0
Do u0xn+u0=u0(xn+1) chia hết cho g(x) nên:
s(1)(x) =dư số[u(1)(x)/g(x)]
=dư số[(u(1)(x)+u0xn+u0)/g(x)]
=dư số[(u0xn+u(1)(x)+u0)/g(x)]
=dư số[(u0xn+u1xn-1+u2xn-2+...+un-1x+u0+u0)/g(x)]
Syndrome của u(x) không bằng syndrome
của e(x)
•Quay vòng
u(x)=u0xn-1+u1xn-2+...+un-1 để được
u(1)(x)=u1xn-1+u2xn-2+...un-1x+u0
Do u0xn+u0=u0(xn+1) chia hết cho g(x) nên:
s(1)(x)=dư số[u(1)(x)/g(x)]
=dư số[(u(1)(x)+u0xn+u0)/g(x)]
=dư số[(u0xn+u(1)(x)+u0)/g(x)]
=dư số[(u0xn+u1xn-1+u2xn-2+...+un-
1x+u0+u0)/g(x)]
=dư số[(xu(x)+0)/g(x)]
=dư số[xu(x)/g(x)]
=dư số[x(kg(x)+dư số[u(x)/g(x)])/g(x)]
5
Syndrome của u(x) không bằng syndrome
của e(x)
=dư số[x(kg(x)+dư số[u(x)/g(x)])/g(x)]
=dư số[x(kg(x)+s(x)])/g(x)]
=dư số[xkg(x)/g(x)+dư số[xs(x)/g(x)]
=0+dư số[xs(x)/g(x)]
=dư số[xs(x)/g(x)]
•Do đó khi đã có syndrome của u(x) là s(x) thì có
thể tính syndrome s(1)(x) của u(1)(x) bằng cách dịch
trái s(x)
Syndrome của u(x) bằng syndrome của
e(x)
•Sửa sai bit đầu tiên:
u(x) sửa sai bit đầu (cộng với e0=1) được u’(x)
u’(x)=(u0+e0)xn-1+u1xn-2+...+un-1=u(x)+e0xn-1
Lúc đó syndrome của u’(x) là:
s’(x) =dư số[u’(x)/g(x)]=dư số[(u(x)+e0xn-1)/g(x)]
=dư số[u(x)/g(x)]+dư số[xn-1/g(x)]
=s(x)+dư số[xn-1/g(x)]
Syndrome của u(x) bằng syndrome của
e(x)
•Quay vòng trái u’(x) và tính syndrome của nó:
u’(1)(x)=u1xn-1+u2xn-2+...+un-1x+(u0+e0)=u(1)(x)+e0
s’(1)(x) =dư số[u’(1)(x)/g(x)]
=dư số[(u(1)(x)+e0)/g(x)]
=dư số[(u(1)(x)/g(x)]+dư số[e0/g(x)]
=dư số[xs(x)/g(x)]+dư số[e0/g(x)]
=dư số[(xs(x)+e0)/g(x)]
•Do đó khi đã có syndrome của u(x) là s(x) thì có thể tính
syndrome s’(1)(x) của u’(1)(x) bằng cách dịch trái s(x) và
cộng thêm e0 vào bit trọng số thấp nhất
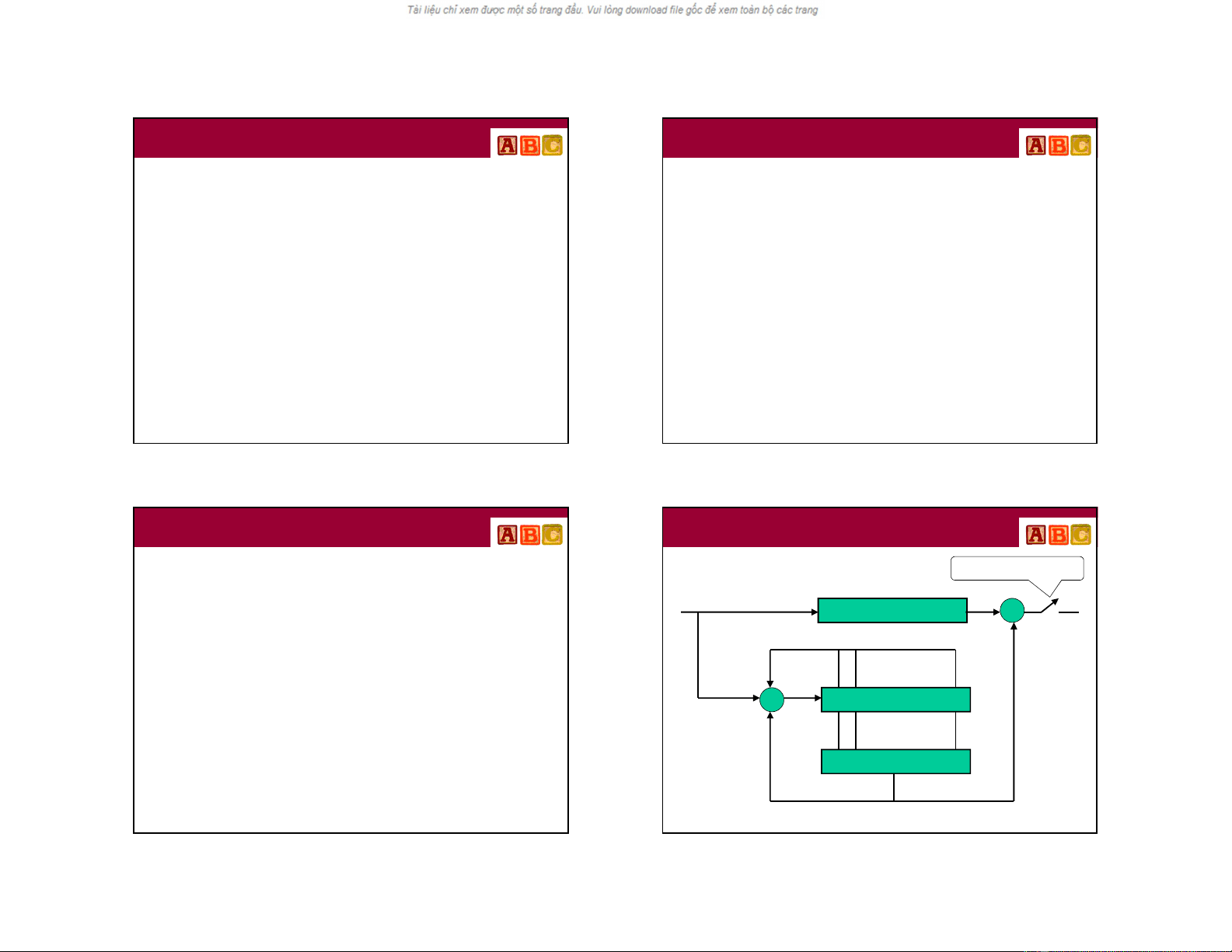
Thiết kế mạch giải mã Meggitt
Thanh ghi syndrome
So sánh mẫu sai
Bộ đệm
+
+
u(x)
1: khớp, 0: không khớp
Đóng từ xung n