Tuaàn : 9 , 10 ChuongI : §4 Bài 4 : THỂ TÍCH KHỐI ĐA DIỆN
Ngày 9/10/2008 (Chương trình nâng cao)
Tiết:9 ; 10
Lớp12A1
I. Mục tiêu:
1.Về kiến thức:
Làm cho hs hiểu được khái niệm thể tích của khối đa diện,các công thức tính thể tích của một số khối đa diện
đơn giản.
2.Về kỹ năng:
Vận dụng được kiến thức để tính thể tích của các khối đa diện phức tạp hơn và giải một số bài toán hình học.
3.Về tư duy-thái độ:
- Rèn luyện tư duy logic,biết quy lạ về quen.
- Thái độ cần cù,cẩn thận,chính xác.
II. Chuẩn bị của giáo viên và học sinh
1.Giáo viên:giáo án,bảng phụ,phán màu,phiếu học tập
2.Học sinh:sgk,thước kẻ
Kiến thức đã học:khái niệm khối đa diện,khối chóp,khối hộp chữ nhật,khối lập phương
III. Tiến trình bài học:
1.Ốn định lớp:điểm danh sĩ số
2.Kiểm tra bài cũ:
Câu hỏi 1:Nêu các định nghĩa :Hai khối đa diện bằng nhau,hai hình lập phương bằng nhau,bát diện đều.
Câu hỏi 2:Cho 1 khối hộp chữ nhật với 3 kích thước 2cm,5cm,7cm.Bằng những mặt phẳng song song với các
mặt của khối hộp có thể chia được bao nhiêu khối lập phương có cạnh bằng 1cm?
3.Bài mới:
Hoạt động 1: Hình thành khái niệm thể tích của khối đa diện
HĐ của giáo viên HĐ của học sinh
Dẫn dắt khái niệm thể tích từ khái niệm diện tích của đa
giác
1.Thế nào là thể tích của một khối đa diện?
Khái niệm:Thể tích của khối đa diện là số đo của phần
không gian mà nó chiếm chỗ
Liên hệ với kt bài cũ nêu tính chất
Tính chất: SGK
Chú ý : SGK
Nắm khái niệm và tính chất của thể tích khối đa
diện
Hoạt động 2: Thể tích của khối hộp chữ nhật
HĐ của giáo viên HĐ của học sinh
Từ câu hỏi 2 của kt bài cũ,hỏi tt cho khối hộp chữ nhật
với ba kích thước a,b,c
H: Từ đó ta có thể tích của khối hộp bằng bao nhiêu?
2.Thể tích của khối hộp chữ nhật
Định lý 1: SGK
V = a.b.c
H:Khi a = b = c ,khối hộp chữ nhật trở thành khối Chú
ý:Thể tích của khối lập phương cạnh a bằng a3
V = a3
Hs trả lời : a.b.c
Hs trả lời :a.b.c
gì?Thể tích bằng bao nhiêu?
Nêu chú ý
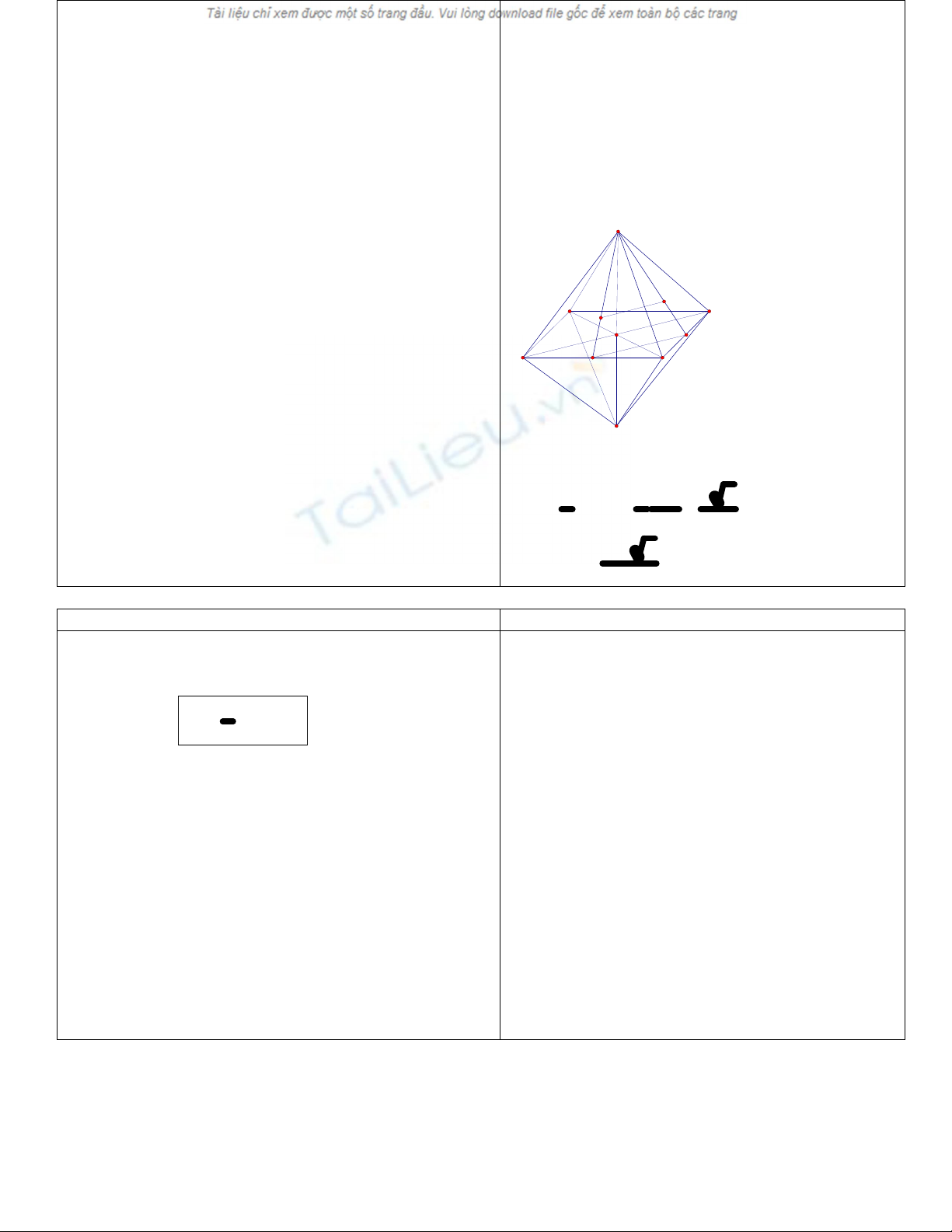
Ví dụ 1:Tính thể tích của khối lập phương có các đỉnh là
trọng tâm các mặt của một khối tám mặt đều cạnh a.
Giải: SGK
H:Muốn tính thể tích khối lập phương,ta càn xác định
những yếu tố nào?
Yêu cầu hs tính MN
Yêu cầu hs về nhà cm khối đa diện có các đỉnh là trọng
tâm trong ví dụ là khối lập phương
(xem như bt về nhà)
Gọi hs đứng tại chỗ trình bày ý tưởng của bài giải trong
câu hỏi 1 sgk
(lưu ý :quy về cách tính thể tích khối hộp chữ nhật)
Hs trả lời :Độ dài của một cạnh
Hs trả lời
D
B
N
N'
M'
S'
S
C
A
H
27
22
3
2
23
2
''
3
2
3
3a
MNV
aAC
NMMN
==
===
Hoạt động 3 : Thể tích của khối chóp
HĐ của giáo viên HĐ của học sinh
3.Thể tích của khối chóp
Định lý 2: SGK
V =
3
1S .h
Ví dụ 2:Cho hình chóp tứ giác đều SABCD cạnh đáy
bằng a,cạnh bên bằng b.O là giao điểm của AC và BD
a)Tính thể tích V1 của khối đa diện SABCD
b)Cho a = b,gọi S là giao điểm đối xứng với S qua
O.Tính thể tích V của khối đa diện S’SABCD
SABCD = a2
D
B
0
S'
S
C
A
Gọi hs lên bảng trình bày
Khuyến khích học sinh giải bằng nhiều cách khác nhau
Nhận xét,hoàn thiện
2
2
2
22
a
b
AOSASO
−=
−=
222
1
24
6
1
.
3
1
aba
SOSV ABCD
−=
=
Khi a = b
6
2
3
1a
V=
3
2
3
1a
VV ==
4. Cuõng coá :
- Coâng thöùc tính theå tích khoái hoäp cn , khoái laäp phöông , khoái choùp
- Phöông phaùp tính
Tiết 2:
1 . oån ñònh lôùp :
2 . Kieåm tra baøi cuõ : caùc coâng thöùctính theå tích
3 . Baøi môùi :
Hoạt động 1 : Thể tích của khối lăng trụ
HĐ của giáo viên HĐ của học sinh
4.Thể tích của khối lăng trụ:
Bài toán:SGK
B'
C'
A'
C
B
A
Triển khai bài toán,yêu cầu hs làm bài toán theo gợi ý 3
bước trong SGK
Gv sử dụng mô hình 3 khối tứ diện ghép thành khối lăng
trụ tam giác trong bài toán
Yêu cầu hs thiết lập công thức của khối lăng trụ đứng
Dẫn dắt từ ví dụ hình 30 nêu định lý 3
Định lý 3: SGK
Hs nhận xét hình 30,phát biểu kết luận
Nêu cách tính thể tích của khối lăng trụ đứng
Giải:
a)BA’B’C’,A’BCC’,A’ABC
b)Ba khối tứ diện có các chiều cao và diện tích đáy
tương ứng bằng nhau nên co thể tich bằng nhau
c) hShSVV ABCABCABCA ..
3
1
.33 '===
V = S .h
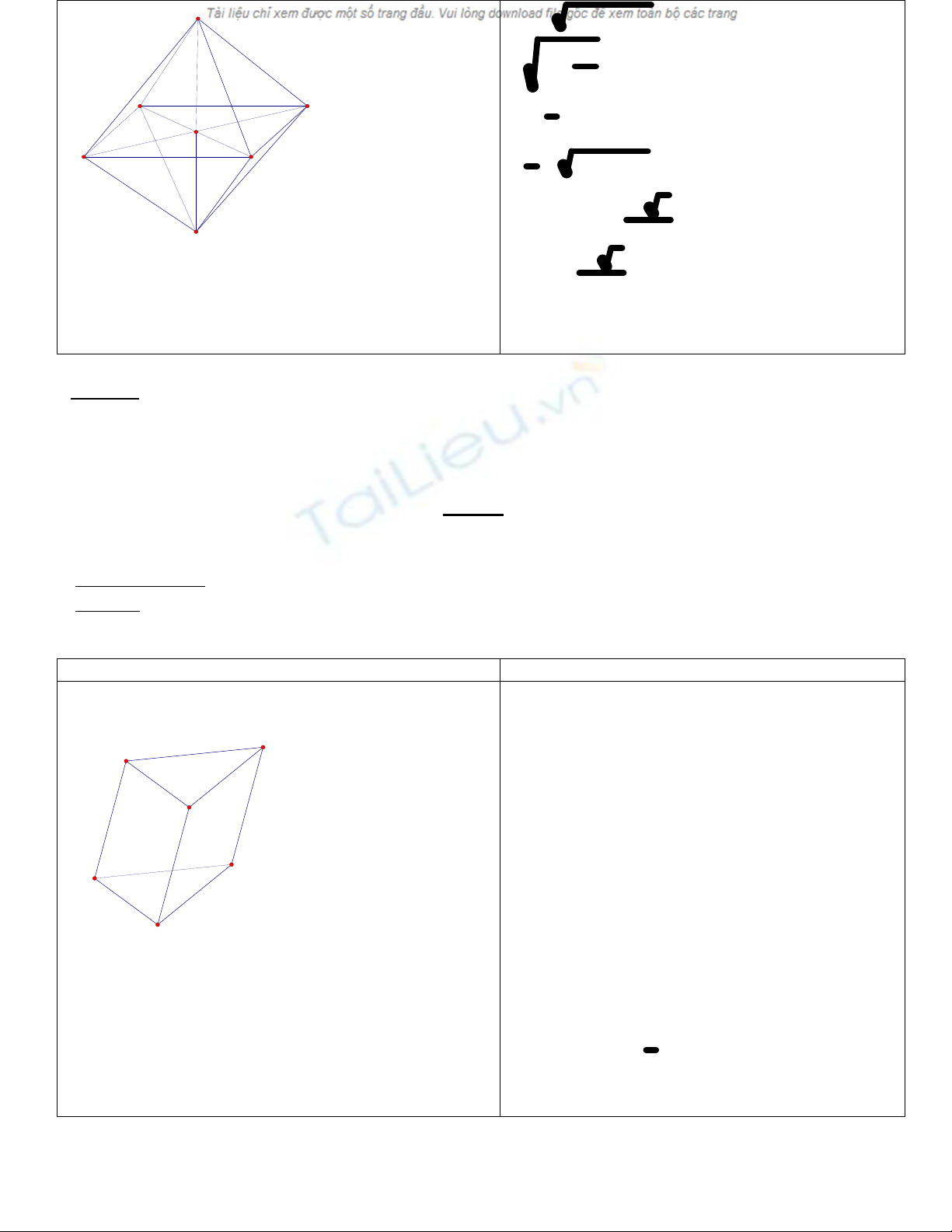
Ví dụ 3:Cho khối lăng trụ ABC.A’B’C’.Gọi M’,N’ lần
lượt là trung điểm của hai cạnh AA’ và BB’.Mặt phẳng
(MNC) chia khối lăng trụ đã cho thành hai phần.Tính tỉ
số thể tích của hai phần đó.
N
B'
A'
C'
A
B
C
M
Gọi hs lên bảng trình bày
Nhận xét,chỉnh sửa
Cách 2: Gọi P là trung điểm của CC’ ,yêu cầu hs về nhà
cm bài toán này bằng cách 2
Gọi V là thể tích khối lăng trụ
VV
VV
BCABA
CBCA
3
2
3
1
''
'''
=⇒
=
''BCMNACMNAB VV =
VVCABMN
3
1
=⇒
2
1
'''
=
CBCMNA
CABNM
V
V
Hoạt động 2 : Bài tập củng cố
HĐ của giáo viên HĐ của học sinh
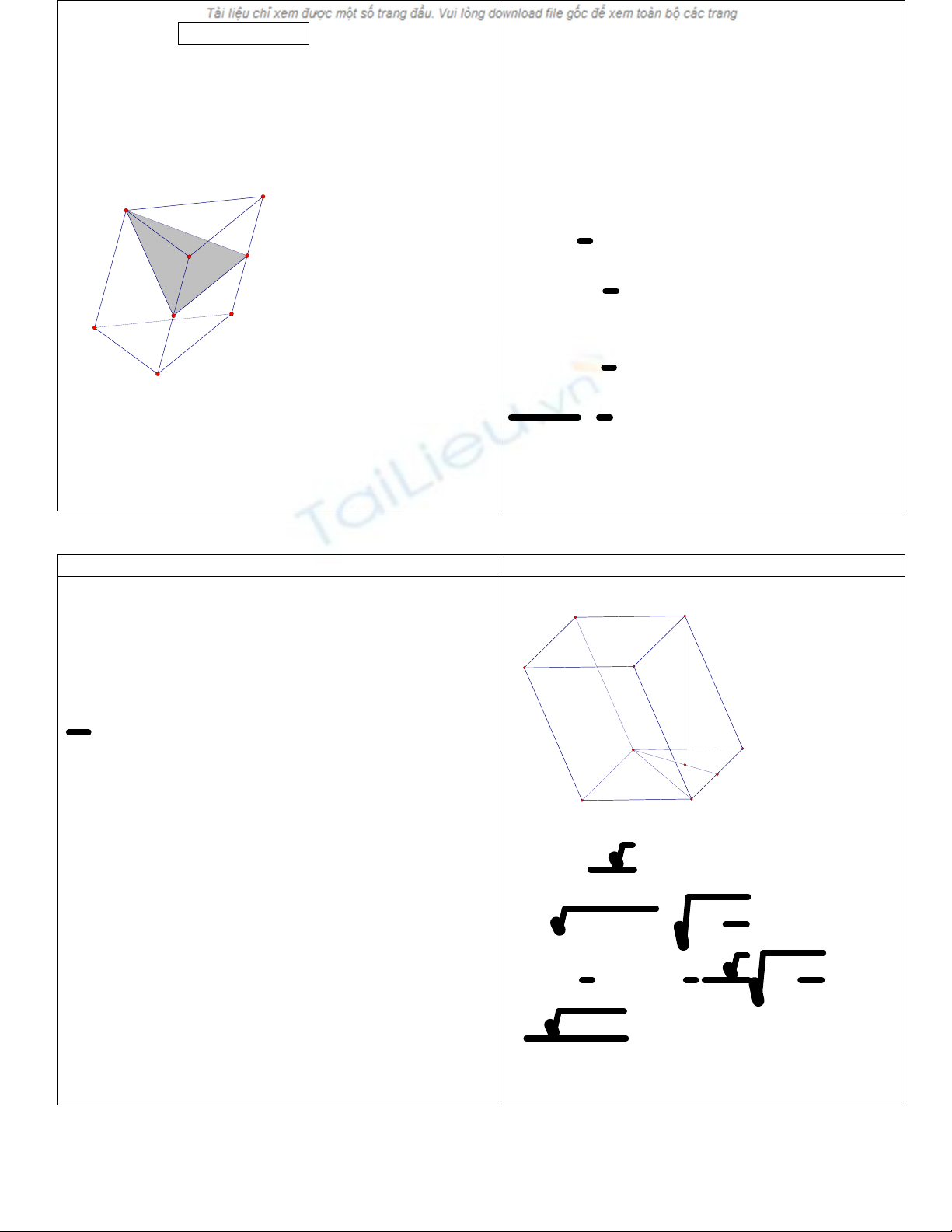
Bài toán: Cho khối hộp ABCD.A’B’C’D’ có đáy là hình
thoi cạnh a,A’C’ = a,độ dài cạnh bên bằng b.Đỉnh D
cách đều 3 đỉnh A’,D’,C’
a)Tính thể tích khối tứ diện DA’C’D’,tính thể tích V của
khối hộp
b)Gọi V1 là thể tích của khối đa diện ABCDA’C’.Tính
V
V1
Yêu cầu hs xác định đường cao của hình chóp DA’D’C’
Gọi hs lên bảng trình bày câu a
Gợi ý :Tính tỉ số thể tích giữa VDA’C’D’ và V ?
a
b
a
a
M
ID'
C'
B'
A'
D
C
B
A
a)
4
3
2
''' a
SCDA =.
3
'' 2
222 a
bIDDDDI −=−=
12
3
34
3
.
3
1
.
3
1
222
2
2
2
''''''
aba
a
b
a
SDIV CDACDDA
−
=
−==
Gọi hs lên bảng làm câu b
Nhận xét,chỉnh sửa
2
3
6222
''' aba
VV CDDA −
== .
b) .
6
1
''' VV CBBA =
VVVVVVVV DCDACBBA
3
2
6
1
6
1
''''''1 =−−=−−=
3
2
1=⇒
V
V
4. Củng cố:
- Củng cố lại các công thức tính thể tích khối đa diện
5. Daën doø ;
- Làm các bài tập trong SGK và sách bài tập
6 . Ruùt kinh nghieäm :