Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 31 Löu Tuaán Hieäp
PHỤ LỤC ĐÁP SỐ
Phần I
1.1.
3
3
a
1.2.
3
6
6
a
1.3.
3
3
12
a
1.4.
3
2 2
3
a
1.5.
3
2 2
3
a
1.6.
3
6
3
a
1.7. 3
a
1.8.
3
2 3
9
a
1.9.
3
3
3
a
1.10.
1
4
1.11.
3
3
12
a
1.12.
3
3
6
a
1.13.
22
xq babaS
22
tq babaaS
ba
6
1
V2
ABC.S
ba
3
1
V2
ABCD.S
1.14. b).V = 3
2
6
a
c). R =
2
AC
2
2
a
1.15.
3
9
4
a
, R = OA=a 3
1.16. a). V= 3
. 3
6
a
b). R =
2 3
3
a
1.17. 10a3
1.18. V=
3
3
a
, R =
5
2
a
1.19. V =
3
3
2
a
1.20. R= 4
6a,S= 2
.3 2
a
.
V=
8
6. 3
a
1.21. R=
3
6a,S=
3
.8 2
a
V=
27
6.8 3
a
1.22. V=
4
3
3
a
1.23. V= 3
3
a, h = 2
a
Phần II
2.1.
2
70
xq
S a
,
3
175
V a
2.2. V= 24
.3
a
;
4
2.. 2
a
Sxq
2.3.
2 3
3 13 3
,
4 4
xq
a a
S V
2.4. S =
400 2
,V=
8000
3
2.5. Sxq=2
5
4
a
,V(N)=
3
12
a
2.6.
3
2
3
a
V
2.7.
3
2
3
a
V
2.8.
3
. .
1 11
2 24
S ABI S ABC
a
V V
2.9.
3
.
3
2
S ABC
a
V,
13
2
a
R
2.10.
3
.
6
S ABC
a
V
TRÖÔØNG TRUNG HOÏC PHOÅ THOÂNG LAI VUNG 2
Tổ Toán

Löu Tuaán Hieäp
Taøi lieäu löu haønh noäi boä
Naêm 2010
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 1 Löu Tuaán Hieäp
MỤC LỤC
PHẦN I . THỂ TÍCH KHỐI CHÓP – KHỐI LĂNG TRỤ
1. Thể tích khối chóp, khối lăng trụ ...................................................2-11
2. Thể Tích khối chóp, khối lăng trụ liên quan đến góc.....................12-16
3. Tỷ số thể tích................................................................................17-19
4. Diện tích mặt cầu – Thể tích khối cầu ngoại tiếp khối chóp ..........20-21
Bài tập tự rèn luyện ..........................................................................22-23
PHẦN II . MẶT TRÒN XOAY
1. Công Thức, Ví dụ ........................................................................24-26
2. Bài tập tự rèn luyện ...........................................................................27
PHẦN III . MỘT SỐ ĐỀ THI
Một đề thi học kỳ , tốt nghiệp liên quan đến thể tích. ....................................28-30
Phụ lục Đáp số. ..................................................................................................31
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 30 Löu Tuaán Hieäp
5. Đề thi TN 2009
Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA vuông
góc với mặt phẳng đáy. Biết
0
120
BAC , tính thể tích của khối chóp S.ABC theo a.
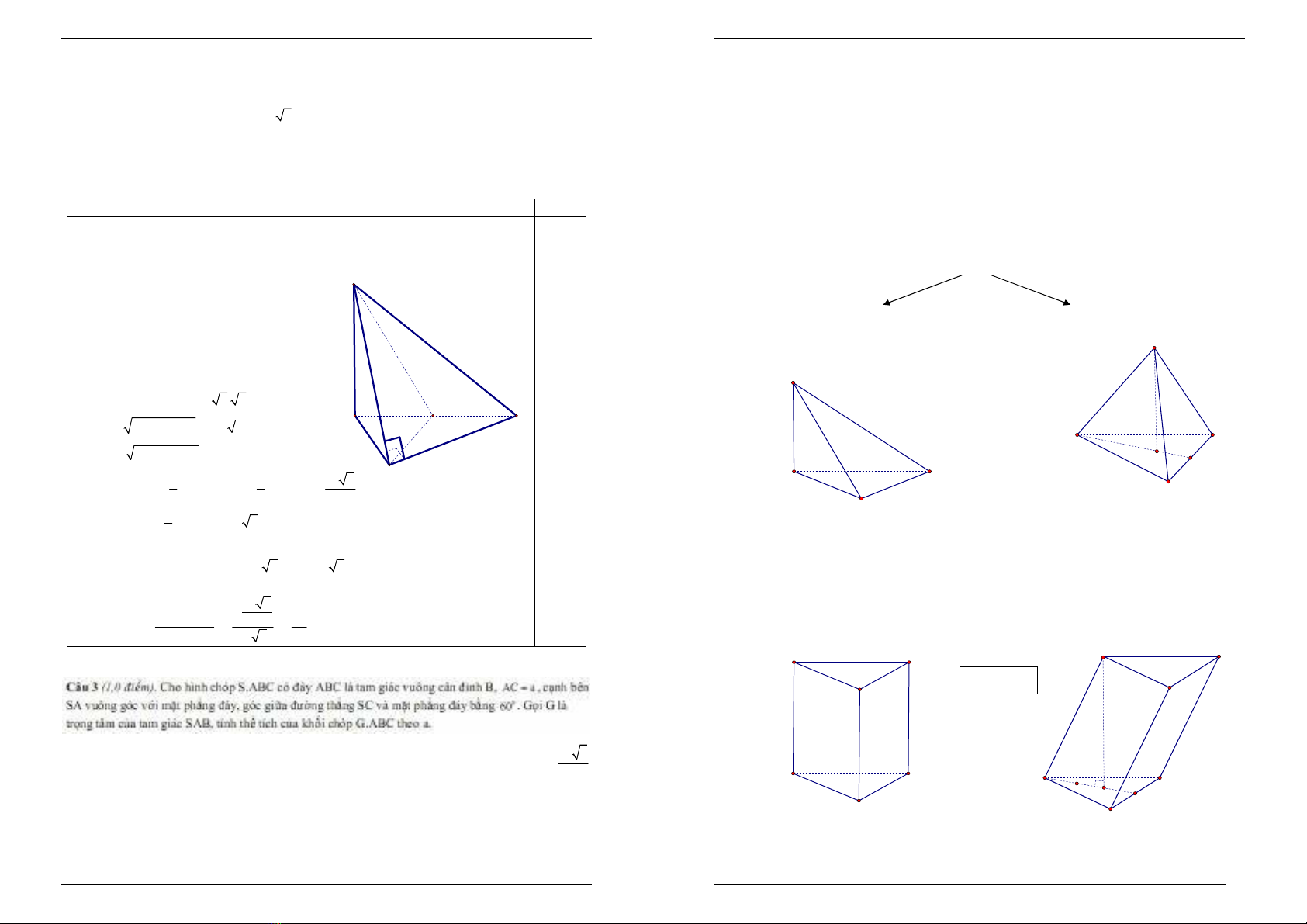
6. Đề thi TN 2010
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông
góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 600 . Tính thể
tích khối chóp S.ABCD theo a
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 29 Löu Tuaán Hieäp
3. Đề Thi Diễn Tập TN 2009. (1,0 điểm)
Cho hình chóp S.ABC có
SA
vuông góc với mặt phẳng (ABC), đáy ABC là
tam giác vuông tại B,
AB a 3, AC 2a
, góc giữa mặt bên (SBC) và mặt đáy
(ABC) bằng
0
60
. Gọi M là trung điểm của AC. Tính thể tích khối chóp S.BCM và
khoảng cách từ điểm M đến mặt phẳng (SBC).
Giải
Tính thể tích khối chóp S.BCM và khoảng cách từ điểm M đến mặt phẳng (SBC). 1.0
Do
0
SA (ABC)
BC SB SBA SBC ; ABC 60
BC AB
Xét tam giác vuông SAB và SBC ta có:
0
2 2
2 2
2
2
SA AB. tan60 a 3. 3 3a
SB SA AB 2a 3
BC AC AB a
1 1 a 3
dt( MBC) dt( ABC) AB.BC
2 4 4
1
dt( SBC) SB.BC a 3
2
Suy ra:
2 3
S.BCM
3
S.BCM
2
1 1 a 3 a 3
V dt( MBC).SA . .3a
3 3 4 4
a 3
3
3V 3a
4
d(M,(SBC))
dt( SBC) a 3 4
0.25
0.25
0.25
0.25
4. Đề Thi Diễn Tập TN 2010. (1,0 điểm)
Đáp số : 3
3
36
a
V
AC
B
S
M
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 2 Löu Tuaán Hieäp
Phaàn I. THEÅ TÍCH KHOÁI CHOÙP – KHOÁI LAÊNG TRUÏ
Trong tröôøng phoå thoâng , Hình hoïc Khoâng gian laø moät baøi toaùn raát khoù ñoái vôùi hoïc
sinh, do ñoù hoïc sinh phaûi ñoïc thaät kyõ ñeà baøi vaø töø ñoù xaùc ñònh giaû thuyeát baøi toaùn, veõ hình
roài tieán haønh giaûi baøi toaùn.
Cả hai chương trình chuẩn vaø naâng cao đều đề cập đến theå tích cuûa khoái ña dieän (
theå tích khoái choùp, khoái laêng truï).
Thoâng thöôøng baøi toaùn veà hình choùp ñöôïc phaân thaønh 2 daïng nhö sau:
Cho hình choùp
Hình choùp coù caïnh beân vuoâng goùc vôùi maët
phaúng ñaùy
AC
B
S
Ña giaùc ñaùy :
Tam giaùc vuoâng
Tam giaùc caân
Tam giaùc ñeàu
Hình vuoâng, chöõ nhaät
Hình choùp ñeàu
A
C
B
S
O
- Hình choùp tam giaùc ñeàu
- Hình choùp töù giaùc ñeàu
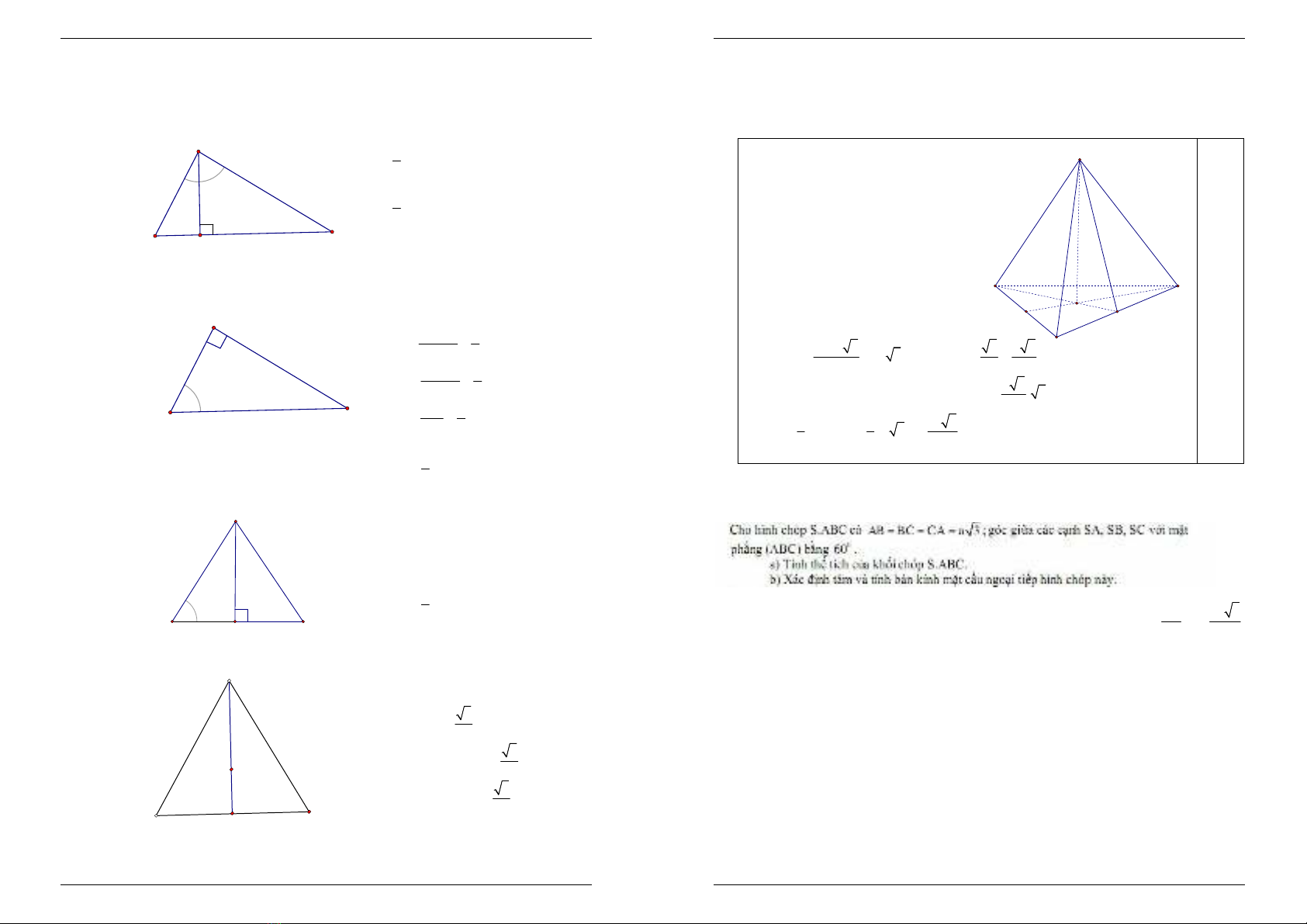
Thoâng thöôøng baøi toaùn veà hình laêng truï:
.
V B h
B: dieän tích ñaùy
h : ñöôøng cao
Laêng truï ñöùng ABC.A1B1C1 Laêng truï xieân ABC.A1B1C1
A1A
(ABC) A1G
(ABC)
A
C
B
B
1
C
1
A
1
H
A1
B
C
A
B
1
C1
G
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 3 Löu Tuaán Hieäp
HEÄ THOÁNG KIEÁN THÖÙC CÔ BAÛN
A. Các Tính Chất :
a. Tam giác :
Diện tích của tam giác
*
1
. . .sin
2
ABC
S AB AC A
* 1
. .
2
ABC
S BC AH
Các tam giác đặc biệt :
o Tam giác vuông :
+ Định lý pitago:
222
BC AB AC
+ Tỷ số lượng giác trong tam giác vuông
Ñoái
sin Huyeàn
b
B
a
Keà
cos Huyeàn
B
a
Ñoái
tan Keà
b
B
c
+ Diện tích tam giác vuông:
1
. .
2
ABC
S AB AC
o Tam giác cân:
+ Đường cao AH cũng là đường trung
tuyến
+ Tính đường cao và diện tích
.tan
AH BH B
1
. .
2
ABC
S BC AH
o Tam giác đều
+ Đường cao của tam giác đều
3
.
2
h AM AB
( đường cao h = cạnh x
3
2
)
+ Diện tích : 2
3
( ) .
4
ABC
S AB
h
H
A
BC
c
a
b
C
B
A
A
B
C
H
B
A
G
C
M
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 28 Löu Tuaán Hieäp
MỘT SỐ ĐỀ THI LIÊN QUAN ĐẾN THỂ TÍCH KHỐI ĐA DIỆN
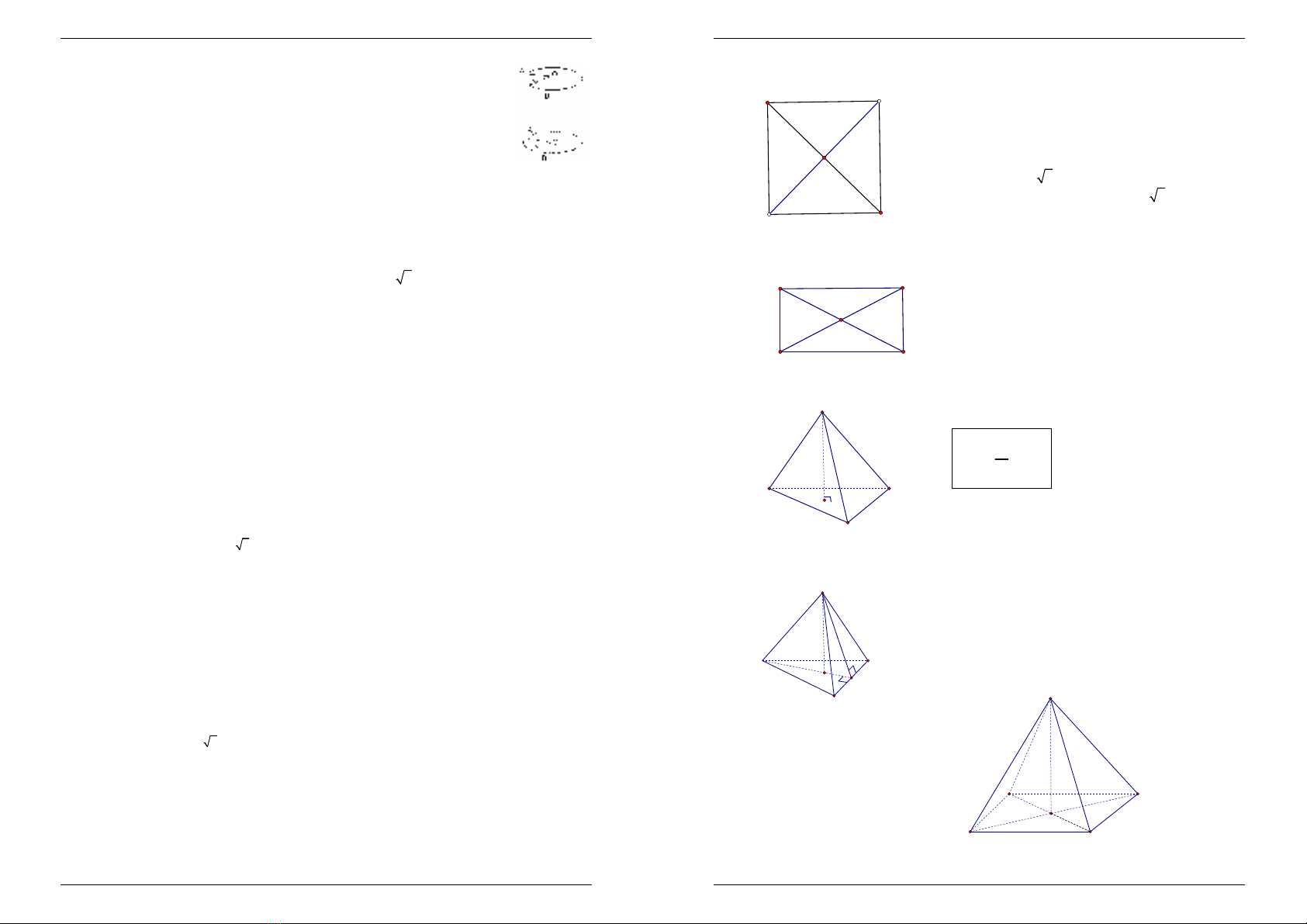
1. Đề Thi Học Kỳ 1- Năm học 2008-2009 (1,0 điểm)
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng 2a, góc giữa mặt bên và
mặt đáy bằng
0
60
. Tính thể tích của khối chóp S.ABC theo a.
2. Đề Thi Học Kỳ 1- Năm học 2009-2010 (2,0 điểm)
Đáp số : 3
3 2 3
,
4 3
a a
V R
Gọi O là tâm của đáy và M là trung điểm của BC
Do S.ABC là hình chóp tam giác đều nên:
0
( )
( );( ) 60
SO ABC
g SBC ABC SMO
Vì tam giác ABC là tam giác đều cạnh 2a nên:
22
(2 ) 3
4
ABC
a
S a
và
3 3
2
6 3
a
OM a
Xét tam giác vuông SMO: 03
.t an60 . 3
3
a
SO OM a
Vậy
3
2
1 1 3
. 3.
3 3 3
ABC
a
V S SO a a
0,25
0,25
0,25
0,25
2a
2a
2a
60
O
M
AC
B
S
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 27 Löu Tuaán Hieäp
Bài Tập Về Mặt Tròn Xoay
Bài 2.1 Một hình trụ có khoảng cách hai đáy bằng 7a .Cắt khối trụ bởi một
mặt phẳng song song với trục và cách trục một đoạn d = 3a theo một
thiết diện có diện tích S=56a2 .Tính diện tích xung quanh của hình trụ
và thể tích của khối trụ.
Bài 2.2 Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền
bằng a. Tính thể tích khối nón và diện tích xung quanh của hình nón đă cho.
Bài 2.3 Cho hình nón tròn xoay có đường cao h=a, bán kính đáy r=1,5a. Tính diện tích
xung quanh của hình nón và thể tích khối nón đã cho theo a.
Bài 2.4 Cho tam giác ABC vuông cân tại A,có BC=20
2
(cm). Hình nón tròn xoay khi
quay đường gấp khúc CBA xung quanh trục là đường thẳng chứa cạnh AB. Tính
Diện tích xung quanh của hình nón và Thể tích của khối nón.
Bài 2.5 Cho hình lập phương
' ' ' '
.
ABCD AB C D
có cạnh a .Gọi O là tâm hình vuông ABCD
a). Tính thể tích của hình chóp
' ' '
.
O A B C
b). Tính diện tích xung quanh và thể tích khối nón có đỉnh là O và đáy là hình tròn
nội tiếp hình vuông
' ' ' '
A B C D
Bài 2.6. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a có SA vuông
góc với đáy và SA = AC.
a). Tính thể tích khối chóp S.ABCD.
b). Khi quay tam giác SAB quanh trục SA tạo ra hình nón. Tính diện tích xung quanh
và thể tích của khối nón.
Bài 2.7. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a có SA vuông
góc với đáy cạnh
SB = a 3
.
a). Tính thể tích khối chóp S.ABCD.
b). Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD.
Bài 2.8. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I là
trung điểm của BC.
a). Tính thể tích khối chóp S.ABC và S.ABI theo a.
b). Một hình nón có đỉnh trùng với đỉnh của hình chóp và đáy là hình tròn ngoại tiếp
đa giác đáy của hình chóp. Tính diện tích xung quanh của hình nón và thể tích
khối nón.
Bài 2.9 Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với đáy.
Biết AB=a,
BC = a 3
, SA=3a.
a). Tính thể tích khối chóp S.ABC.
b). Xác định tâm và bán kính của mặt cầu ngoại tiếp khối chóp S.ABC.
Bài 2.10 Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với đáy.
Biết SA=AB=BC=a.
a). Tính thể tích khối chóp S.ABC.
b). Xác định tâm và bán kính của mặt cầu ngoại tiếp khối chóp S.ABC
Toaùn 12 Theå Tích Khoái Ña Dieän – Maët Troøn Xoay
Taøi lieäu löu haønh noäi boä 4 Löu Tuaán Hieäp
b. Tứ giác
Hình vuông
+ Diện tích hình vuông :
2
( )
ABCD
S AB
( Diện tích bằng cạnh bình phương)
+ Đường chéo hình vuông
. 2
AC BD AB
( đường chéo hình vuông bằng cạnh x
2
)
+ OA = OB = OC = OD
Hình chữ nhật
+ Diện tích hình vuông :
.
ABCD
S AB AD
( Diện tích bằng dài nhân rộng)
+ Đường chéo hình chữa nhật bằng nhau và
OA = OB = OC = OD
B. Thể Tích Khối Chóp: + Thể tích khối chóp
1
. .
3
V B h
Trong đó : B là diện tích đa giác đáy
h : là đường cao của hình chóp
Các khối chóp đặc biệt :
Khối tứ diện đều:
+ Tất cả các cạnh đều bằng nhau
+ Tất cả các mặt đều là các tam giác đều
+ O là trọng tâm của tam giác đáy
Và AO
(BCD)
B
Khối chóp tứ giác đều
+ Tất cả các cạnh bên bằng nhau
+ Đa giác đáy là hình vuông tâm O
+ SO
(ABCD)
O
B
D
A
C
O
AB
D
C
h
S
B
A
C
H
A
C
D
M
O
O
C
D
B
A
S