1
TỐI ƯU HÓA PHI TUYẾN
CHƯƠNG 3
Financial Modeling 1
3.1 GiỚI THIỆU MÔ HÌNH PHI TUYẾN
•Trên thực tếcó nhiều vấn đềtrong kinh tếvà trong các
hoạt động kinh doanh có những mối liên hệvới nhau
không phải là mối quan hệtuyến tính mà là phi tuyến.
•Sựtồn tại các mối quan hệkhông theo tỷlệ( doanh số
đạt được không theo tỷlệvới giá bán vì giá bán có thể
tăng và doanh sốcó thểgiảm.
•Sựtồn tại các mối quan hệkhông mang tính cộng bổsung
(rủi ro của danh mục sẽkhác với bình quân gia quyền của
2 chứng khoán trong danh mục này.
•Sựhiệu quảvà không hiệu quảtheo quy mô (khi sản
lượng tiêu thụvượt quá một mức giới hạn nào đó thì
tổng định phí và biến phí đơn vịsẽthay đổi)
Financial Modeling 2
2
3.1 GiỚI THIỆU MÔ HÌNH PHI TUYẾN
•Bất cứgiá trịnào của x mà tại đó đạo hàm riêng = 0 gọi là điểm dừng.
•Tại giá trịtối ưu địa phương (tối thiểu hoặc tối đa) tất cảcác đạo hàm riêng
phải = 0. Điểm tối ưu cực đại hoặc cực tiểu luôn là điểm dừng.
•Việc thiết lập các đạo hàm riêng cấp 1 bằng 0 trong một hàm n biến sẽtạo ra n
hệphương trình. Ngoại trừtrường hợp hệphương trình là tuyến tính, thì đối
với trường hợp hàm phi tuyến (ví dụhàm sốgốc là hàm bậc 3) không dễdàng
tìm lời giải và sẽkhông khảthi khi giải bằng tay.
•Điều kiện đủthứ2 khá phức tạp, yêu cầu phải tính toán các định thức của các
ma trận đạo hàm riêng cấp 2. Trên thực tế, ngay cảtrong trường hợp hàm f chỉ
có một hay hai biến sốnhưng quá phức tạp thì dường nhưchúng ta vẫn không
có khảnăng giải bằng thủcông bài toán tối ưu này.
Financial Modeling 3
3.2 TỐI ƯU HÓA PHI TUYẾN QUA ĐỒ
THỊ
Financial Modeling 4
3
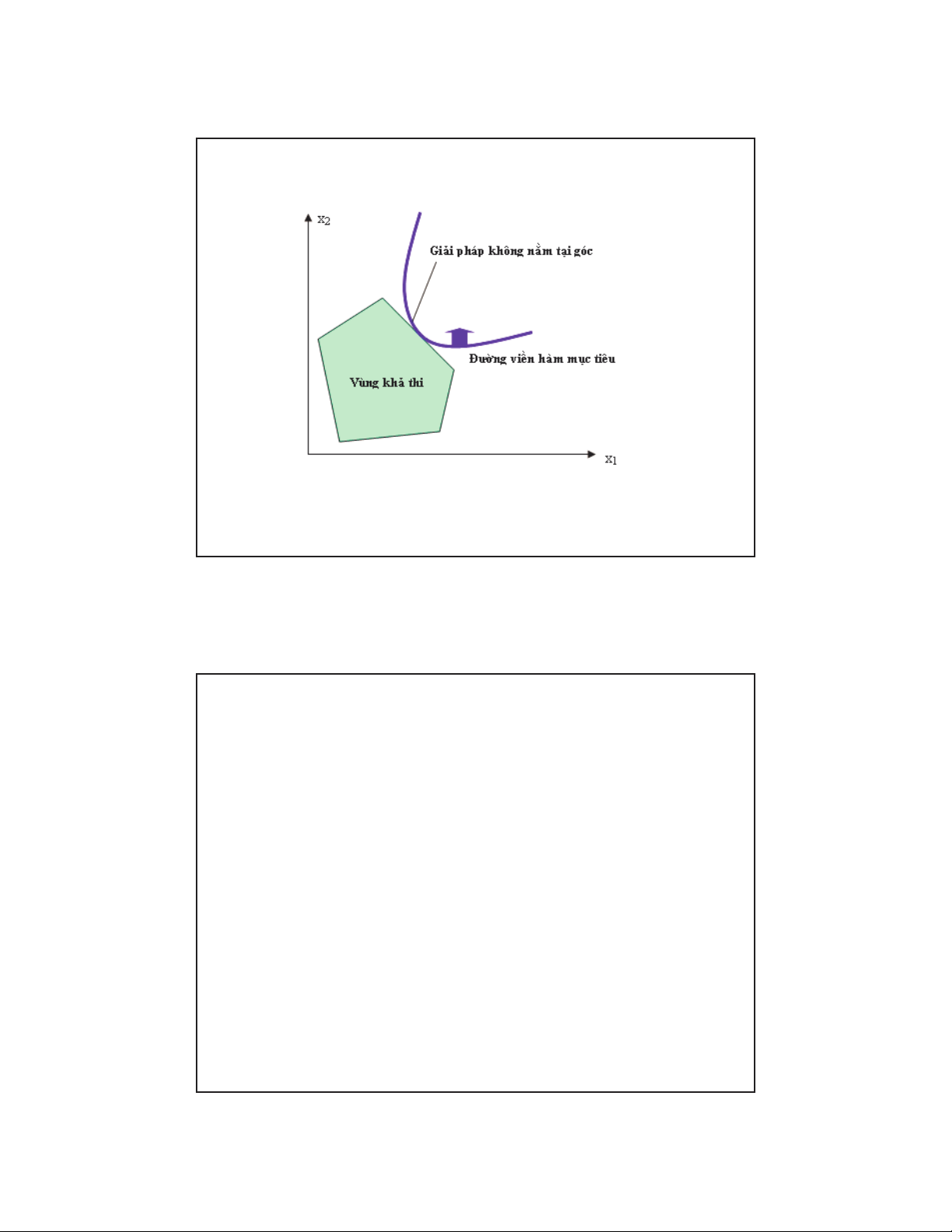
3.2 TỐI ƯU HÓA PHI TUYẾN QUA ĐỒ
THỊ
•Giải pháp tối ưu của mô hình phi tuyến không phải luôn luôn tại góc nhưcủa mô
hình tuyến tính
Financial Modeling 5
3.2 TỐI ƯU HÓA PHI TUYẾN QUA ĐỒ
THỊ
•Sựso sánh giữa LP và NLP
•Có một vài điểm tương đồng giữa LP và NLP. Ví dụ:
•Một sựgia tăng (hay giảm) RHS của bất phương trình
ràng buộc ≤ (≥) sẽnới lỏng điều kiện ràng buộc. Điều
này không làm co lại và có thểmởrộng vùng khảthi.
•Việc nới lỏng điều kiện ràng buộc không làm tổn hại
và có thểgiúp gia tăng giá trịmục tiêu tối ưu.
•Việc thắt chặt điều kiện ràng buộc không giúp ích và
có thểgây tổn hại giá trịmục tiêu tối ưu.
•
Financial Modeling 6
4
3.2 TỐI ƯU HÓA PHI TUYẾN QUA ĐỒ
THỊ
•Giá trịtối ưu địa phương (cực trịđịa phương) so với giá trịtối
ưu toàn cục (cực trịtoàn cục)
•Trong mô hình LP cực trịđịa phương cũng là cực trịtoàn cục
•Trong mô hình NLP có thểvừa có cực trịđịa phương và vừa có cựa
trịtoàn cục.
•Giá trịcực đại toàn cục là điểm cực đại theo ràng buộc toàn cục
bởi vì giá trịcủa hàm mục tiêu tại điểm này là lớn nhất so với tất
cảcác điểm khảthi khác.
•Trong mô hình NLP đểtìm ra cực trịtoàn cục từcác cực trịđịa
phương cần phải bổsung các điều kiện các điều kiện lồi và điều
kiện lõm. Những điều kiện này phải được thỏa mãn đểđảm bảo
rằng giá trịtối ưu hóa địa phương cũng sẽlà giá trịtối ưu hóa toàn
cục.
Financial Modeling 7
3.2 TỐI ƯU HÓA PHI TUYẾN QUA ĐỒ
THỊ
Financial Modeling 8
5
3.3 SỬDỤNG SOLVER CHO MÔ HÌNH PHI TUYẾN
Financial Modeling 9
• Trong mô hình LP, Solver sử dụng phương pháp di chuyển từ
góc này sang góc khác trong các vùng khả thi.
•
Trong mô hình NLP, Solver sử dụng phương pháp “leo dốc” dựa
trên tiến trình tìm kiếm ñộ dốc ñược giảm thiểu chung và
phương pháp này còn ñược gọi là GRG.
• Các bước của tiến trình này ñược thực hiện như sau:
• Sử dụng các giá trị ban ñầu của các biến số quyết ñịnh tính
toán một hướng ñi ñược sao cho cải thiện nhanh nhất giá trị
của hàm mục tiêu.
• Solver lại thử một hướng tính toán mới từ một ñiểm khởi sự
mới, tiến trình trên ñược lặp lại cho ñến khi giá trị OV không
còn ñược cải thiện tốt hơn trên bất kỳ một hướng mới nào thì
tiến trình tìm kiếm giá trị tối ưu kết thúc.
3.4 MÔ HÌNH QUẢN LÝ HÀNG TỒN
KHO EOQ
•Kiến thức nền tài chính
•Các chi phí liên quan đến tồn kho
Tại cùng một thời điểm khi một doanh nghiệp được
hưởng những lợi ích từviệc sửdụng hàng tồn kho thì
các chi phí có liên quan cũng phát sinh tương ứng, bao
gồm:
•Chi phí đặt hàng (Ordering costs)
•Chi phí tồn trữ(Carrying costs)
•Chi phí thiệt hại do kho không có hàng (Stockout costs)
Financial Modeling 10