
TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI
I- MỤC TIÊU
- HS nắm vững nội dung định lí về trường hợp đồng dạng thứ hai
- Hiểu được phương pháp chứng minh định lí
- Vận dụng định lí để nhận biết tam giác đồng dạng
- Vận dụng giải bài tập tính toán và làm bài tập chứng minh.
II- CHUẨN BỊ
GV:Thước kẻ, bảng phụ, com pa.
HS: Thước thẳng ,com pa
III- TIẾN TRÌNH DẠY HỌC
HOẠT ĐỘNG CỦA GV HOẠT ĐỘNG CỦA HS
HĐ1: Kiểm tra bài cũ:(5 phút)
GV: Phát biểu trường hợp đồng dạng thứ
nhất?
GV gọi HS nhận xét và cho điểm
Hoạt động 2: Bài mới (30 phút)
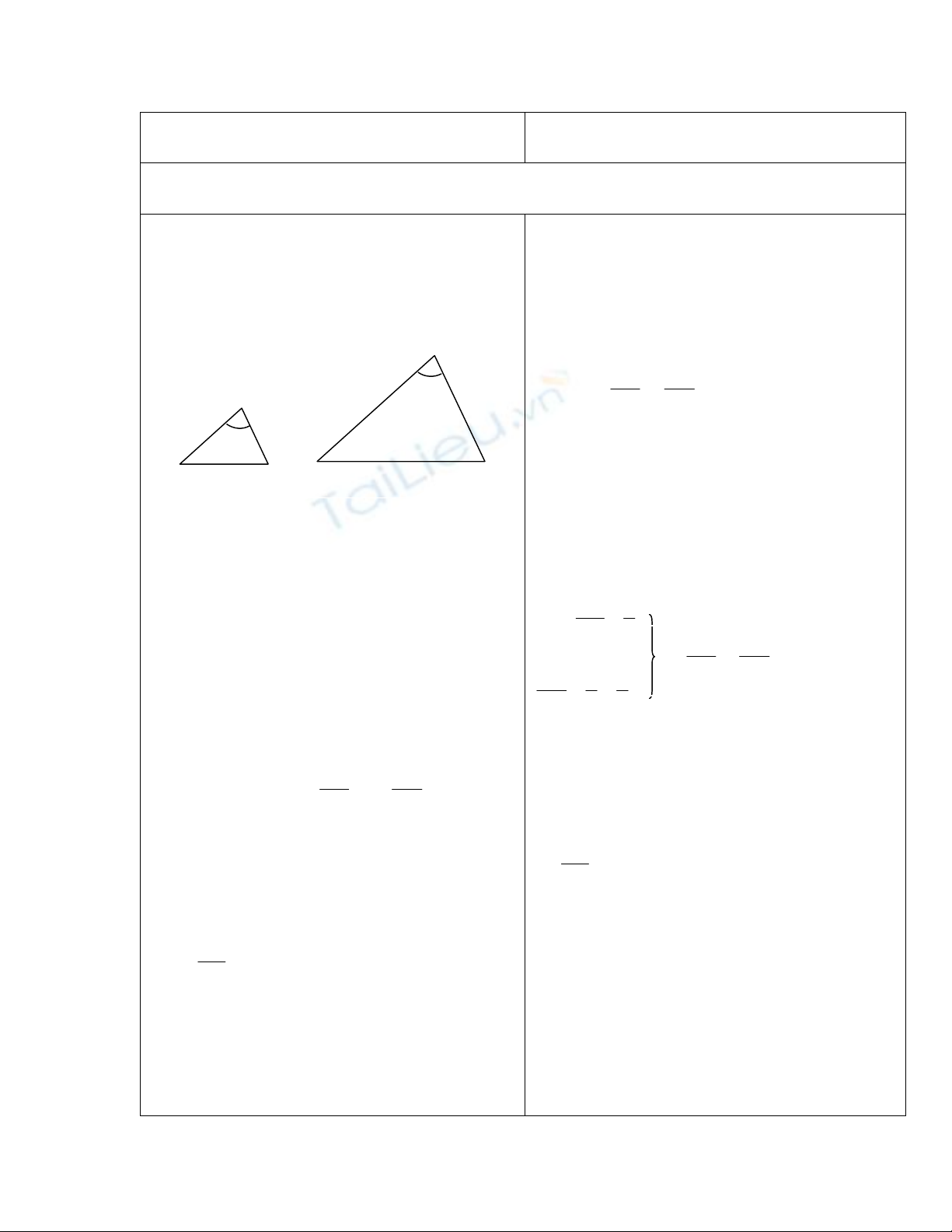
GV: Nghiên cứu ?1 ở trên bảng phụ
+ So sánh các tỉ số
AB
DE
Và
AC
DF
+ Đo các đoạn thẳng BC, EF
Tính
BC
EF
. Dự đoán sự đồng dạng ABC
và DEF?
+ Đó là nội dung định lí trường hợp đồng
1. Định lí
?1
So sánh
AB
DE
=
AC
DF
+ Dự đoán sự đồng dạng của
ABC và
DEF ?
HS:
4
3
AB
DE
8 4
6 3
AC
DF
HS : Đo các đoạn thẳng, sau đó thính tỉ
số
BC
EF
=> kết luận
* Định lí : SGK/75
HS : Phát biểu thành lời
D
600
A 8 6
4 600 3
B C E F
=>
AB
DE
=
AC
DF
dạng thứ hai. Hãy phát biểu bằng lời?
+ Suy nghĩ và tìm phương pháp chứng
minh định lí trên?
+ yêu cầu HS tự trình bày phần chứng
minh?
+ Chữa và chốt lại phương pháp chứng
minh.
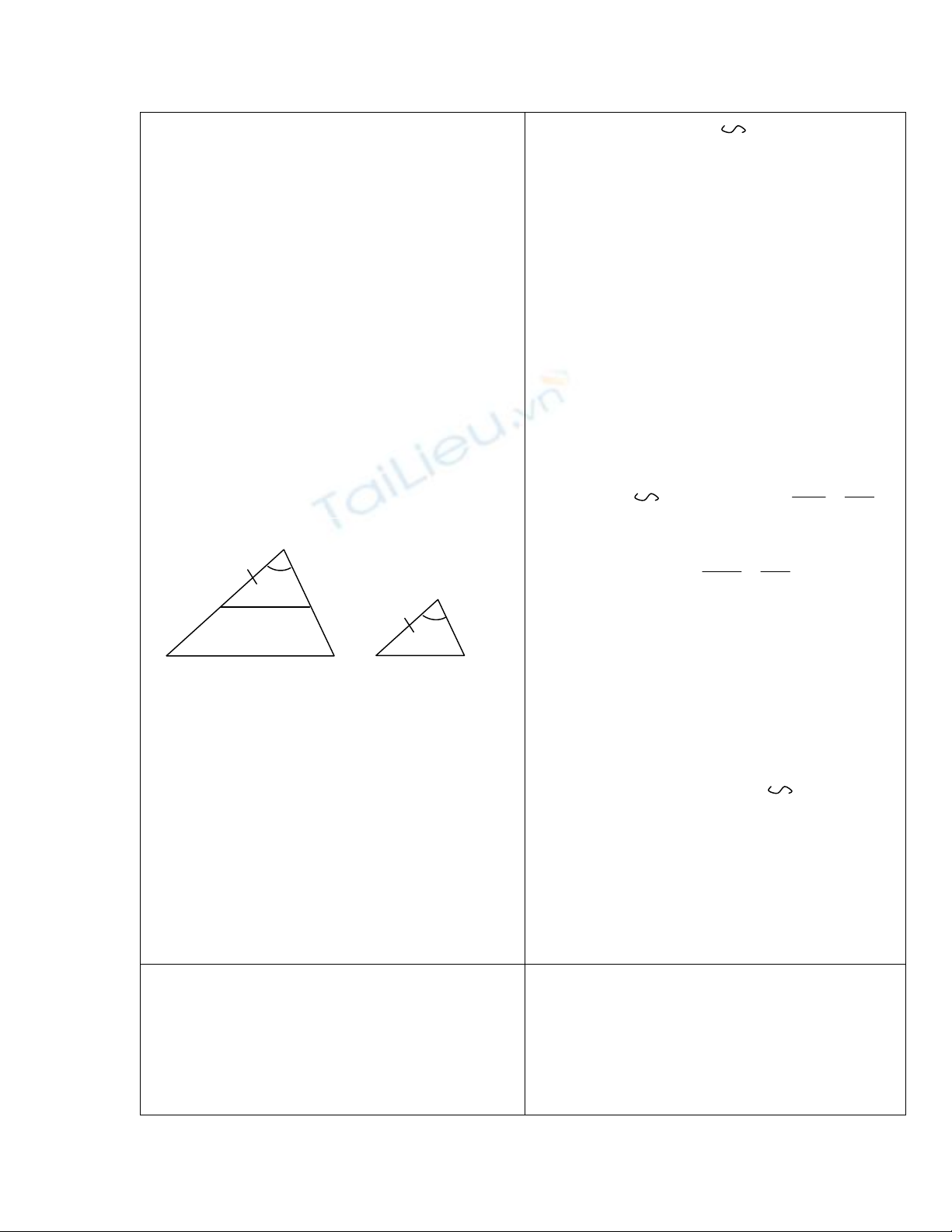
HS : B1: Tạo AMN
ABC
B2: CMR: AMN = A’B’C’
B3: kết luận
HS trình bày ở phần ghi bảng
Lấy M AB; AM = A’B’
kẻ MN//BC
=> AMN
ABC (1) =>
AM AN
AB AC
Vì AM = A’B’ => ' '
A B AN
AB AC
=> AN
=A’C’
Chứng minh được :
AMN = A’B’C’ (2)
Từ (1) và (2) => A’B’C’
ABC
GV: Nghiên cứu ?2 và hoạt động theo
2. áp dụng
?2
A
M N A'
B C B' C'
nhóm?
- Yêu cầu HS đưa ra kết quả nhóm, sau
đó chốt phương pháp
HS hoạt động theo nhóm
HS đưa ra kết quả nhóm
ABC DEF vì:
1
2
AB AC
DE DF
Và A = D = 700
DEF không đồng dạng PQR...
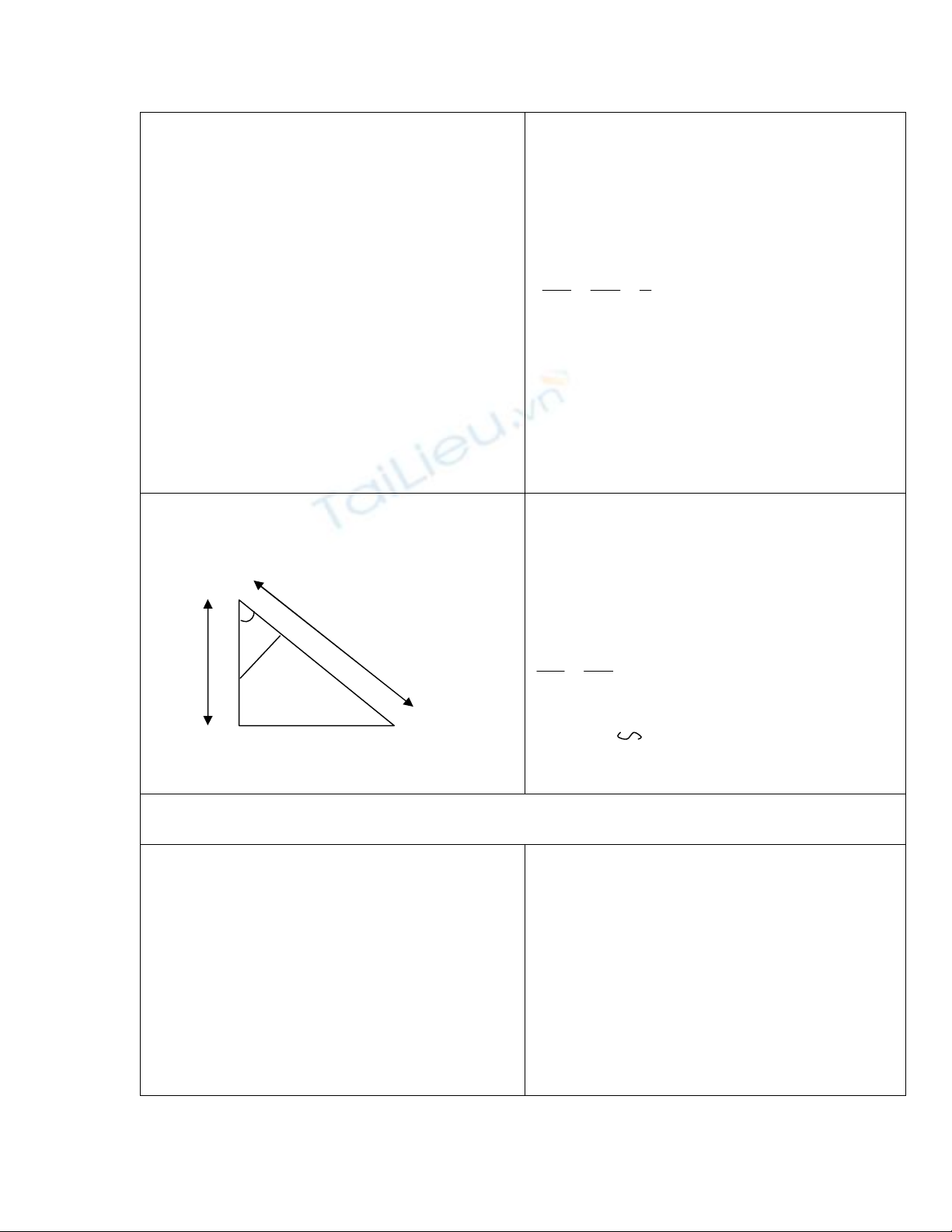
GV: Các nhóm làm ?3 ở bảng phụ
HS : trình bày ?3
Xét AED và ABC có:
AE AD
AB AC
=>AED
ABC (c.g.c)
Hoạt động 3: Củng cố (8 phút)
- Vẽ hình minh hoạ cho trường hợp đồng
dạng thứ hai
- bài tập 32/77 SGK
? Để chứng minh 2 tam giác đồng dạng
em có những cách nào ?
HS.........
HS ……..
A
2
500 E 7,5
3
5 D
B C

Hoạt động 4: Giao việc về nhà (2 phút)
- Học thuộc các định lí, xem lại phần
chứng minh
- BTVN: 34, 33/77
* Hướng dẫn bài 34: Gọi hai trung tuyến
tương ứng là A'M' và AM, từ A’B’C’
ABC => A’B’M’
ABM (c.g.c)
=> k
AB
BA
AM
MA ''''
















