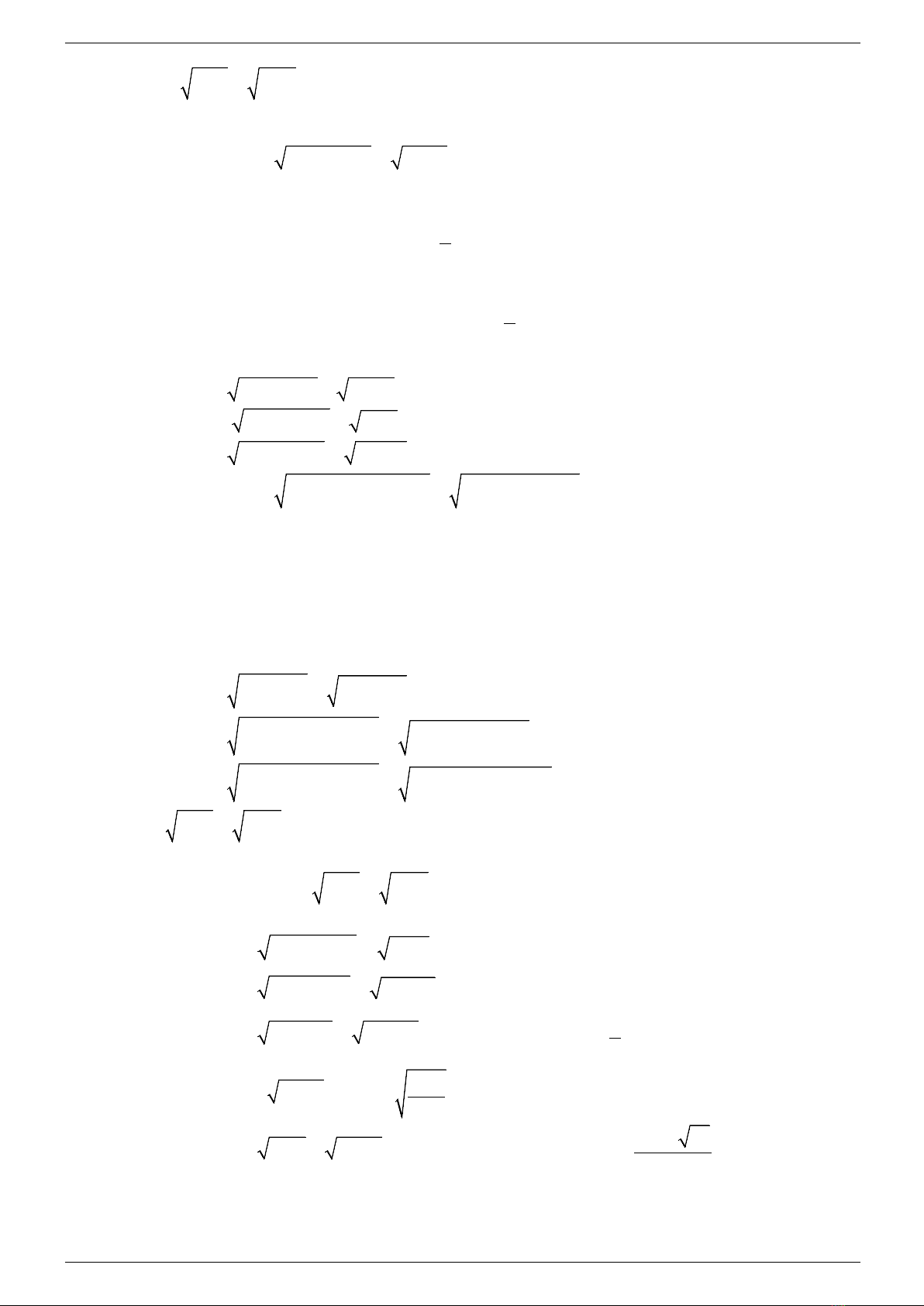Tailieumontoan.com

Điện thoại (Zalo) 039.373.2038
TUYỂN TẬP CÁC PHƯƠNG PHÁP
GIẢI TOÁN PHƯƠNG TRÌNH VÔ TỶ
Tài liệu sưu tầm, ngày 8 tháng 12 năm 2020
Website: tailieumontoan.com
Chương 1:
PHƯƠNG PHÁP GIẢI TOÁN VÀ CÁC KỸ THUẬT XỬ LÝ
Chương này giới thiệu cùng bạn đọc:
- Các phương pháp giải phương trình vô tỷ điển hình.
- Rèn luyện kỹ năng sử dụng phương pháp giải toán.
- Phân tích sai lầm và giải quyết các khó khăn của mỗi phương pháp.
- Phân tích ưu điểm và nhược điểm của mỗi phương pháp giải toán.
- Những góc nhìn mới cho những dạng bài toán cũ.
- Trải nghiệm một số phương pháp giải toán và kỹ thuật mới lạ như: Khép chặt miền nghiệm để đánh giá,
truy ngược dấu biểu thức liên hợp…
A. PHƯƠNG PHÁP NÂNG LÊN LŨY THỪA
1. Một số dạng toán cơ bản.
- Dạng toán 1.
( ) ( ) ( )
g(x) 0 hoaëc f(x) 0
fx gx f(x) g(x)
≥≥
= ⇔ =
Ví dụ 1. Giải phương trình
2
2x 1 x 2x 5−= + −
Lời giải
2
2x 1 x 2x 5−= + −
2
2x 1 0
x 2x 5 2x 1
−≥
⇔+ −= −
2
1
x2
x4
≥
⇔
=
1
x2
x2
x2
≥
⇔= −
=
x 2.⇔=
- Kết luận. Nghiệm của phương trình đã cho là
x 2.=
- Lưu ý. Các bạn để ý rằng việc chọn
f(x) 2x 1 0= −≥
sẽ khiến chúng ta giải quyết bài toán một cách đơn
giản hơn việc chọn
Bài tập tương tự.
1) Giải phương trình
2
4 x x 3x 4.−= + +
2) Giải phương trình
2
2x 3x 1 5 x.+ −= −
3) Giải phương trình
2
2x 3 x 2x 2.+= + +
Ví dụ 2. Giải phương trình
33
x 3x 1 x 2x 5.− += + −
Lời giải
33
x 3x 1 x 2x 5− += + −
3
33
x 2x 5 0
x 3x 1 x 2x 5
+ −≥
⇔− += + −
3
x 2x 5 0
5x 6
+ −≥
⇔=
3
x 2x 5 0 (Voâ nghieäm)
6
x5
+ −≥
⇔=
- Kết luận. Phương trình đã cho vô nghiệm.
- Lưu ý. Trong việc giải phương trình vô tỷ nếu việc tìm những giá trị của x để
g(x) 0≥
là phức tạp,
chúng ta nên triển khai việc tìm nghiệm của phương trình sau đó thử vào điều kiện để xét xem nghiệm
vừa tìm được có thỏa mãn điều kiện bài toán hay không.
Chẳng hạn bài toán trên ta cần thử xem
6
x5
=
có thỏa mãn điều kiện
3
f(x) x 2x 5 0= + −≥
không bằng
cách thay trực tiếp giá trị cần tìm được vào hàm f(x), ta sẽ thấy
6 109
f0
5 125

=−<


, nên giá trị
6
x5
=
không
là nghiệm của phương trình đã cho.
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 1
Website: tailieumontoan.com
Bài tập tương tự.
1) Giải phương trình
32 2
x 2x 1 x (x 2) 3x.+ += + +
2) Giải phương trình
44
x 1 x 3x 1.+= − +
3) Giải phương trình
3 32
x 1 x x 5.−= + −
Ví dụ 3. Giải phương trình
32 3
x x 4 x 3x 1.+ −= − +
Lời giải
32 3
x x 4 x 3x 1+ −= − +
32
32 3
x x 40
x x 4 x 3x 1
+ −≥
⇔+ −= − +
32
2
x x 40
x 3x 5 0
+ −≥
⇔+ −=
32
x x 40
(Vo â nghieäm)
3 29
x2
+ −≥
⇔−±
=
- Kết luận. Phương trình đã cho vô nghiệm.
- Lưu ý. Với những bài toán có nghiệm số phức tạp hơn, ta có thể làm như sau:
32 2
f(x) x x 4 (x 3x 5)(x 2) 11x 14= + −= + − − + −
2
= (x 3z 5)(x 2) g(x)+− −+
3 29 3 29
fg0
22

−± −±
⇒=<



Bài tập tương tự.
1) Giải phương trình
32 3
xx xx1.+ = ++
2) Giải phương trình
4 42
xx xx1.+= + −
3) Giải phương trình
53 2 3
x 2x (x 2)(x 1).−= − +
Ví dụ 4. Giải phương trình
33
x(x 3x 1) x(x x).−+= −
Lời giải
33
x(x 3x 1) x(x x)−+= −
3
33
x(x x) 0
x(x 3x 1) x(x x)
−≥
⇔− += −
3
x(x x) 0
x(2 x 1) 0
−≥
⇔−=
3
x(x x) 0
x0
1
x2
−≥
=
⇔
=
x 0.⇔=
- Lưu ý.
- Sai lầm thường gặp là biến đổi phương trình về dạng:
33
x( x 3x 1 x x) 0−+− −=
Nguyên nhân:
A.B A. B=
chỉ đúng trong trường hợp
A0
B0
≥
≥
- Hướng khắc phục:
A.B A.C=
A.C 0 (hoaëc AB 0)
A(B C)=0
≥≥
⇔−
Bài tập tương tự.
1) Giải phương trình
22
x(x 2x 3) x(x 1).++= +
2) Giải phương trình
22 2 2
(x 1) (x x 1) (x x)(x 3).+ −+ = + +
3) Giải phương trình
22 3 2
(x 1) (x x 1) (x 1)(x x 2).− ++ = − + −
- Tổng quát:
nn
f(x) g(x)=
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 2
Website: tailieumontoan.com
-Dạng toán 2.
( ) ( ) ( ) ( )
33
fx gx fx gx= ⇔=
g(x) 0 (hoaëc f(x) 0)
f(x) = g(x)
≥≥
⇔
(Vôùi n , n 2 vaø n chaün)∈≥
Ví dụ 1. Giải phương trình
33
32 3
x 2x 1 x x.− += −
Lời giải
Phương trình đã cho tương đương với:
32 3
x 2x 1 x x− += −
2
2x x 1 0⇔ −−=
1
x2
x1
= −
⇔=
- Kết luận. Tập nghiệm của phương trình đã cho là
1
T ;1 .
2

= −


Bài tập tương tự.
1) Giải phương trình
33
22
x 2x 1 x x.+ += +
2) Giải phương trình
332 3
x 2x 1 x 3.+ += +
3) Giải phương trình
3
342 3
x 3x 1 1 2x .− += −
Ví dụ 2. Giải phương trình
( )
( )
( )
( )
32
33
x 1 x 2x 2 x 1 x 2x .− −+= − −
Lời giải
Phương trình đã cho tương đương với:
( )
( )
( )
( )
32
x 1 x 2x 2 x 1 x 2x− −+=− −
( )
( )
32
x1x x 2 0⇔− −+=
x1
x1
=
⇔= −
- Kết luận. Tập nghiệm của phương trình đã cho là
{ }
T 1;1 .= −
Bài tập tương tự.
1) Giải phương trình
( )
( )
33
3
3
x x 1 x x 1.+= +
2) Giải phương trình
( )
( ) ( )( )
22 22
33
x1 x x1 x xx 3.+ −+ = + +
3) Giải phương trình
( )
( )
( )
( )
22 32
33
x1 x x1 x1x x 2− ++ = − + −
.
- Tổng quát:
( ) ( ) ( ) ( ) ( )
nn
f x g x f x g x Vôùi n , n 2 vaø n leû= ⇔ = ∈≥
- Lưu ý. Chúng ta cần phân biệt rõ đâu là cách làm của thuộc dạng toán 1, đâu là cách làm thuộc dáng
toán 2 khi đứng trước dạng toán
( ) ( )
nn
fx gx.=
-BÀI TẬP RÈN LUYỆN.
Bài 1. Giải phương trình
2
x 2x 4 2 x.+ += −
Đáp số.
{ }
T = 2; 1 .−−
Bài 2. Giải phương trình
323
x 4x 2 3x 10.− += −
Đáp số.
{ }
T = 3; 4 .
Bài 3. Giải phương trình
32
2x 3x x 2x.−= −
Đáp số.
1
T = ;0 .
2

−


Bài 4. Giải phương trình
( )
2
x3
2x 9 x 5 .
x3
+
−= + −
Đáp số.
{ }
T = 3;1 .−
Bài 5. Giải phương trình
3
x3 5x3.+= +
Đáp số.
15 3 33
x = 1; x = .
2
+
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 3
Website: tailieumontoan.com
-Dạng toán 3.
( ) ( ) ( )
( ) ( )
2
gx 0
fx gx fx gx
≥
= ⇔ 
=

Ví dụ 1. Giải phương trình
2
x 2x 4 x 1.− +=−
Lời giải
2
x x4 x1+−=−
( )
2
2
x10
x x4 x1
−≥
⇔−−= −
x1 x5
x5
≥
⇔ ⇔=
=
- Kết luận. Nghiệm của phương trình đã cho là
x 5.=
Bài tập tương tự.
1) Giải phương trình
2
4x 2x 1 2x 1.+ += −
2) Giải phương trình
2
2x 3x 1 1 x.+ +=−
3) Giải phương trình
2
2x x 1 3x 1.++= −
Ví dụ 2. Giải phương trình
42 2
x 2x 2 1 x .+ −=−
Lời giải
42 2
x 2x 2 1 x+ −=−
( )
2
2
42 2
1x 0
x 2x 2 1 x
−≥
⇔+ −= −
2
1x1
4x 3
−≤ ≤
⇔=
1x1 3
x
32
x2
−≤ ≤
⇔ ⇔=±
= ±
- Kết luận. Tập nghiệm của phương trình đã cho là
33
T ;.
22


= −



Bài tập tương tự.
1) Giải phương trình
42 2
x x 4 x 2.+ += +
2) Giải phương trình
3
x x 1 1 x.++=−
3) Giải phương trình
63 3
x x 3 x 1.+ += +
Ví dụ 3. Giải phương trình
( ) ( )
2
x3 x1 x3.− −=−
Lời giải
( ) ( )
2
x3 x1 x3− −=−
( ) ( )
2
x30
x3 x1 1 0
−≥
⇔
− −−=

x3
x3 x 3.
x2
≥
⇔=
⇔=
=
- Kết luận. Nghiệm của phương trình đã cho là
x 3.=
- Lưu ý.
-Sai lầm thường gặp:
( ) ( )
2
x3 x1 x3− −=−
( )
x3 x1x3⇔ − −=−
( )
( )
x3 x11 0⇔ − −− =
x3
x2
=
⇔=
- Nguyên nhân sai lầm:
2
A,A 0
AA A,A 0
≥
= = −≤
- Hướng khắc phục:
( )
2
2
A0
A .B A A B1 0
≥
= ⇔ −=
Bài tập tương tự.
1) Giải phương trình
( ) ( )
2
x1 2x3 x1.+ +=+
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038 Trang 4