Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........70
Chú ý: M&i cung có mũi tên là mt hot ñng, nhưng có th bao gm nhiu hot
ñng nh khác. Nói cách khác, bn thân t"ng hot ñng ca d án có th li là mt
mng PERT nh.
Xác ñnh hot ñng găng, ñư#ng găng
Hot ñng găng là hot ñng mà
LST - EST = LFT - EFT = 0, hay [EST, EFT] ≡ [LST, LFT]
⇔
EST LST
EFT LFT
=
=
⇔
Slack LST EST 0
Slack LFT EFT 0
= − =
= − =
(ñ tr. cho phép bng 0).
Gii thích: Slack ≡ ñ ni lng (ñ tr.).
Trong ví d ñang xét, các hot ñng găng là: C → J → K → L (xem bng II.14) và
to thành ñưng găng (Critical Path). Vì vy, phương pháp mng PERT còn có tên là
phương pháp ñưng găng (CPM
−
Critical Path Method).
Xác ñnh ñư#ng găng bng phn mm Lingo
ð xác ñnh ñưng găng bng ph n mm Lingo, ta có th s# dng các bài toán mu
bng cách nhn vào biu tưng Lingo và thc hin các lnh File > Open > Pert.lng ñ
vào bài toán PERT mu. Sau ñó nhp các s liu ñ u vào ca bài toán c n gii vào thay
các s liu ca bài toán mu, ch-ng hn như s liu ca ví d ñã cho (xem hình III.6).
Hình III.6. Nhp s liu cho bài toán PERT
Sau ñó chúng ta thc hin LINGO > Solve, kt qu tính toán s, hin trên màn hình
(xem hình III.7).
Hình III.7. Kt qu tìm cung găng ca bài toán PERT
2.2. Sơ ñ7 PERT vi s! liu ng&u nhiên
Thi gian thc hin t"ng hot ñng ca d án nói chung là mt lưng bin ñng
khó d ñoán trưc, chúng ta gi thit chúng là các bin ngu nhiên. Gi s# ta có các s
liu ưc tính v thi gian thc hin các hot ñng ca d án (xem bng III.14) a, m, b.
Lúc ñó thi gian trung bình và ñ lch chu%n thi gian thc hin các hot ñng ñưc
ưc tính theo công thc
a 4m b
t
6
+ +
=
.
Bng III.14. S liu ưc tính v th#i gian thc hin các hot ñng
Thi gian ưc tính
Hot
ñng
Hot ñng
k trưc a
(sm
nht)
m
(nhiu kh năng xy
ra nht)
b
(mun
nht)
t
(thi gian
trung bình)
σ
(ñ lch tiêu chun,
ñ bin thiên)
A
B
C
D
E
F
G
H
I
J
K
L
−
−
−
A
A
E
B
B
D, F
C
H, J
G, I, K
1
1
1
1
2
0
3
2
1
4
1
4
2
2
2
2
3
0
6
5
4
9
2
4
3
3
3
9
10
0
15
14
7
20
9
4
2
2
2
3
4
0
7
6
4
10
3
4
1/3
1/3
1/3
4/3
4/3
0
2
2
1
8/3
4/3
0
Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........72
Bưc tip theo là lp sơ ñ mng cho d án vi các thi gian trung bình t và tìm
ñưng găng. ðưng găng là C → J → K → L bao gm các hot ñng găng C, J, K và L.
Các hot ñng này có ñ tr. cho phép bng 0, hay nói cách khác, không cho phép s
chm tr. nào. ðây là các hot ñng c n ht sc chú trng, vic chm thc hin bt c
mt hot ñng nào trong s này ñu kéo theo s chm tr. trong tin ñ ca c d án. T"
Critical Path (ting Anh) ñưc dch sang ting Vit là ñưng găng vì lí do ñó.
Thi gian thc hin d án là mt lưng ngu nhiên tính theo công thc: T = T
C
+ T
J
+ T
K
+ T
L
. Ta tìm kì vng ca T (thi gian trung bình thc hin d án) theo công thc:
m = m
T
= t
C
+ t
J
+ t
K
+ t
L
= 2 + 10 + 3 + 4 = 19 (tu n).
Tính ñ lch chu%n ca thi gian thc hin d án:
2 2 2
2
T C J K L
σ = σ = σ + σ + σ + σ
= 2 2 2
(1/ 3) (8 / 3) (4 / 3) 0
+ + +
= 3.
Ta coi T (thi gian thc hin d án) là bin ngu nhiên tuân theo lut chu%n
N(m = 19; σ = 3).
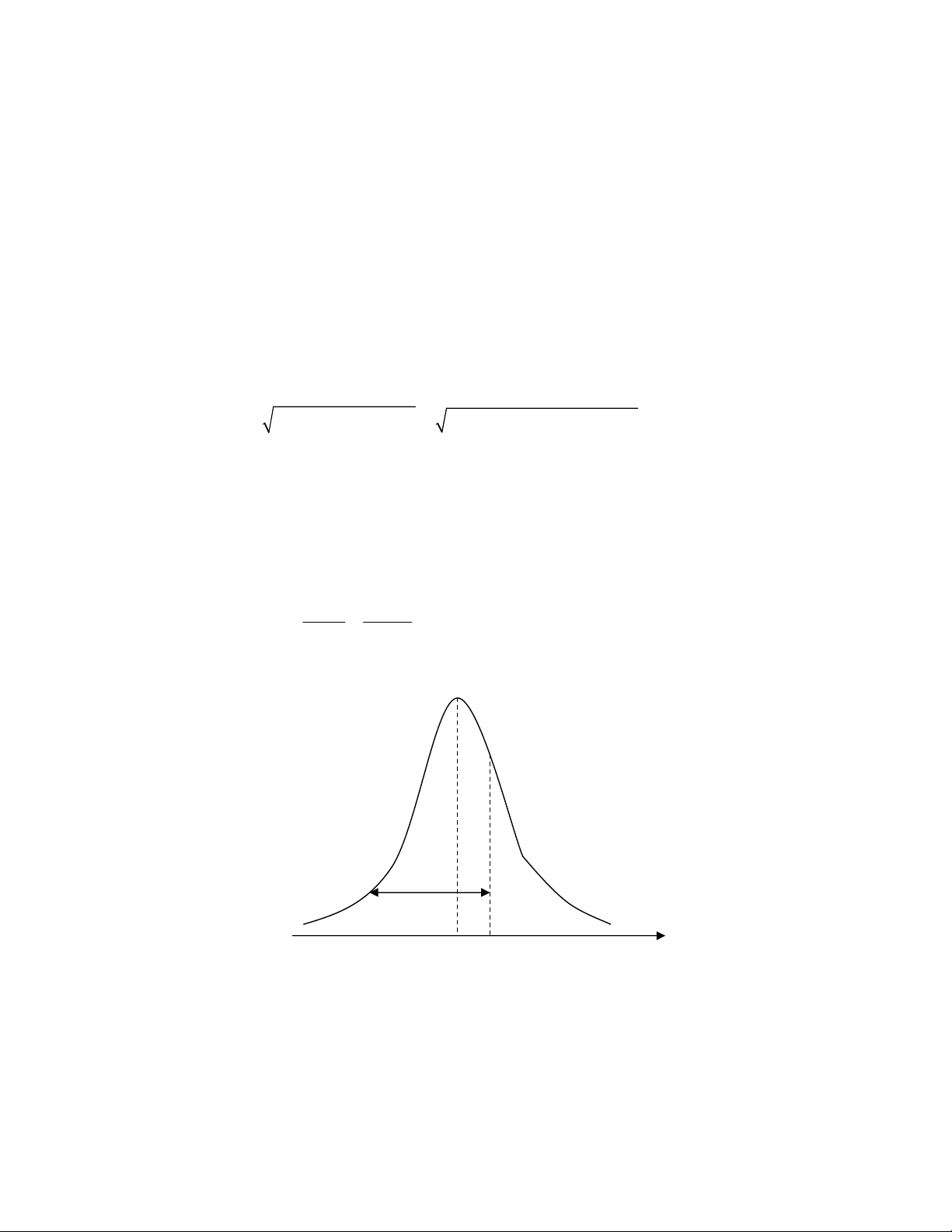
ð th hàm mt ñ xác sut ca T cho trên hình III.8.
ð tính P, xác sut thc hin d án trong vòng (không vưt quá) 19 tu n, ta phi
quy T v bin ngu nhiên vi phân phi chu%n tc N(0, 1) như cho trong ph lc 1. Lúc
ñó:
P(T ≤ 19) = P
T m 19 19
3
− −
≤
σ
= P(Z ≤ 0) = 0,5 (hay 50%),
*
ñ
ây Z = (T - m)/σ là bi
n ng
u nhiên tuân theo phân ph
i N(0, 1).
T
ươ
ng t
, xác su
t th
c hi
n d
án trong vòng (không v
ư
t quá) 21 tu
n
ñư
c tính
nh
ư
sau:
21 19 t
Hình III.8. ðưng cong mt ñ chu+n
75%
P(T ≤ 21) = P
T m 21 19
3
− −
≤
σ
= P (Z ≤ 0,666) = 75%.
Ta chuy
n sang xem xét v
n
ñ
v
ñ
tin c
y c
a th
i gian hoàn thành d
án. Ch
-
ng
h
n chúng ta mu
n tr
l
i câu h
i sau: Mu
n th
i gian th
c hi
n d
án có
ñ
tin c
y
90% thì th
i gian t
i thi
u (tính theo s
tu
n) là bao nhiêu?
ð$
t P (T ≤ t) = 90%. Tra
b
ng phân ph
i chu
%
n t
c N(0, 1), tìm
ñư
c z = 1,28. Vì z = (t − 19)/3 = 1,28 nên
t = 19 + 3. 1,28 ≈ 23 (tu
n). Nh
ư
v
y, d
án
ñ
ang xem xét có kh
n
ă
ng hoàn thành v
i
ñ
tin c
y t
i 90% trong vòng (không v
ư
t quá) 23 tu
n.
2.3. ðiu ch8nh d+ án khi k hoch mt s! hot ñng b phá v9
Ví d 4: ðôi khi trong quá trình thc hin d án, k hoch ca mt s hot ñng b
phá v. Chính vì vy, khi phát hin d án ñang b chm so vi k hoch ñ ra ta c n
ñnh li thi gian thc hin (thi gian rút gn) mt s hot ñng trong giai ñon ti. Xét
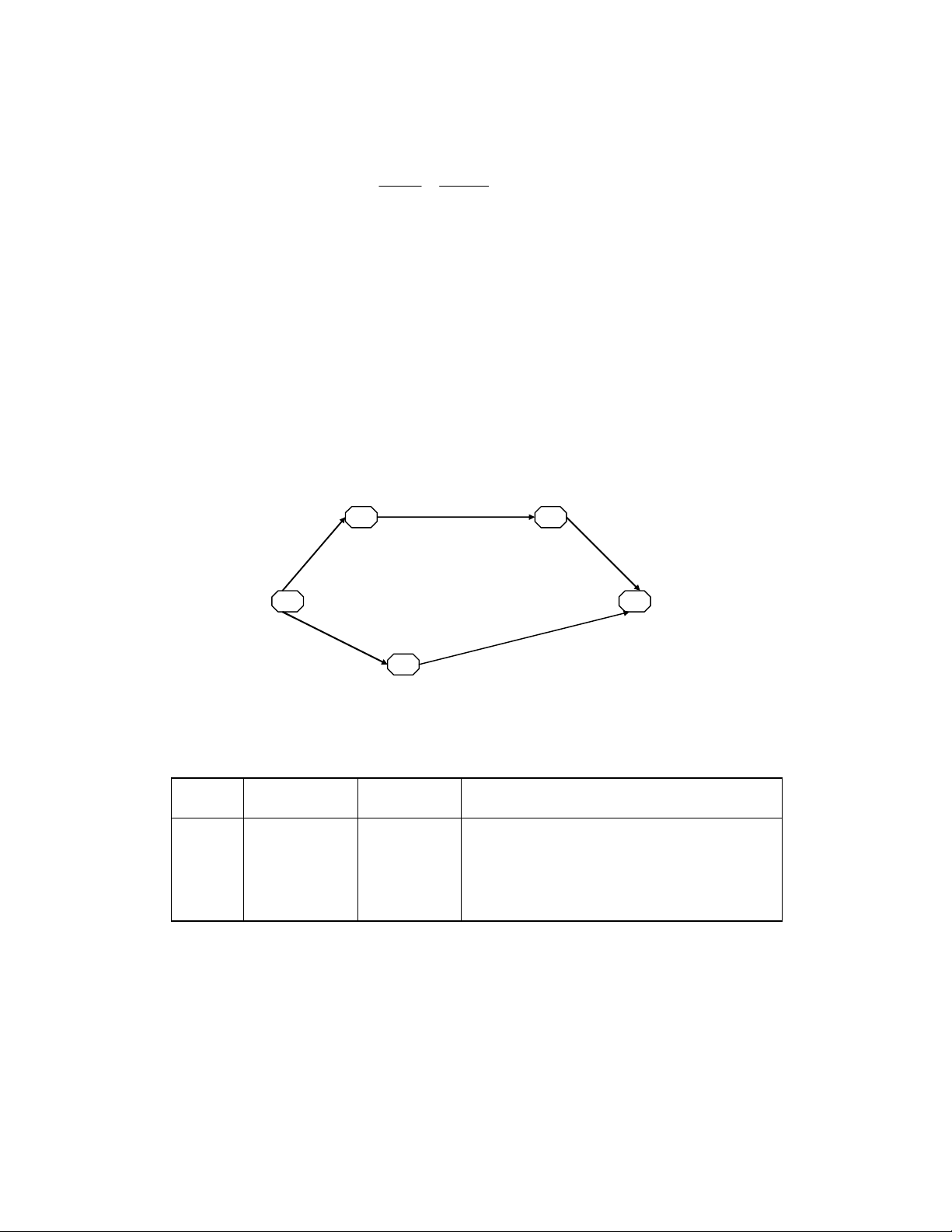
các d( kin cho trong hình III.9 và bng III.15.
Bng III.15. S liu ñiu ch%nh khi k hoach b phá v&
Hot
ñng
Thi gian ñnh
mc
Thi gian rút
gn
Kinh phí b sung/1ñơn v thi gian rút gn (triu
ñng)
A
B
C
D
E
6
4
3
8
7
4
3
2
6
4
2
3
1
1,5
0,5
Sau khi có thi gian ñnh mc cho các hot ñng như trong bng II.18, d. dàng tìm
ñưc thi gian ti thiu c n thit ñ hoàn thành k hoch là 16 (tu n). Tuy nhiên do yêu
c u mi, c n rút gn thi gian hoàn thành d án trong vòng (không vưt quá) 10 (tu n).
Mun vy ta thc hin các ñim sau:
− Tìm thi gian ti thiu d ñnh thc hin d án (16 tu n) và tìm ñưng găng.
− Ưc tính thi gian rút gn ti ña (ct 3, bng III.15).
2
1
3
4
5
A
C
D
B
E
Hình III.9. Sơ ñ mng PERT d án c n ñiu ch*nh
Trưng ði hc Nông nghip Hà Ni – Giáo trình Vn trù hc
………………………………..........74
− Khi rút gn thi gian trên ñưng găng cũng phi chú trng ñng thi các cung
ñưng khác.
Trên hình III.9, ta thy c n thc hin A, C và E vi thi gian rút gn ti ña (4, 2, 4
ñ tng các thi gian thc hin các hot ñng găng là 10 tu n), ñng thi rút gn các
hot ñng B và D * mc cho phép:
− Phương án 1: rút bt thi gian thc hin hot ñng B mt tu n và rút bt D mt
tu n.
− Phương án 2: không rút bt B và rút bt D hai tu n.
Vy khi c n ñiu chnh thi gian thc hin d án ta c n thay ñi k hoch ca mt
s hot ñng theo các bưc ñã nêu trên.
Tuy có nhiu phương án ñiu chnh d án, nhưng trong vic phá v k hoch các
hot ñng ca d án ñ ñáp ng tin ñ mi c n chú ý v khía cnh chi phí gia tăng ñ
có mt phương án ti ưu ñm bo rút gn ñưc thi gian thc hin vi chi phí nh nht.
ði vi ví d trên ta chn phương án 2.
Có th áp dng phương pháp tng quát ñ ñiu chnh d án theo các mc tiêu *
trên (phương pháp ñơn hình cho BTQHTT ñơn và ña mc tiêu) như s, ñưc trình
bày sau ñây.
2.4. Tính th(i gian rút gn t!i ưu b:ng phương pháp ñơn hình
ð tính thi gian rút gn bng phương pháp ñơn hình (có th s# dng các ph n
mm máy tính thích hp), ta phi ñưa ra ñưc mô hình toán hc, hay cách khác, c n
phát biu ñưc BTQHTT (ñơn hay ña mc tiêu).
Trưc ht, c n xác ñnh các bin quyt ñnh. Gi x
1
, x
2
, x
3
, x
4
, x
5
là các thi ñim
mà các hot ñng xy ra (ti các nút); y
A
, y
B
, y
C
, y
D
, y
E
là thi gian c n rút bt cho các
hot ñng ñ yêu c u mi v ñ%y nhanh tin ñ ñưc tho mãn. Ta có BTQHTT ña mc
tiêu sau (c n cc tiu hóa c thi gian thc hin d án ln tng chi phí gia tăng):
Mc tiêu 1: z
1
= x
5
→ Min
Mc tiêu 2: z
2
= 2y
A
+ 3y
B
+ y
C
+ 1,5y
D
+ 0,5y
E
→ Min
vi các ràng buc: