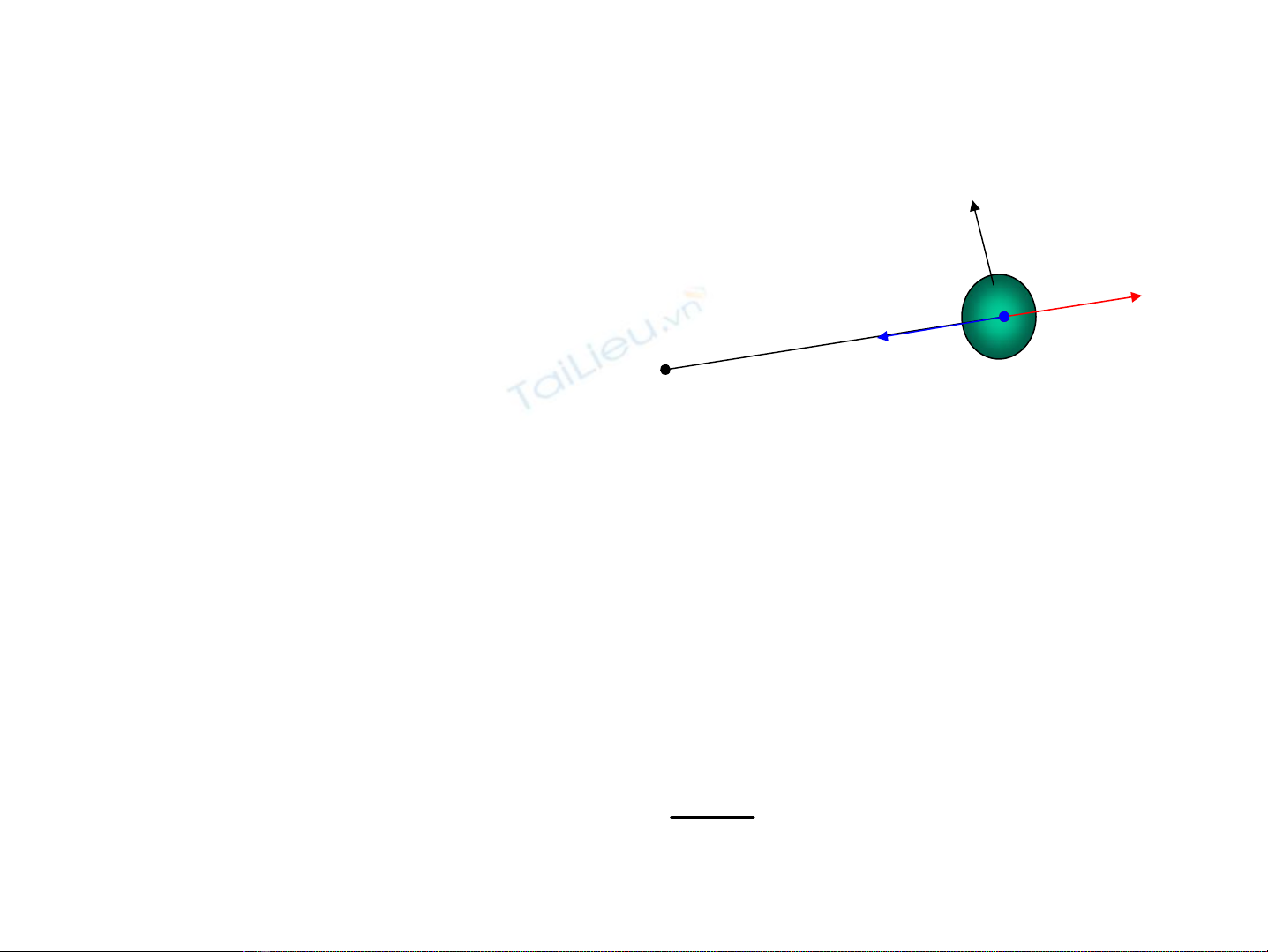
9Lùc h−íng t©m, lùc li t©m xuÊt hiÖn khi
chÊt ®iÓm chuyÓn ®éng cong: v
r
nLT FF r
r
−=
nHT FF
r
r
=
• Lùc h−íng t©m: kÐo chÊt
®iÓm vÒ phÝa lâm cña quÜ
®¹o:
FHT=T lùc c¨ng cña sîi d©y
• Lùc li t©m: lμmchÊt®iÓmv¨ngvÒphÝa
låicñaquÜ®¹o c©nb»ngvíilùch−íng
t©m
R
v
mFF 2
LTHT ==
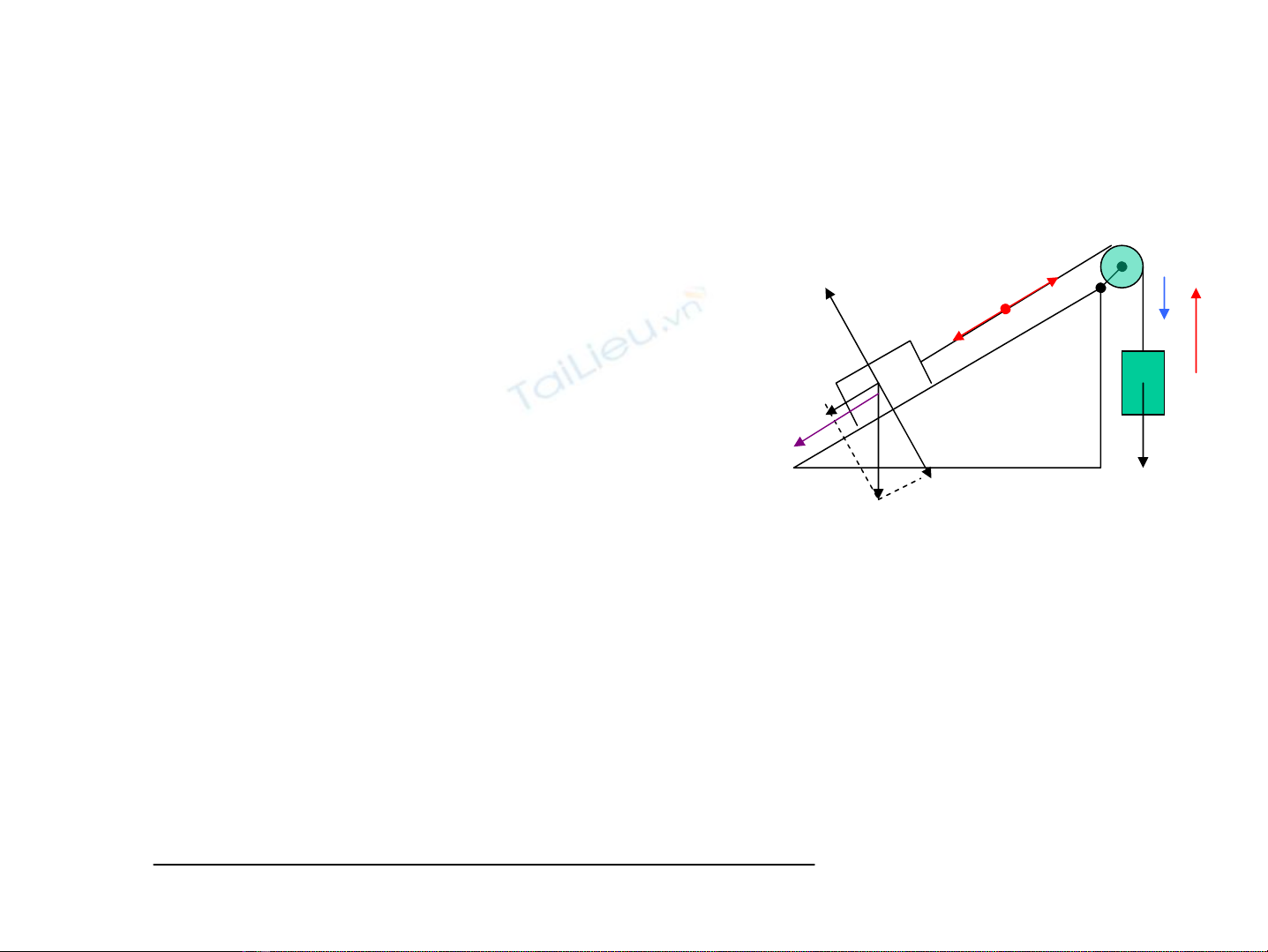
5. 3.VÝ dô: HÖ gåm mA, mB, hÖ sè ma s¸t k,
d©y kh«ng gi·n, rßng räc kh«ng ma s¸t vμkhèi
l−îng
B
P
r
1
T
r
2
T
r
A
P
r
2
P
r
1
P
r
N
r
α
Lùc ph¸t ®éng: PB
Lùc c¶n P1+fms
Lùc tæng hîp:PB-P
1-fms
)cosk(singmgma)mm( ABBA
α
+
α
−
=
+
)mm(
)cosk(singmgm
a
BA
AB
+
α
+
α
−
=
a>0 ®óng
a<0 gi¶ thiÕt chiÒu chuyÓn ®éng l¹i
ms
f
r
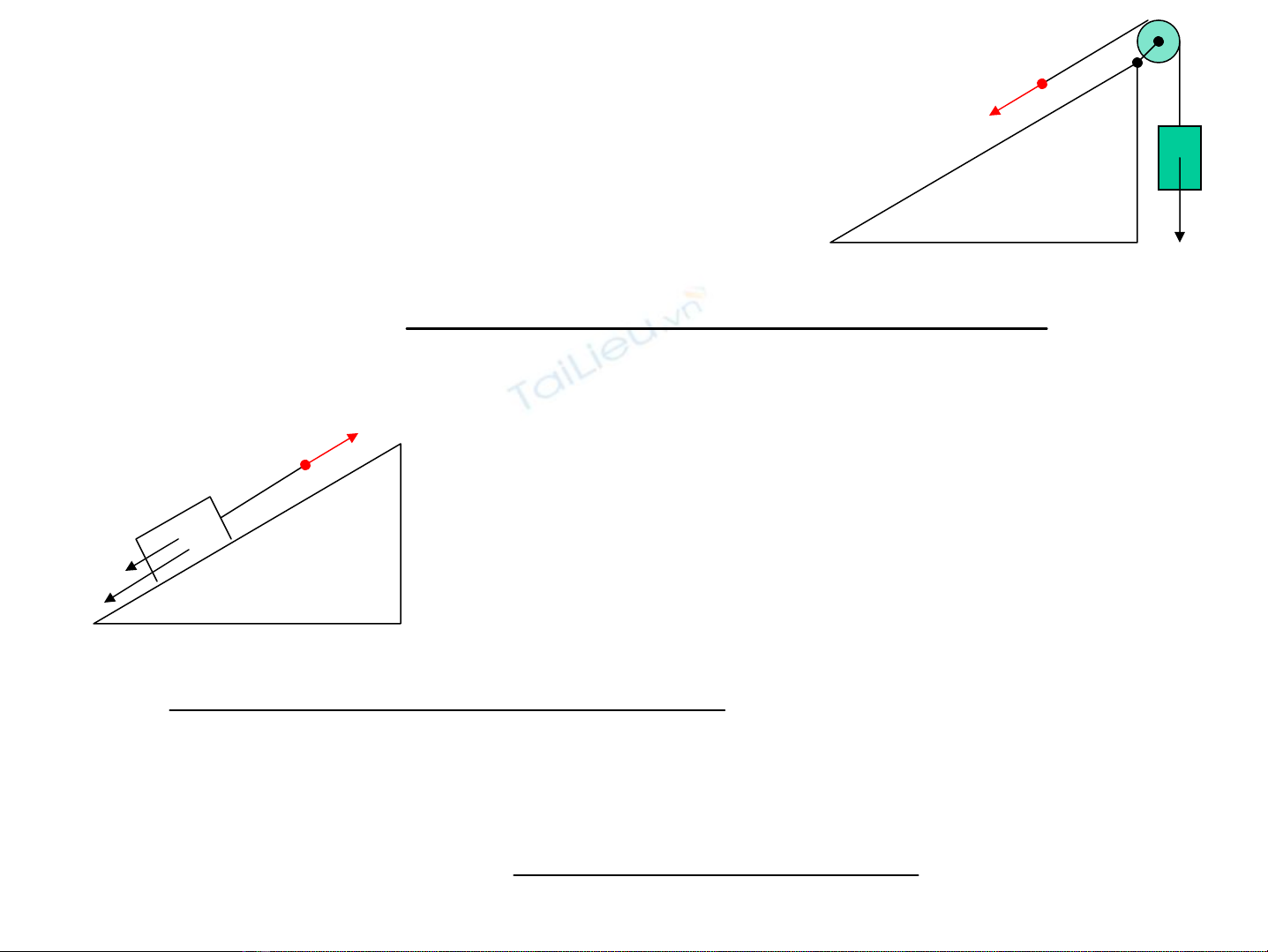
B
P
r
2
T
r
α
2BB TPa.m
=
amPTTT BB21
−
=
=
=
)mm(
)cosk(singmgm
mgmT
BA
AB
BB +
α
+
α
−
−=
ms11A fPTam
−
−
=
ms1A12 fPamTTT
+
+
=
=
=
α+α+
+
α
+
α
−
=cosgkmsin.gm
)mm(
)cosk(singmgm
mT AA
BA
AB
A
)mm(
)cosk(sin1
.gmmT
BA
BA +
α
+
α
+
=
1
T
r
1
P
r
α
ms
f
r
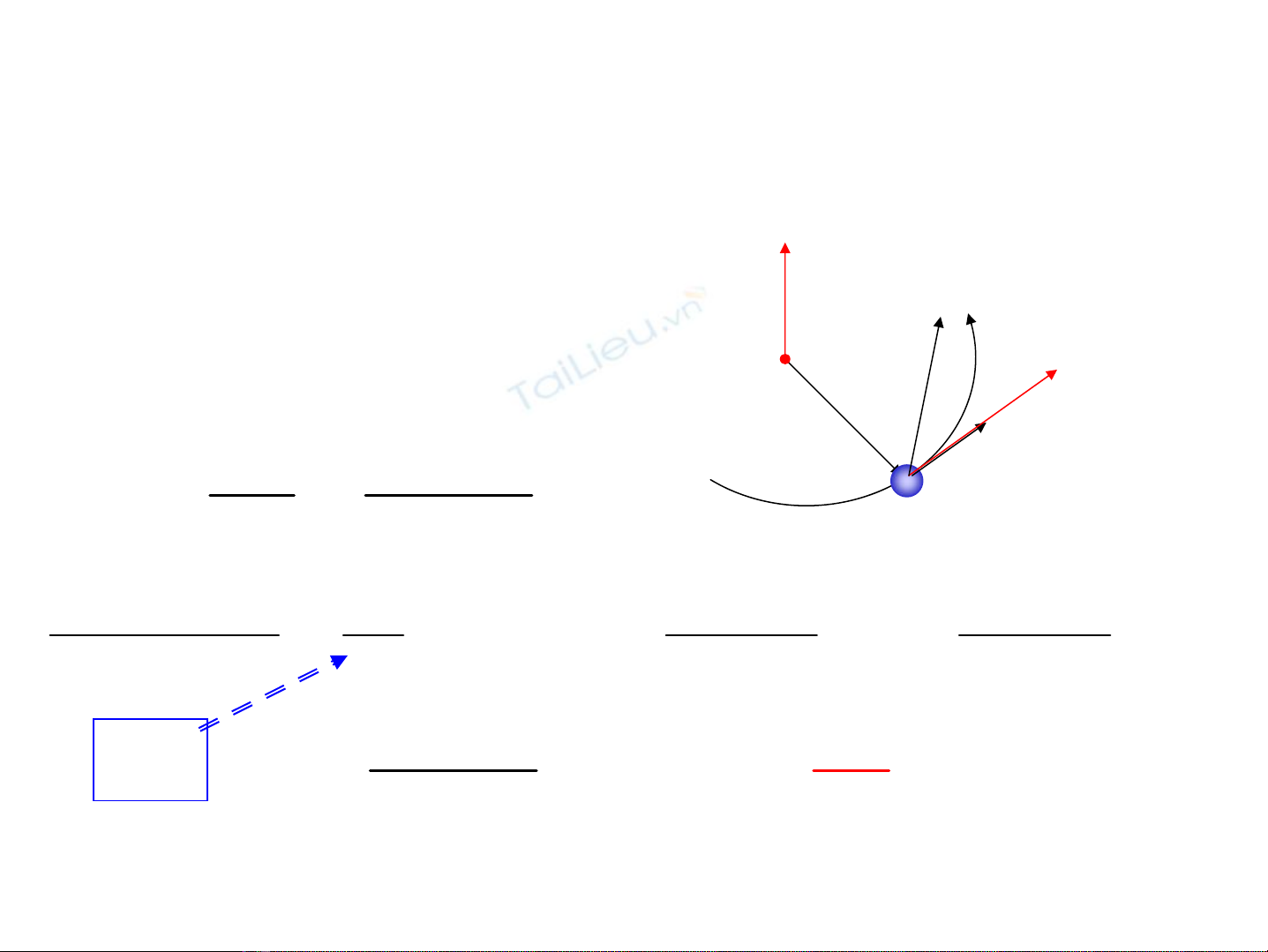
6. M«men ®éng l−îng
6.1. §Þnh nghÜa m«men ®éng l−îng cña chÊt
®iÓm chuyÓn ®éng so víi 1 ®iÓm
O
r
r
v
r
L
r
vmK
r
r
=
vmrKrL
r
r
r
r
r
×=×=
6.2.§Þnh lý vÒ m«men ®éng
l−îng
)F(
dt
Ld o/
r
r
r
μ=
F
dt
)vm(d
dt
Kd r
r
r
==
dt
)vm(d
r
dt
)vm(d
rvm
dt
rd
dt
)vmr(d
r
r
r
r
r
r
r
r
×=×+×=
×
Fr
dt
)vm(d
r
r
r
r
r×=×
Fr)F(
o/
r
r
r
r×=μ
F
r
m«men cña lùc ®èi víi O
F
r
Tam diÖn thuËn
= O
v&rL
r
r
r
⊥
HÖ qu¶: §Þnh luËt b¶o toμn m«men ®éng l−îng
cña chÊt ®iÓm 0
dt
Ld
0)F(
o/ =⇒=μ
r
r
r
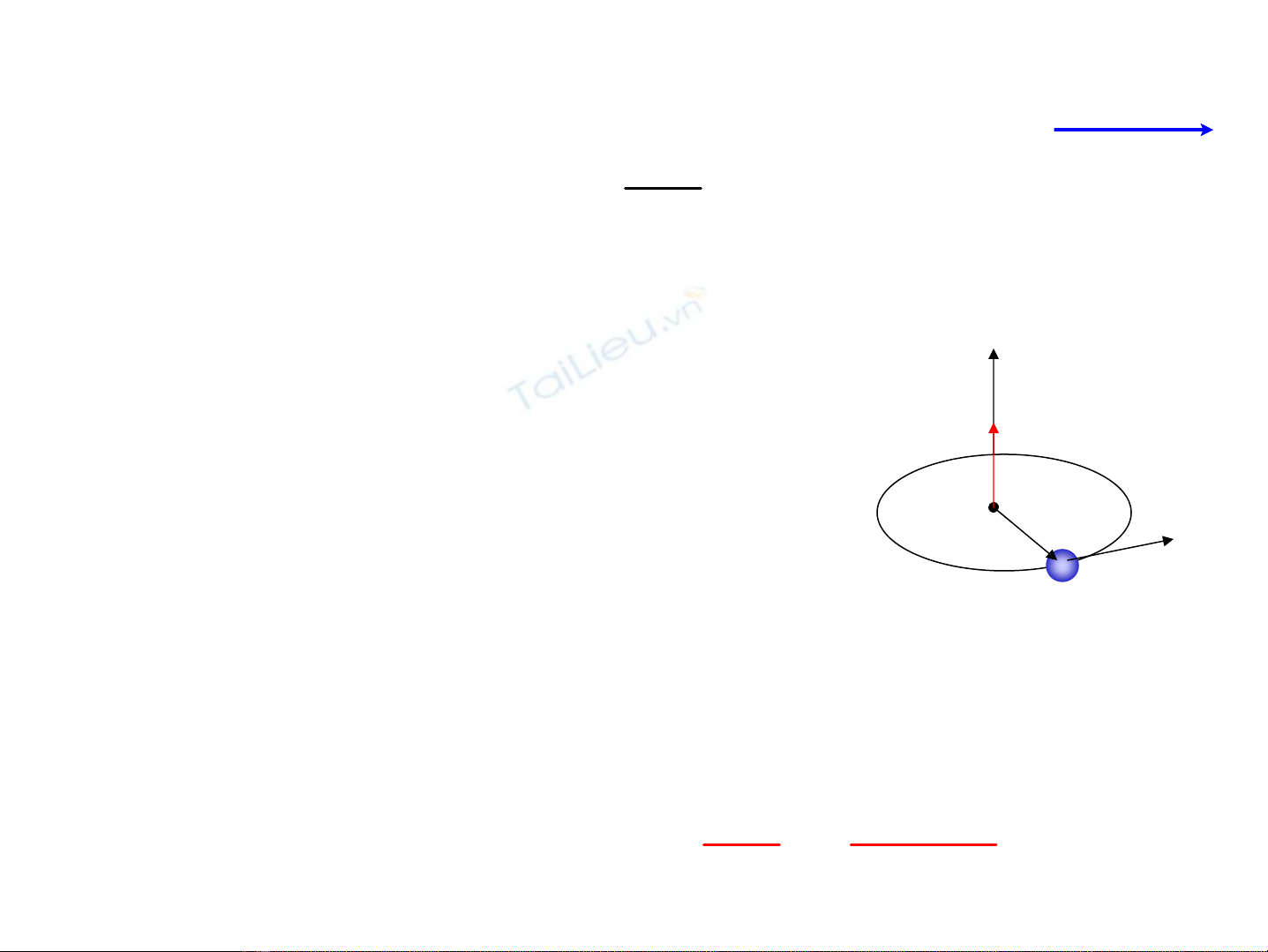
¾ChÊt ®iÓm chuyÓn ®éng trªn mÆt ph¼ng cè ®Þnh
Tr−êng hîp chuyÓn ®éng trßn L
r
ω=×= 2
mRmvR|L|
r
ImR2
=
m«men qu¸n tÝnh cña chÊt ®iÓm
®èi víi O
R
r
v
r
m
O
ω
IL
ω=
r
r
IL
nt FFF
r
r
r
+= 0)F( no/ =μ
r
r
)F(
dt
)I(d
dt
Ld tO/
r
r
r
r
μ=
ω
=
ω
r
constL =⇒
r