Bài t p Ch ng 3 – X lý song song và phân tánậ ươ ử
Câu 3 .1 : Xác đ nh s ph thu c d li u c a các l nh trong chu trình sauị ự ụ ộ ữ ệ ủ ệ :
Do i = 1 to N
S1: e[i] = x[i] – z[i];
S2: a[i+1] = e[i] + 2*d[i];
S3: a[i] = e[i];
End
DEF(S1) = {e[i]}; USE(S1) = {x[i], z[i]}
DEF(S2) = {a[i+1]}; USE(S2) = {e[i], d[i]}
DEF(S3) = {a[i]}; USE(S3) = {e[i]}
Ph thu c dòng d li u:ụ ộ ữ ệ
DEF(S1) ∩ USE(S2) ≠ Ø
DEF(S1) ∩ USE(S3) ≠ Ø
Ph thu c d li u ra:ụ ộ ữ ệ
DEF(S2) ∩ DEF(S3) ≠ Ø
Ph thu c d li u vào: ụ ộ ữ ệ
USE(S2) ∩ USE(S3) ≠ Ø
Câu 3 .2 : Hai chu trình sau có t ng đ ng v n i d ng tính toán hay khôngươ ươ ề ộ ụ ? Hãy bình lu nậ
v kh năng th c hi n song song c a các chu trình đó.ề ả ự ệ ủ
1. Do i = 1 to N
a[i] = a[i+1] + i;
end
2. Do i = N downto 1
a[i] = a[i+1] + i;
end
Hai chu trình trên không t ng đ ng v n i dung tính toán. Vì chu trình 1 khi tínhươ ươ ề ộ ở
a[i] b c th i không ph thu c vào giá tr a[i-1] c a b c th i-1 tr c đó. Trong khi chuở ướ ứ ụ ộ ị ủ ướ ứ ướ ở
trình 2 khi tính a[i] b c th i l i ph thu c vào giá tr a[i-1] c a b c th i-1 tr c đó.ở ướ ứ ạ ụ ộ ị ủ ướ ứ ướ
C hai chu trình trên d u có kh năng th c hi n song song, nh ng t nh n xét trên taả ề ả ự ệ ư ừ ậ
nh n th y kh năng th c hi n song song cho chu trình 1 d dàng h n so v i chu trình 2.ậ ấ ả ự ệ ễ ơ ớ
Hoàng Tr n Thy Ng cầ ọ Trang 1
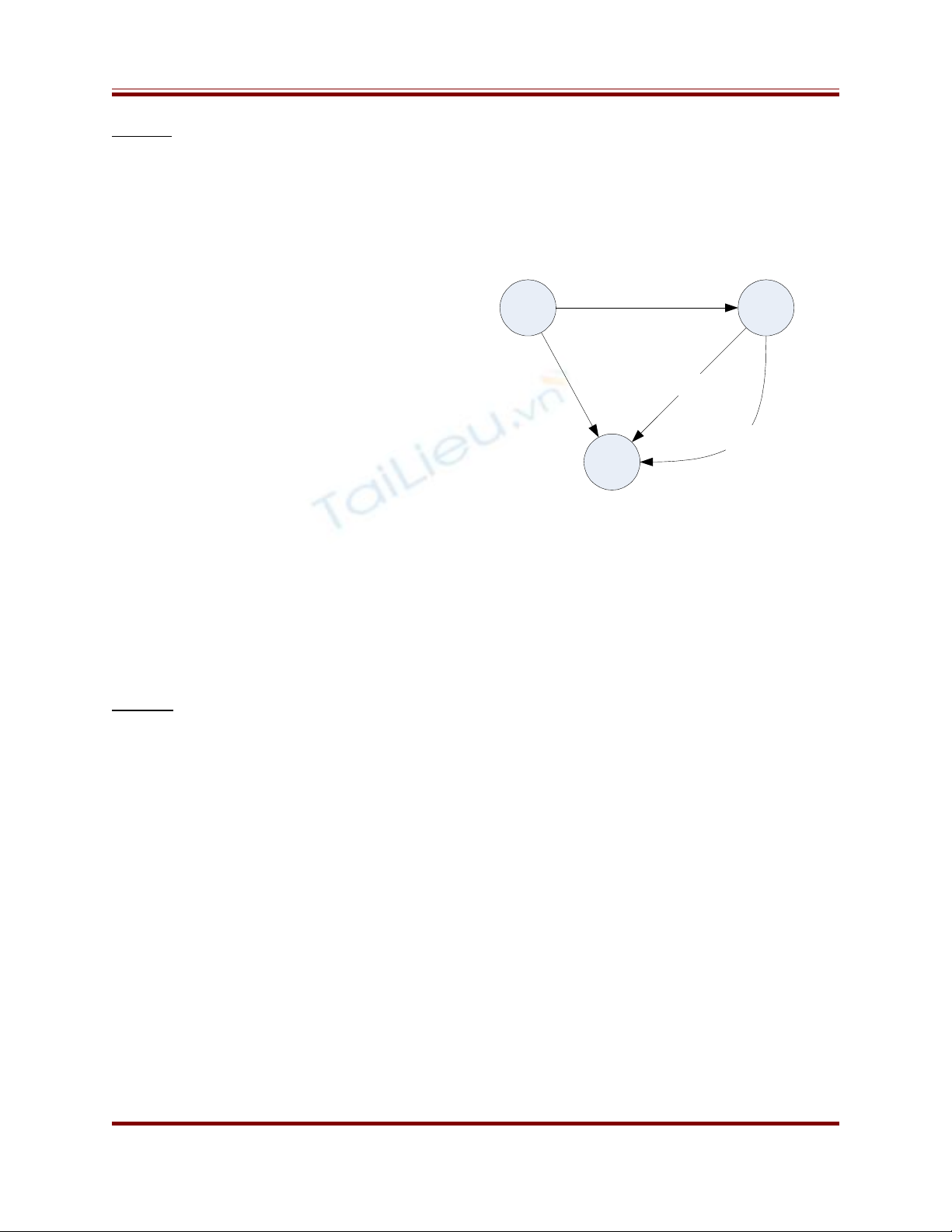
Đ th ph thu c d li uồ ị ụ ộ ữ ệ
S1
S3
S2
O
|---|
Bài t p Ch ng 3 – X lý song song và phân tánậ ươ ử
Câu 3 .3 : Xác đ nh t t c các s ph thu c d li u trong đo n ch ng trình sau:ị ấ ả ự ụ ộ ữ ệ ạ ươ
int a[Max];
read(a);
for(i = 0; i < N; i++)
for(j = 0; j < i; j++){
S1: a[i] = max(a[i], a[j]);
S2: a[j] = min(a[i], a[j]);
}
DEF(S1) = {a[i]}; USE(S1) = {a[i], a[j]}
DEF(S1) = {a[j]}; USE(S1) = {a[i], a[j]}
Ph thu c dòng d li u:ụ ộ ữ ệ
DEF(S1) ∩ USE(S2) ≠ Ø
Ph n ph thu c d li u:ả ụ ộ ữ ệ
DEF(S1) ∩ USE(S1) ≠ Ø
DEF(S2) ∩ USE(S2) ≠ Ø
DEF(S2) ∩ USE(S1) ≠ Ø
Ph thu c d li u ra: ụ ộ ữ ệ
DEF(S2) ∩ DEF (S1) ≠ Ø
Ph thu c d li u vào: ụ ộ ữ ệ
USE(S2) ∩ USE(S1) ≠ Ø
Câu 3 .4 : Lo i b các ph thu c d li u ra và ph n ph thu c d li u c a các chu trình sau.ạ ỏ ụ ộ ữ ệ ả ụ ộ ữ ệ ủ
for(i = 0; i < N; i++){
x = a[i] + b[i];
y[i] = 2 * x;
}
Chu trình trên có th đ c vi t l i nh sau đ có th lo i b ph thu c d li u và ể ượ ế ạ ư ể ể ạ ỏ ụ ộ ữ ệ ph n phả ụ
thu c d li uộ ữ ệ
for(i = 0; i < N; i++){
y[i] = 2 * (a[i] + b[i]);
}
Hoàng Tr n Thy Ng cầ ọ Trang 2
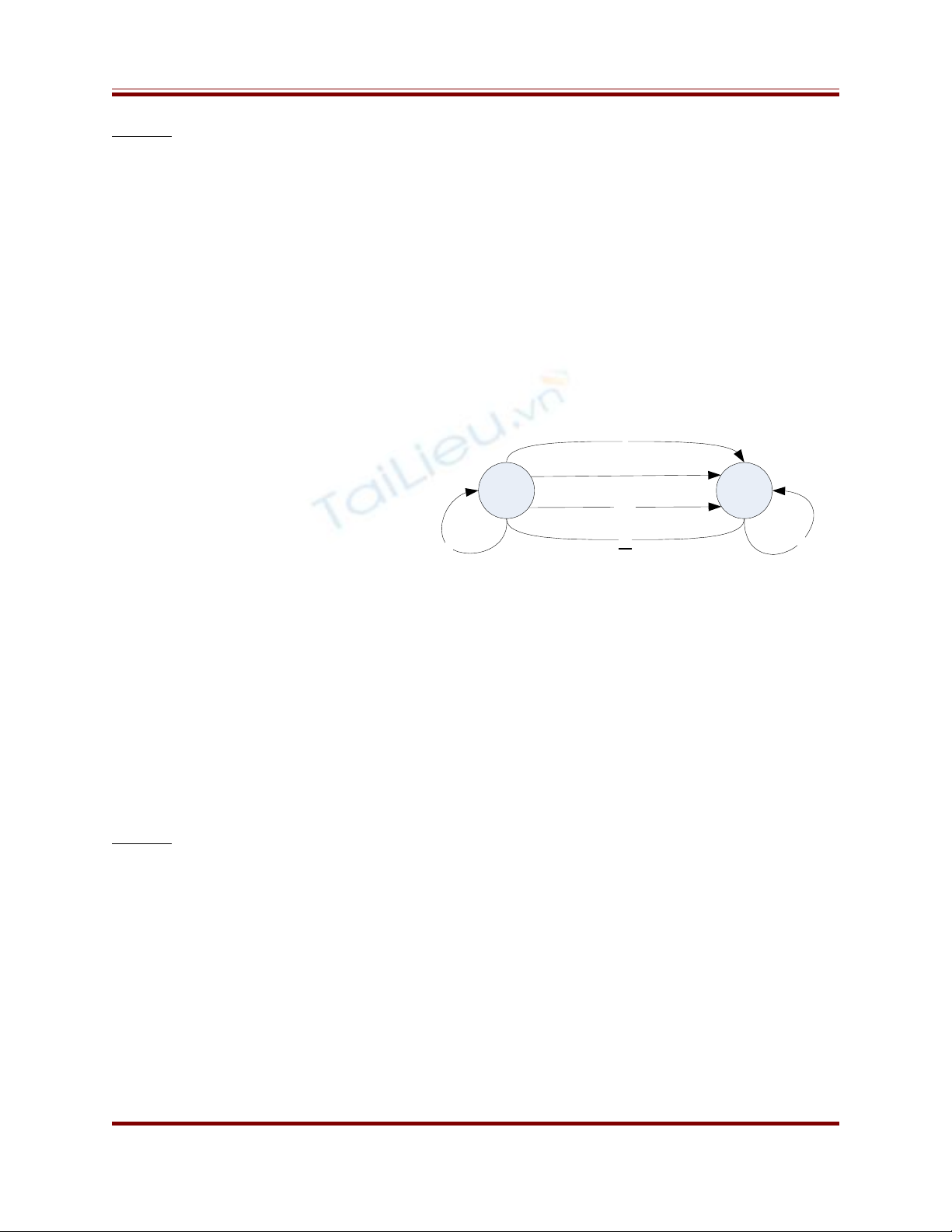
S1 S2
O
T
/\
|
Đ th ph thu c d li uồ ị ụ ộ ữ ệ
Bài t p Ch ng 3 – X lý song song và phân tánậ ươ ử
Câu 3 .5 : Phân tích đo n ch ng trình sau, xác đ nh các ph thu c d li u và v đ th phạ ươ ị ụ ộ ữ ệ ẽ ồ ị ụ
thu c d li u c a đo n ch ng trình đó.ộ ữ ệ ủ ạ ươ
S1: A = B + C;
for(i = 0; i < N; i++){
S2: D[i] = A + b[i]);
S3: S = b[i] * 5;
S4: T = T + S;
}
DEF(S1) = {A}; USE(S1) = {B, C}
DEF(S2) = {D[i]}; USE(S2) = {A, b[i]}
DEF(S3) = {S}; USE(S3) = {b[i]}
DEF(S4) = {T}; USE(S4) = {T, S}
Ph thu c dòng d li u:ụ ộ ữ ệ
DEF(S1) ∩ USE(S2) ≠ Ø
DEF(S3) ∩ USE(S4) ≠ Ø
Ph n ph thu c d li u:ả ụ ộ ữ ệ
DEF(S4) ∩ USE(S4) ≠ Ø
Ph thu c d li u vào: ụ ộ ữ ệ
USE(S3) ∩ USE(S2) ≠ Ø
Câu 3 .5 : Vi t ch ng trình gi i ph ng trình b c 2 và v đ th ph thu c d li u c a nó.ế ươ ả ươ ậ ẽ ồ ị ụ ộ ữ ệ ủ
S1: Read(a,b,c);
If (a == 0){
S2: Write(‘Day khong phai phuong trinh bac 2’);
}else{
S3: Deta = b*b - 4*a*c;
If (deta < 0){
S4: Write(‘Phuong trinh vo nghiem’);
}else{
S5: Write(‘Nghiem:’, (-b – sqrt(deta))/(2*a), (-b +
sqrt(deta))/(2*a));
}
Hoàng Tr n Thy Ng cầ ọ Trang 3
S1 S3S2
T
S4
-----
Đ th ph thu c d li uồ ị ụ ộ ữ ệ
Bài t p Ch ng 3 – X lý song song và phân tánậ ươ ử
}
DEF(S1) = {a, b, c}; USE(S1) = Ø
DEF(S2) = Ø; USE(S2) = Ø
DEF(S3) = {deta}; USE(S3) = {a, b, c}
DEF(S4) = Ø; USE(S4) = Ø
DEF(S5) = Ø; USE(S5) = {deta, a, b, c}
Ph thu c dòng d li u:ụ ộ ữ ệ
DEF(S1) ∩ USE(S3) ≠ Ø
DEF(S1) ∩ USE(S5) ≠ Ø
DEF(S3) ∩ USE(S5) ≠ Ø
Ph thu c d li u vào: ụ ộ ữ ệ
USE(S5) ∩ USE(S3) ≠ Ø
Ph thu c đi u khi n d li u: ụ ộ ề ể ữ ệ
S2, S3 ph thu c vào S1ụ ộ
S4, S5 ph thu c vào S3ụ ộ
Hoàng Tr n Thy Ng cầ ọ Trang 4
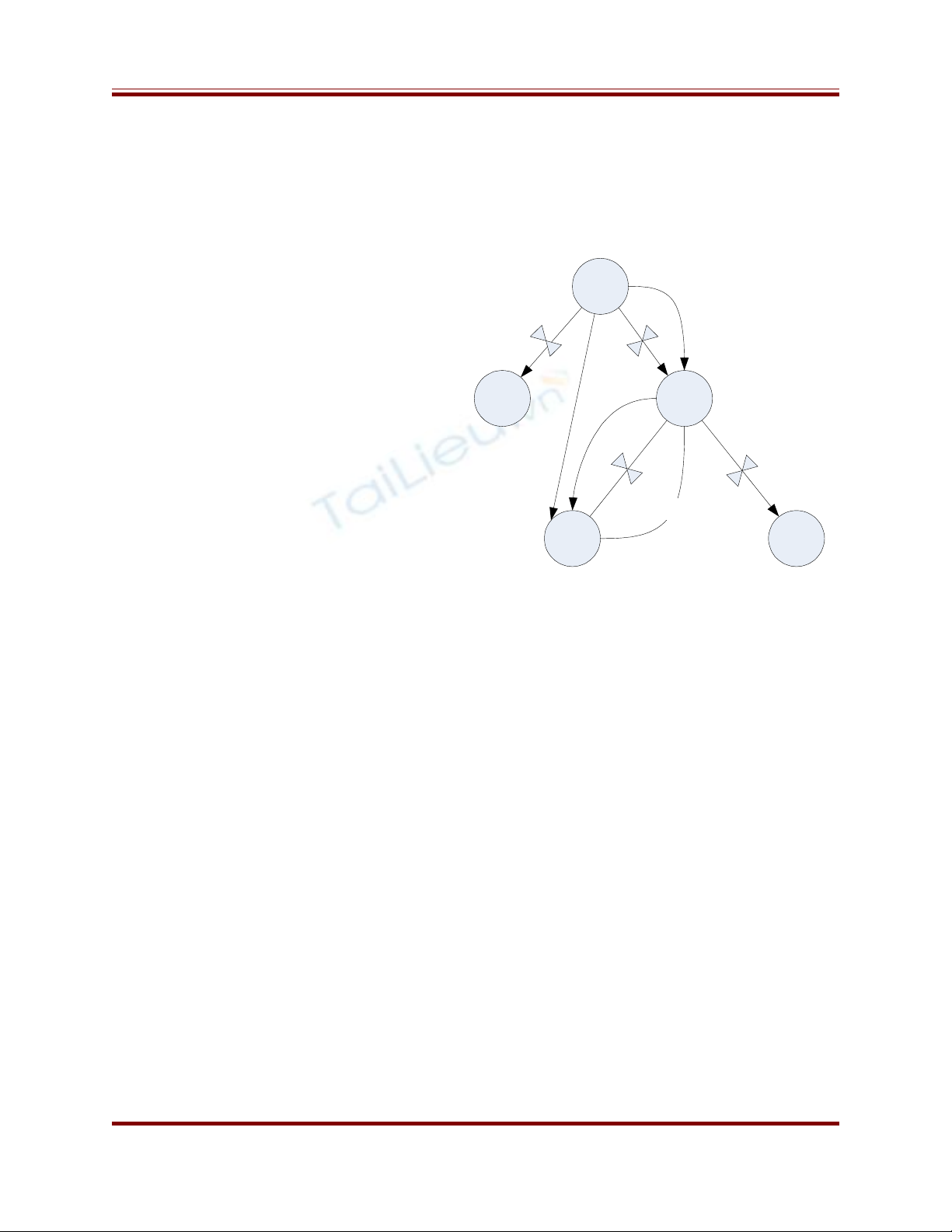
Đ th ph thu c d li uồ ị ụ ộ ữ ệ
S1
S3S2
S4S5
|----|