DSP NTrD
X LÝ TÍN HI U SỬ Ệ Ố
Tài li u tham kh o chính:ệ ả
1.Nguy n Qu c Trung: ễ ố X lý tín hi u s NXB ử ệ ố
Giáo d c 2001 (2 t p)ụ ậ
2.T ng Văn On: ốLý thuy t và bài t p X lý tín ế ậ ử
hi u sệ ố
3.D ng T C ng: ươ ử ườ X lý tín hi u sử ệ ố
4.Tài li u Digital Signal Proccessing truy c p trên ệ ậ
m ngạ
02/09/13 1
I. T ng quan v tín hi u và h th ng x lý tín ổ ề ệ ệ ố ử
hi uệ
II. H th ng TGRR đ c mô t b ng PTSPệ ố ượ ả ằ
III. Bi n đ i Z và ng d ngế ổ ứ ụ
IV. Bi n đ i Fourier và ng d ngế ổ ứ ụ
V. Các b l c sộ ọ ố
DSP NTrD 02/09/13 2
1. Signal classification
Tín hi u là đ nh l ng v t lý c a m t đ i l ng ệ ị ượ ậ ủ ộ ạ ượ
bi n đ i theo th i gian ho c theo không gian, d i ế ổ ờ ặ ướ
d ng tín hi u t ng t (Analog) ho c d ng s ạ ệ ươ ự ặ ạ ố
(Digital), đ c t o ra t các ngu n khác nhau. ượ ạ ừ ồ Tín
hi u là bi u di n v t lý c a thông tinệ ể ễ ậ ủ
Trong ph m vi x lý tín hi u, các chu i d li u nh ạ ử ệ ỗ ữ ệ ị
phân không đ c coi là tín hi uượ ệ , mà ta chỉ quan
tâm đến các định lượng vật lý của các tín hiệu tương
tự biểu diễn các tín hiệu.
DSP NTrD 02/09/13 3
Đối với tín hiệu tương tự, xử lý tín hiệu có thể là các thao tác
khuyếch đại, lọc trong lĩnh vực âm tần, điều biến
(Modulation) hay giải điều biến (Demulation) các tín hiệu
trong truyền thông …
Đối với tín hiệu số, xử lý tín hiệu bao gồm các công việc như
lọc tín hiệu, nén và giải nén tín hiệu số, mã hóa, giải
mã,v.v…
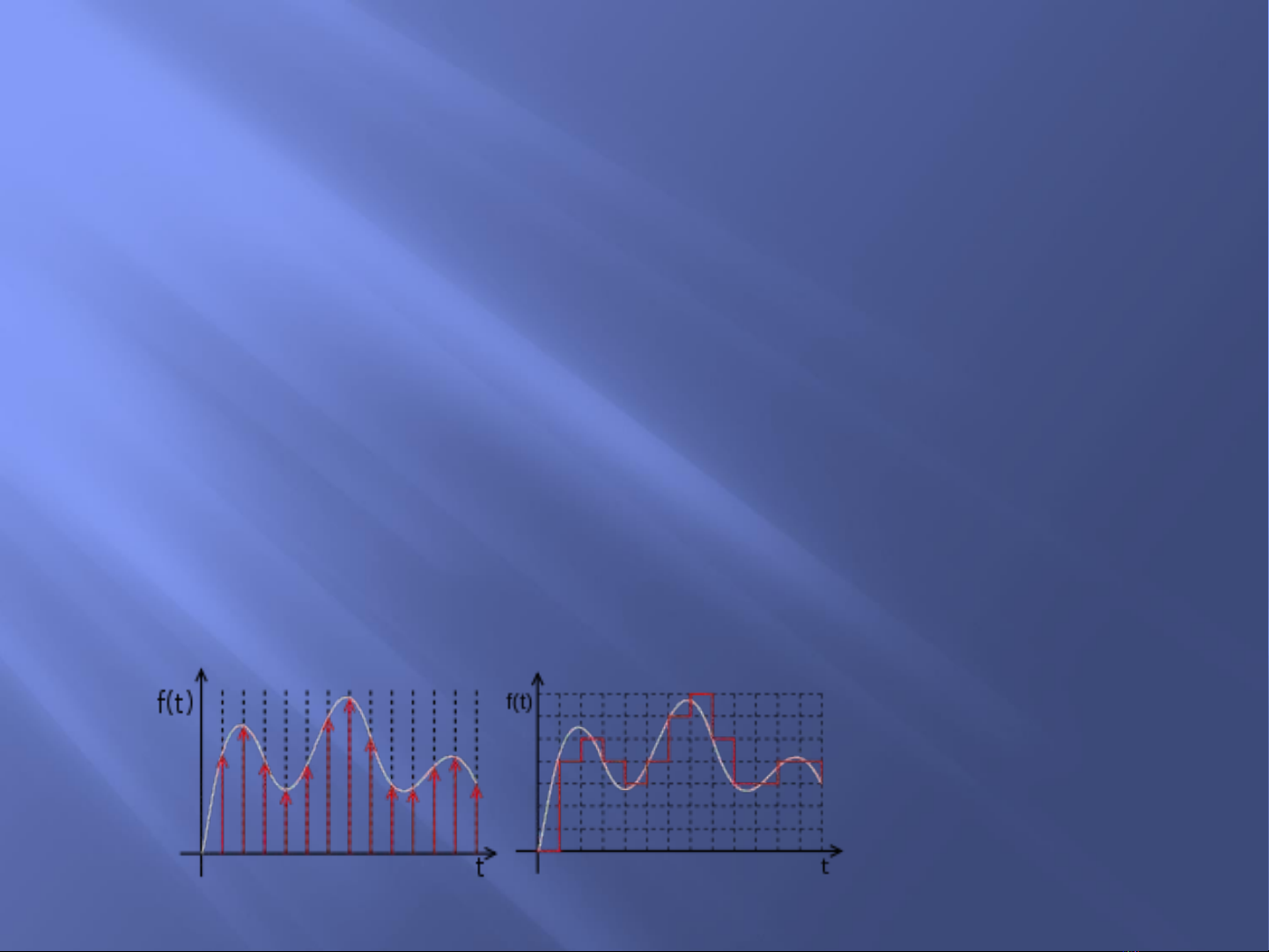
Tín hiệu rời rạc: Còn gọi là tín hiệu thời gian rời rạc, là một
chuỗi giá trị được “lấy mẫu” tại từng thời điểm của tín hiệu
liên tục.
DSP NTrD 02/09/13 4
Nếu tín hiệu thời gian rời rạc (TGRR) là một chuỗi
tương ứng với khoảng thời gian lấy mẫu đồng đều,
ta có thêm khái niệm thời gian lấy mẫu (Chu kỳ), dĩ
nhiên, chu kỳ lấy mẫu không phải là một đại lượng
đi cùng trong chuỗi tín hiệu. Chu kỳ lấy mẫu là một
đại lượng đặc trưng khác.
Tín hi u s là tín hi u TGRR ch g m t p các ệ ố ệ ỉ ồ ậ giá
trị. Đây là các giá trị được định lượng từ các tín hiệu
TGRR.
DSP NTrD 02/09/13 5