PH N 1: NGUYÊN LÝ MÁYẦ
Ch ng 1.ươ
C U TRÚC C C UẤ Ơ Ấ
1.1. NH NG KHÁI NI M C B NỮ Ệ Ơ Ả
Bài toán c u trúc c c u là nghiên c u và thi t k s đ đ ng c a c c u vàấ ơ ấ ứ ế ế ơ ồ ộ ủ ơ ấ
máy theo yêu c u chuy n đ ng c a quy trình công ngh đã cho. Đ gi i bài toánầ ể ộ ủ ệ ể ả
trên c n nghiên c u nh ng khái ni m c b n v c u t o và đ ng h c c a c c uầ ứ ữ ệ ơ ả ề ấ ạ ộ ọ ủ ơ ấ
và máy.
1.1.1. Khâu
Khâu có th là m t v t r n đ c l p, ho c là m t t p h p n i c ng c a m tể ộ ậ ắ ộ ậ ặ ộ ậ ợ ố ứ ủ ộ
s v t r n có cùng chung m t d ng chuy n đ ng.ố ậ ắ ộ ạ ể ộ
1.1.2. B c t do c a v t r nậ ự ủ ậ ắ
B c t do c a v t r n là s kh năng chuy n đ ng đ c l p, hay là s thôngậ ự ủ ậ ắ ố ả ể ộ ộ ậ ố
s đ c l p c n đ xác đ nh v trí c a v t r n.ố ộ ậ ầ ể ị ị ủ ậ ắ
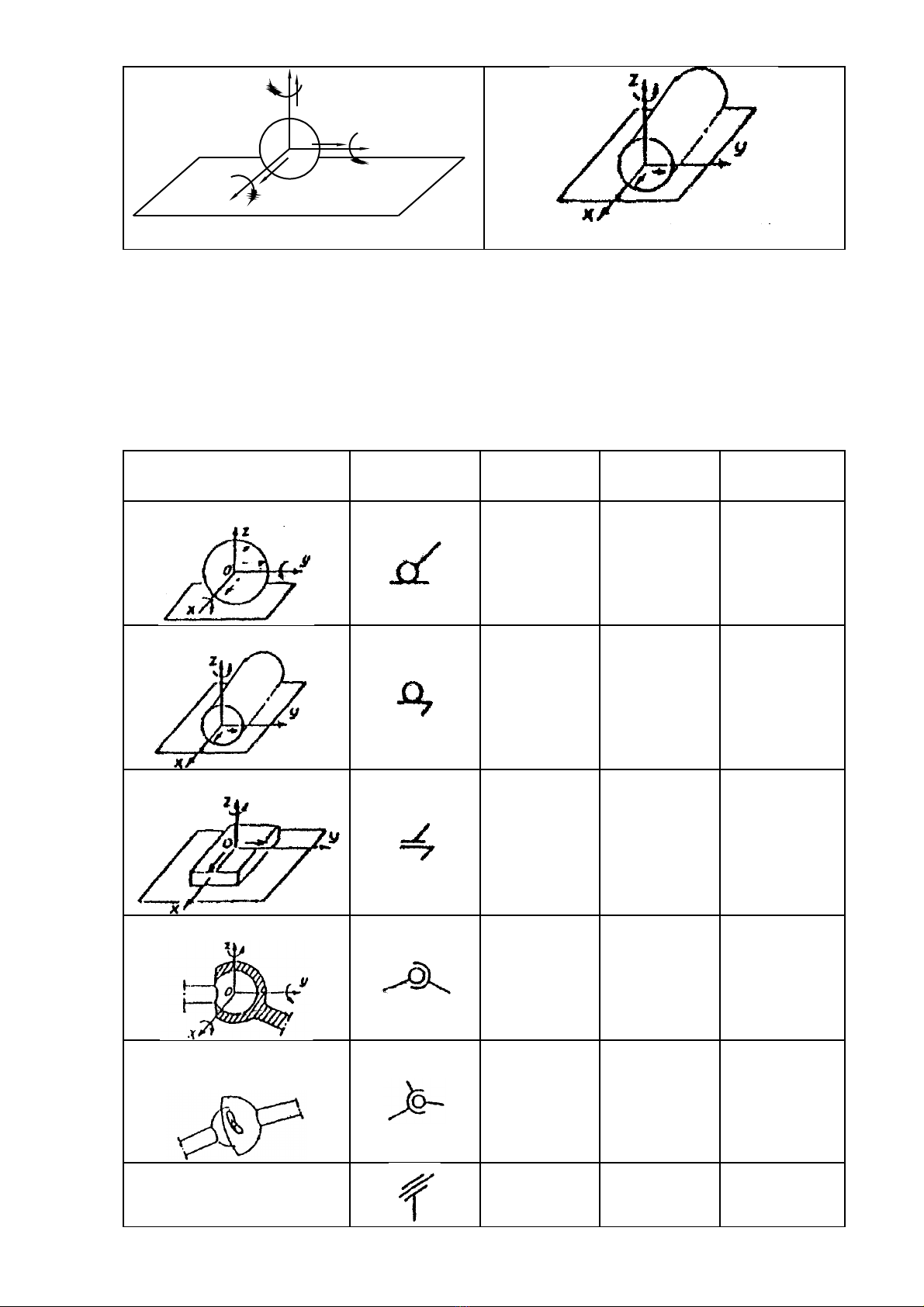
Xét m t v t r n S chuy n đ ng trong m t ph ng xoy (hình 1.1a). Nó có baộ ậ ắ ể ộ ặ ẳ
kh năng chuy n đ ng đ ng l p:ả ể ộ ộ ậ
S
T
Tx
y
y
z
x
o
z
Q
a)
Qz
ox
z
y
y
x
T
T
S
x
Q
Tz
Qy
b)
Hình 1.1. B c t do c a v t r nậ ự ủ ậ ắ
- Hai chuy n đ ng t nh ti n ể ộ ị ế
x
T
và
y
T
d c theo hai tr c ox và oy t o nên m tọ ụ ạ ặ
ph ng chuy n đ ng.ẳ ể ộ
- M t chuy n đ ng quay quanh tr c oz là ộ ể ộ ụ
z
Q
vuông góc v i m t ph ngớ ặ ẳ
chuy n đ ng c a S. Vì v y trong m t m t ph ng v t r n có ba kh năng chuy nể ộ ủ ậ ộ ặ ẳ ậ ắ ả ể
đ ng đ c l p (ba b c t do): ộ ộ ậ ậ ự
x
T
,
y
T
và
z
Q
.
Trong không gian (hình 1.1b) v t r n S có sáu b c t do: ậ ắ ậ ự
x
T
,
y
T
,
z
T
và
x
Q
,
y
Q
,
z
Q
.
1.1.3. N i đ ng và kh p đ ngố ộ ớ ộ
N i đ ng là m i n i hai khâu nh ng gi a chúng v n chuy n đ ng t ng đ iố ộ ố ố ư ữ ẫ ể ộ ươ ố
v i nhau. M i n i g a hai khâu đ ng v i nhau g i là kh p đ ng. B ph n hai khâuớ ố ố ữ ộ ớ ọ ớ ộ ộ ậ
ti p xúc v i nhau g i là thành ph n kh p đ ng, nó có th là đi m, đ ng ho cế ớ ọ ầ ớ ộ ể ể ườ ặ
m t.ặ
Theo thành ph n kh p đ ng ng i ta phân lo i: ầ ớ ộ ườ ạ
- Kh p lo i cao (kh p cao hay kh p lo i 1 và lo i 2) là kh p ti p xúc gi aớ ạ ớ ớ ạ ạ ớ ế ữ
hai khâu theo đi m ho c theo đ ng (di n tích ti p xúc b ng 0). (Hình 1.2).ể ặ ườ ệ ế ằ
- Kh p lo i th p (kh p th p) là kh p ti p xúc gi a hai khâu là m t. Nó g mớ ạ ấ ớ ấ ớ ế ữ ặ ồ
kh p lo i 3 đ n lo i 5.ớ ạ ế ạ
1
y
Q
z
TQx
T
Tx
y
y
z
x
o
z
Q
a) b)
Hình 1.2. Kh p lo i caoớ ạ
a. C u và m t ph ng (ti p xúc đi m); b. Tr và m t ph ng (ti p xúc đ ng)ầ ặ ẳ ế ể ụ ặ ẳ ế ườ
Theo s b c t do b h n ch do kh p t o đ c đ h n ch kh năng chuy nố ậ ự ị ạ ế ớ ạ ượ ể ạ ế ả ể
đ ng c a khâu này so v i khâu kia ng i ta phân lo i kh p t lo i 1 đ n lo i 5. Độ ủ ớ ườ ạ ớ ừ ạ ế ạ ể
thu n ti n cho vi c nghiên c u và thi t k ng i ta dùng các l c đ kh p đ ngậ ệ ệ ứ ế ế ườ ượ ồ ớ ộ
(b ng 1.1).ả
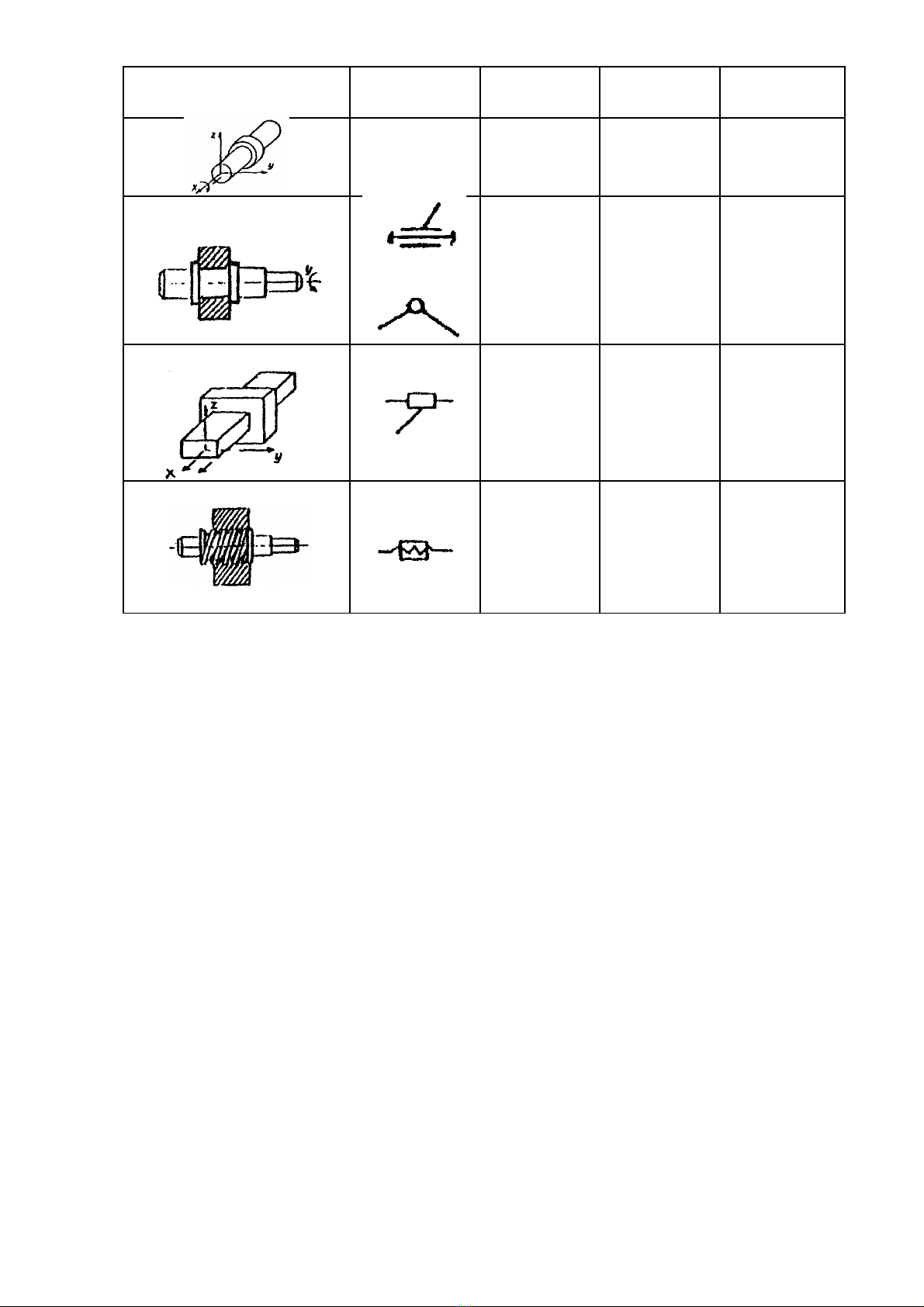
B ng 1.1. L c đ kh p đ ngả ượ ồ ớ ộ
Kh p đ ngớ ộ L c đượ ồ B c t doậ ự
h n chạ ế B c t doậ ự
còn l iạKh p lo iớ ạ
Qu c u – m t ph ngả ầ ặ ẳ
1 5 1
Hình tr - m t ph ngụ ặ ẳ
2 4 2
Hình h p – m t ph ngộ ặ ẳ
3 3 3
Kh p c uớ ầ
3 3 3
Kh p c u – ch tớ ầ ố
4 2 4
Kh p trớ ụ 4 2 4
2
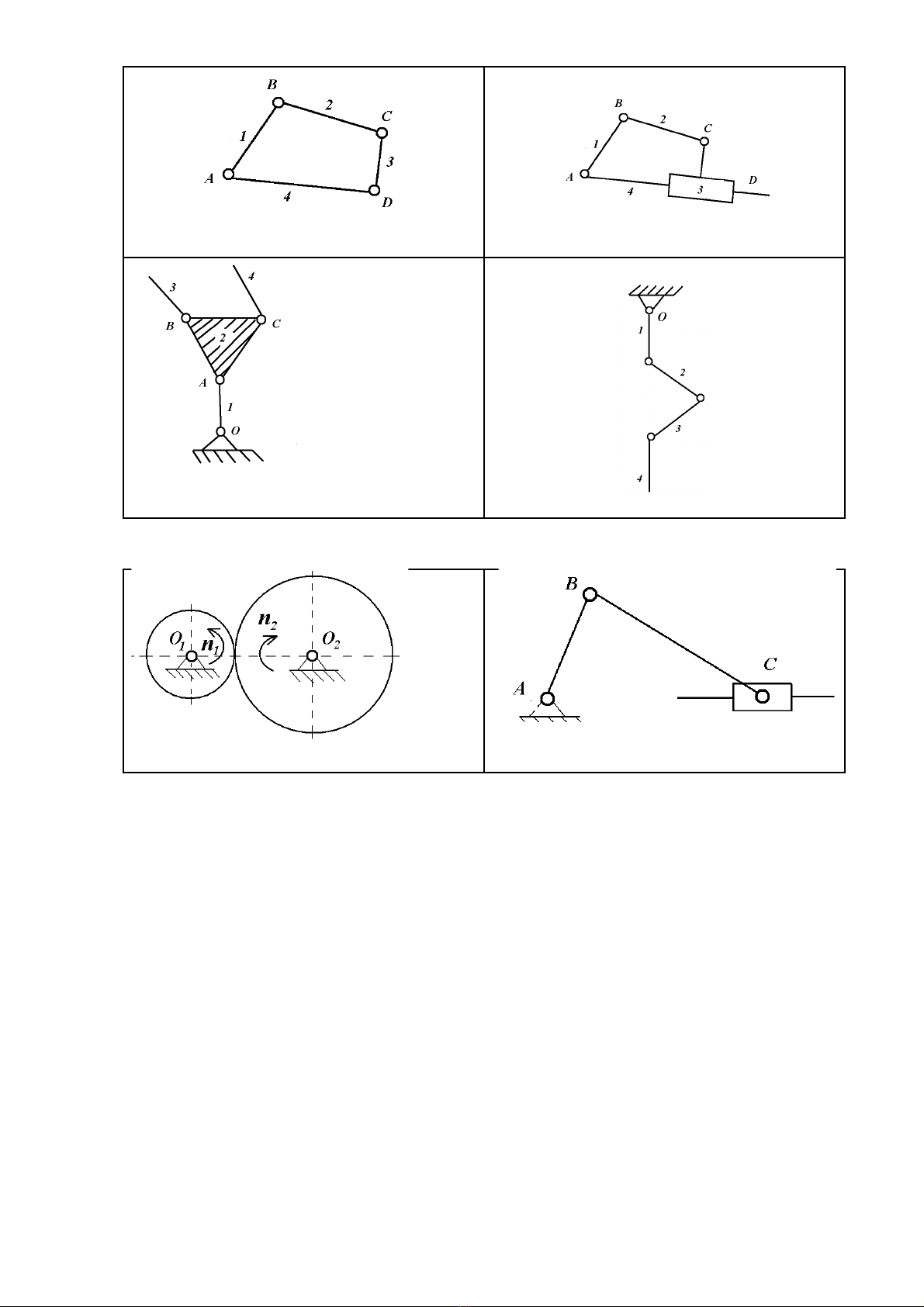
Kh p đ ngớ ộ L c đượ ồ B c t doậ ự
h n chạ ế B c t doậ ự
còn l iạKh p lo iớ ạ
Kh p quayớ
5 1 5
Kh p t nh ti nớ ị ế
5 1 5
Kh p vítớ
5 1 5
1.1.4. Chu i đ ngỗ ộ
Chu i đ ng là t p h p các khâu n i v i nhau b ng kh p đ ng. Nó đ c chiaỗ ộ ậ ợ ố ớ ằ ớ ộ ượ
thành:
a. Chu i đ ng đ n gi n và ph c t pỗ ộ ơ ả ứ ạ
- Chu i đ ng đ n gi n: các khâu không tham gia quá hai kh p (hìnhỗ ộ ơ ả ớ
1.3a,b,d).
- Chu i đ ng ph c t p: có khâu tham gia t ba kh p tr lên (hình1.3.c).ỗ ộ ứ ạ ừ ớ ở
b. Chu i đ ng kín và chu i đ ng hỗ ộ ỗ ộ ở
- Chu i đ ng kín: các khâu tham gia ít nh t hai kh p (hình 1.3a,b).ỗ ộ ấ ớ
- Chu i đ ng h : có khâu tham gia ch 1 kh p (hình1.3. c, d).ỗ ộ ở ỉ ớ
c. Chu i đ ng ph ng và chu i đ ng không gianỗ ộ ẳ ỗ ộ
Trong chu i đ ng ph ng các khâu ch chuy n đ ng trên m t m t ph ngỗ ộ ẳ ỉ ể ộ ộ ặ ẳ
ho c trên các m t song song v i nhau.ặ ặ ớ
Trong chu i đ ng không gian các khâu chuy n đ ng trên các m t ph ngỗ ộ ể ộ ặ ẳ
khác nhau, không song song v i nhau.ớ
1.2. C C U VÀ MÁYƠ Ấ
1.2.1. C c uơ ấ
C c u là chu i đ ng kín có m t khâu c đ nh (khâu c đ nh g i là giá). Xétơ ấ ỗ ộ ộ ố ị ố ị ọ
v m t công d ng, c c u là t h p nhân t o m t s khâu có chuy n đ ng xácề ặ ụ ơ ấ ổ ợ ạ ộ ố ể ộ
đ nh dùng đ truy n ho c bi n đ i chuy n đ ng. Có hai lo i c c u:ị ể ề ặ ế ổ ể ộ ạ ơ ấ
- C c u dùng đ truy n chuy n đ ng: chuy n đ ng truy n t khâu nàyơ ấ ể ề ể ộ ể ộ ề ừ
sang khâu khác d ng chuy n đ ng không thay đ i, nh c c u bánh răng (hìnhạ ể ộ ổ ư ơ ấ
1.4a).
- C c u dùng đ bi n đ i chuy n đ ng: d ng chuy n đ ng thay đ i khiơ ấ ể ế ổ ể ộ ạ ể ộ ổ
truy n t khâu này sang khâu khác, nh c c u tay quay con tr t (hình 1.4b).ề ừ ư ơ ấ ượ
3
a) b)
c) d)
Hình 1.3. Chu i đ ngỗ ộ
a) C c u bánh răngơ ấ b) C c u tay quay con tr tơ ấ ượ
Hình 1.4. C c uơ ấ
1.2.2. Máy
Máy là t h p nhân t o t m t s c c u và m t s ph tùng khác cóổ ợ ạ ừ ộ ố ơ ấ ộ ố ụ
chuy n đ ng xác đ nh, khi s d ng năng l ng s sinh ra công có ích. Máy đ cể ộ ị ử ụ ượ ẽ ượ
chia làm ba lo i nh sau:ạ ư
- Máy năng l ng: các lo i đ ng c s d ng năng l ng và các lo i máyượ ạ ộ ơ ử ụ ượ ạ
phát s n sinh ra năng l ng.ả ượ
- Máy công tác: các máy th ng dùng trong các ngành công nghi p: máyườ ệ
b m, máy v n t i, máy khai thác,…trong các máy công tác bao g m máy năngơ ậ ả ồ
l ng.ượ
- Các lo i máy khác: kính hi n vi, các lo i máy thu phát sóng vô tuy n…ạ ể ạ ế
1.3. B C T DO C A C C UẬ Ự Ủ Ơ Ấ
B c t do c a c c u là s kh năng chuy n đ ng đ c l p c n đ xác đ nhậ ự ủ ơ ấ ố ả ể ộ ộ ậ ầ ể ị
v trí c c u.ị ơ ấ
1.3.1. B c t do c a c c u ph ngậ ự ủ ơ ấ ẳ
Trong m t ph ng gi s có n khâu đ ng đ c n i v i nhau b ng các kh pặ ẳ ả ử ộ ượ ố ớ ằ ớ
th p (ấ
) và kh p cao (ớ
c
P
), theo P.L. Trêb sep (nhà bác h c ng i Nga 1821-1894),ư ọ ườ
s b c t do (W) c a c c u đ c xác đ nh:ố ậ ự ủ ơ ấ ượ ị
4
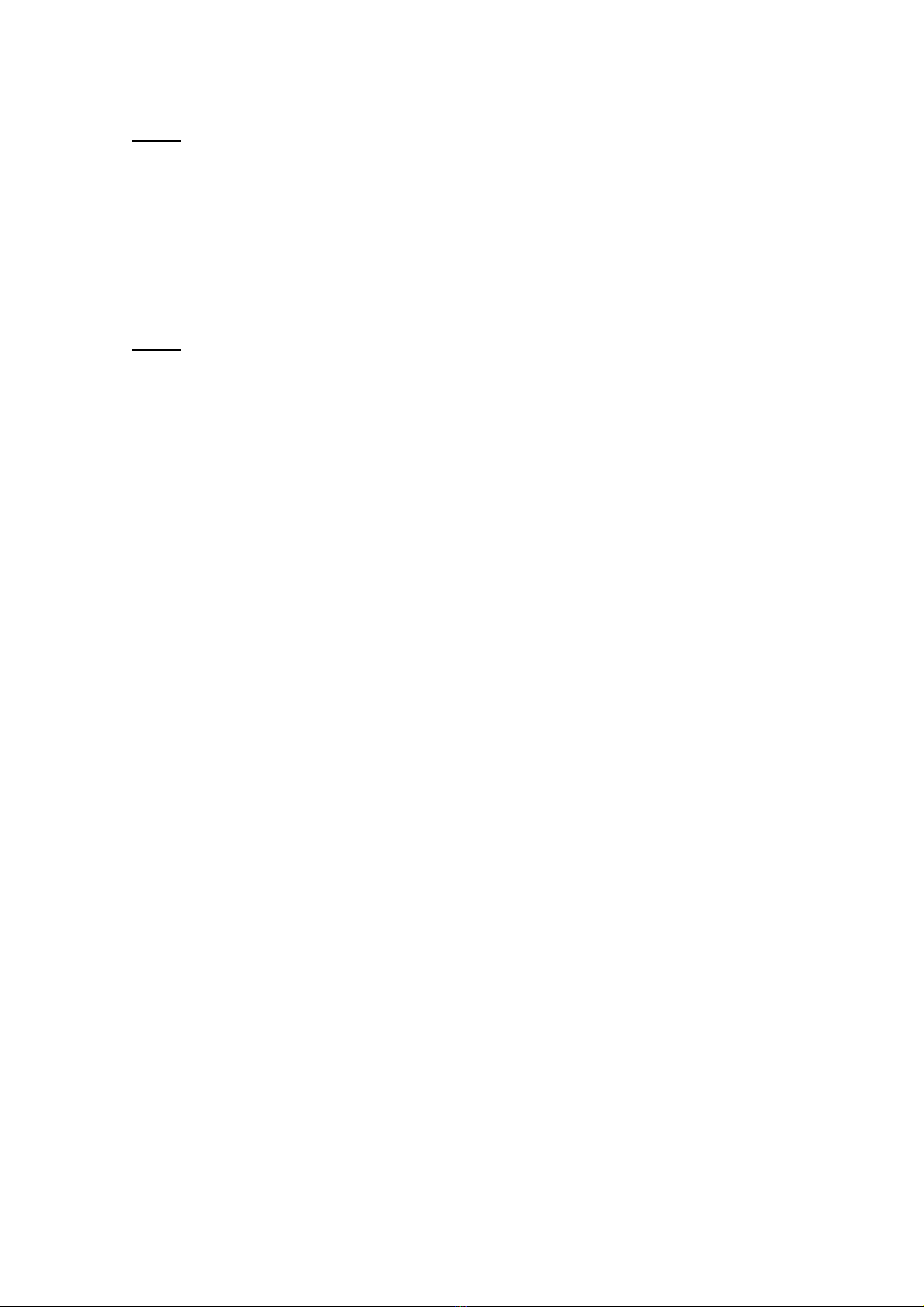
ct
ppnW −−= .2.3
(1.1)
Ví d 1.1. Xác đ nh s b c t do c a c c u bánh răng cho hình 1.4a.ụ ị ố ậ ự ủ ơ ấ ở
Gi i:ả
Đây là c c u ph ng, có:ơ ấ ẳ
n = 2 (hai bánh răng ăn kh p v i nhau) ớ ớ
= 2 ( hai kh p Oớ1 và O2 là hai kh p b n l ti p xúc v i nhau là ti p xúcớ ả ề ế ớ ế
m t)ặ
c
P
= 1 (ti p đi m c a hai vòng lăn là ti p xúc đ ng)ế ể ủ ế ườ
11.12.22.3.2.3 =−−=−−= ct ppnW
Ví d 1.2. Xác đ nh s b c t do c a c c u tay quay con tr t cho hình 1.4b.ụ ị ố ậ ự ủ ơ ấ ượ ở
Gi i:ả
Đây là c c u ph ng, có:ơ ấ ẳ
n = 3 (có ba khâu là AB, BC và con tr t) ượ
= 4 ( ba kh p b n l và m t kh p tr t ti p xúc v i nhau là ti p xúc m t)ớ ả ề ộ ớ ượ ế ớ ế ặ
c
P
= 0 (không có kh p nào là ti p xúc đ ng)ớ ế ườ
10.14.23.3.2.3 =−−=−−= ct ppnW
1.3.2. B c t do c a c c u không gianậ ự ủ ơ ấ
Trong không gian, gi s c c u có n khâu đ ng s có 6.n b c t do khiả ử ơ ấ ộ ẽ ậ ự
ch a n i chúng v i nhau. ư ố ớ
T ng quát trong c c u có:ổ ơ ấ P1 kh p lo i 1 (h n ch đ c m t b c t do)ớ ạ ạ ế ượ ộ ậ ự
P2-----------2 (h n ch đ c hai b c t do)ạ ế ượ ậ ự
P3-----------3 (h n ch đ c ba b c t do)ạ ế ượ ậ ự
P4-----------4 (h n ch đ c b n b c t do)ạ ế ượ ố ậ ự
P5-----------5 (h n ch đ c năm b c t do)ạ ế ượ ậ ự
Thì s b c t do c a c c u s là:ố ậ ự ủ ơ ấ ẽ
).1.2.3.4.5(.6 12345 PPPPPnW ++++−=
(1.2)
1.3.3. B c t do th a, ràng bu c th a.ậ ự ừ ộ ừ
M t s c u trúc đ c bi t nh h ng đ n b c t do c a c c u. Trongộ ố ấ ặ ệ ả ưở ế ậ ự ủ ơ ấ
nh ng tr ng h p nh v y c n ph i chú ý khi áp d ng các công th c ( 1.1) vàữ ườ ợ ư ậ ầ ả ụ ứ
(1.2) đ tính b c t do c a c c u.ể ậ ự ủ ơ ấ
Xét m t s tr ng h p sau:ộ ố ườ ợ
Xét c c u cam (H 1.5) g m có 3 khâu đ ng, 3 kh p th p (A, B, C) và m tơ ấ ồ ộ ớ ấ ộ
kh p cao (kh p gi a cam 1 và con lăn 2). Áp d ng công th c (1.1), ta có:ớ ớ ữ ụ ứ
21.13.23.3
=−−=
W
Trong tr ng h p này con lăn 2 là khâu th a. Th c v y, tính ch t chuy nườ ợ ừ ự ậ ấ ể
đ ng c a c c u này không đ i n u ta tăng bán kính cam 1 lên m t đ i l ng rộ ủ ơ ấ ổ ế ộ ạ ượ
b ng bán kính con lăn 2 thì kh p cao s là tâm con lăn B.ằ ớ ẽ
Xét c c u v hình elip (H 1.6) g m 4 khâu đ ng n i v i nhau b ng 6 kh pơ ấ ẽ ồ ộ ố ớ ằ ớ
th p. Theo công th c (1.1) b c t do c a nó s là:ấ ứ ậ ự ủ ẽ
00.16.24.3 =−−=W
Nh ng th c t c c u này có W = 1. Trong c c u này có AB = BC = BD vàư ự ế ơ ấ ơ ấ
góc CAD = 900, khâu AB là khâu th a có ừ
12.21.3
−=−=
W
(1 khâu và 2 kh p th p Aớ ấ
và B).
Mu n xác đ nh b c t do th a ho c ràng bu c th a ph i phân tích k đ cố ị ậ ự ừ ặ ộ ừ ả ỹ ặ
bi t chuy n đ ng c a c c u.ệ ể ộ ủ ơ ấ
5