Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 12
12/14/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 6 Tính biếndạng của thanh
2. Thanh chịuxoắnthuầntúy
NỘIDUNG
3. Thanh chịuuốn ngang phẳng
1. Thanh chịukéonénđúng tâm
CHƯƠNG 6 Tính biếndạng của thanh
1. Thanh chịukéonénđúng tâm
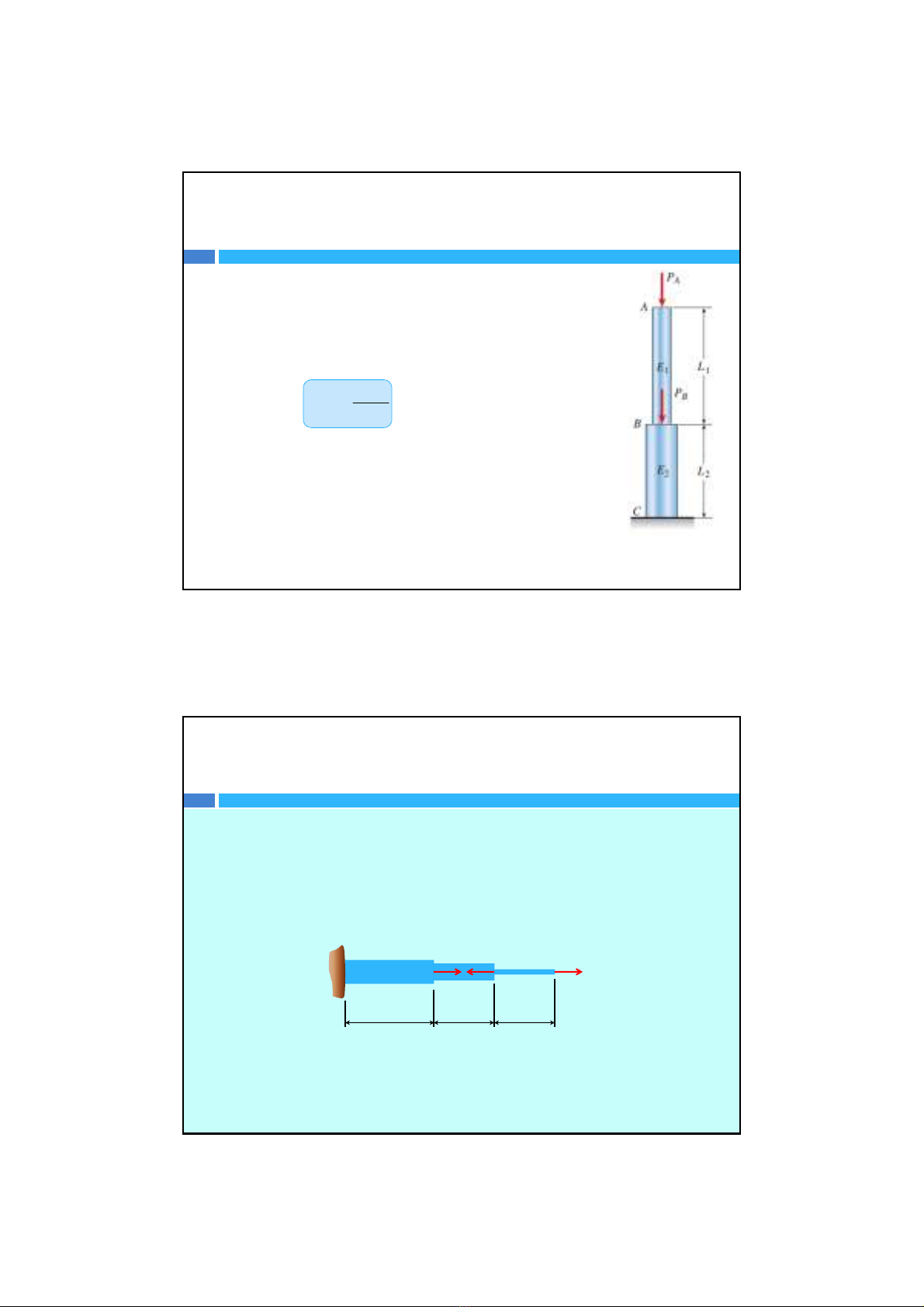
Xét thanh đồng nhấtBCcóchiều dài L và diệntíchcủamặt
cắtngangkhôngđổilàAchịulựckéođúng tâm là P.
Ta tính đượcứng suất trong thanh là
P
A
Mà theo định luật Hooke ta được
E
P
EEA

Theo định nghĩatađượcbiếndạng tỉđốilàtỉsốbiếndạng tuyệtđốivà
chiều dài thanh.
L
Vì thế,tađượcbiếndạng tuyệtđối
L
P
L
EA

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 12
12/14/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 6 Tính biếndạng của thanh
1. Thanh chịukéonénđúng tâm
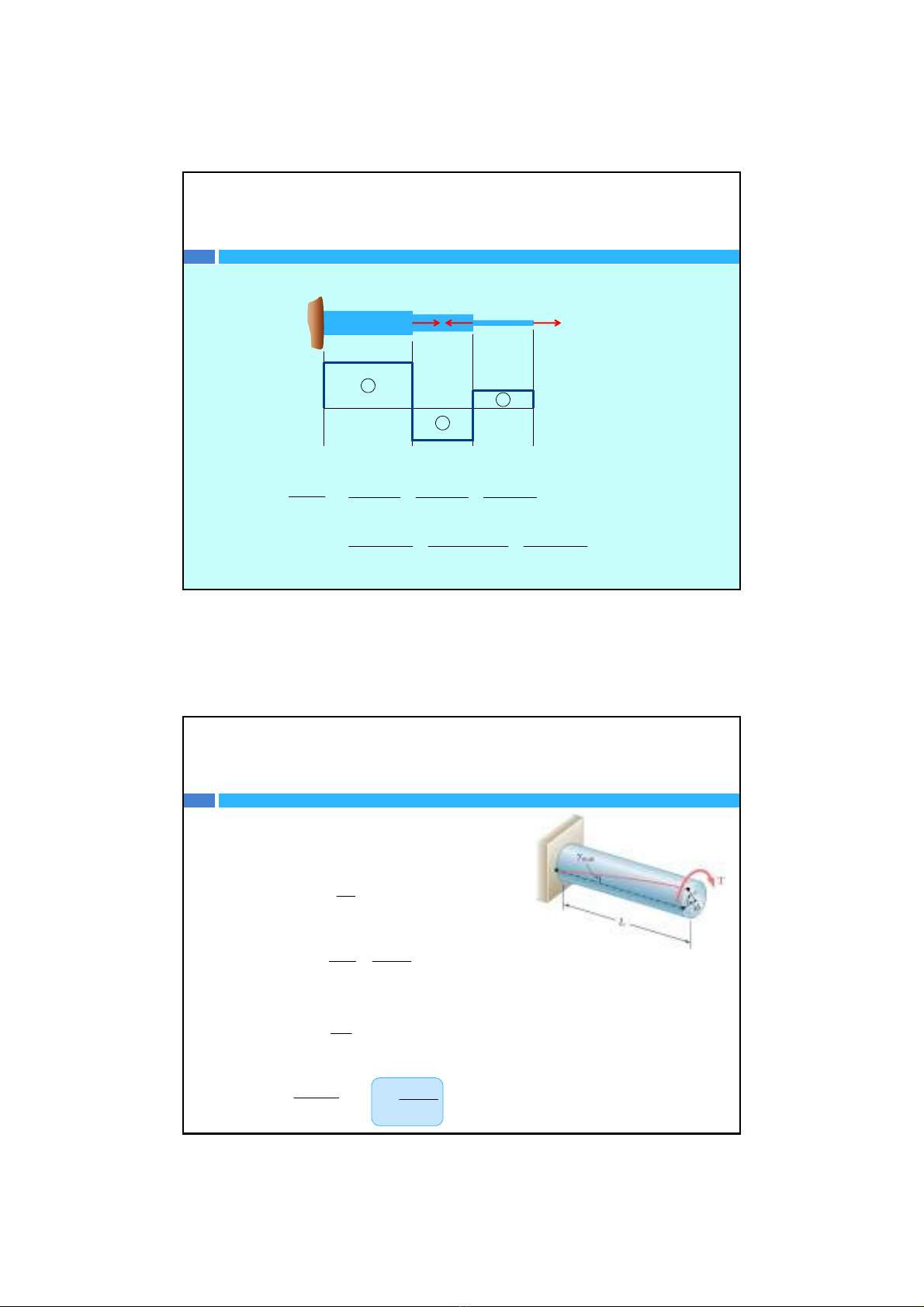
Trong trường hợpthanhkhôngđồng nhất(hệsốmô‐đun
đàn hồiEthayđổi, tiếtdiện thanh thay đổiA,nộilựcdọc
trụcN
zthay đổi), ta chia thanh này thành nhiềuđoạnsao
cho các hệsốtrên là hằng số.
Biếndạng dài tuyệtđốicủa thanh
1
n
zi i
iii
NL
EA

CHƯƠNG 6 Tính biếndạng của thanh
1. Thanh chịukéonénđúng tâm
Ví dụ:Cho thanh chịu kéo nén đúng tâm vớidiện tích mặtcắt
ngang và chịulực thay đổinhưhình vẽ.BiếtE=2.10
5N/mm2và
diện tích mặtcắt ngang là: AAB=20mm2;A
BC=30mm2;
ACD=60mm2.Tínhbiếndạng tuyệtđốicủa thanh.
D
CBA
2kN
5kN7kN
30mm 20mm 20mm
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 12
12/14/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 6 Tính biếndạng của thanh
1. Thanh chịukéonénđúng tâm
Vẽbiểuđồ nộilựcN
z
D
CBA
2kN
5kN7kN
2
2
33
44
+
+
‐
Biếndạng dài tuyệtđốicủa thanh
1
n
zi i
iii
NL
EA
B
CBC CDCD
AB AB
AB BC CD
NL NL
NL
EA EA EA

555
2000 20 ( 3000) 20 4000 30
2 10 20 2 10 30 2 10 60


   0, 01 (mm)

CHƯƠNG 6 Tính biếndạng của thanh
2. Thanh chịuxoắnthuầntúy
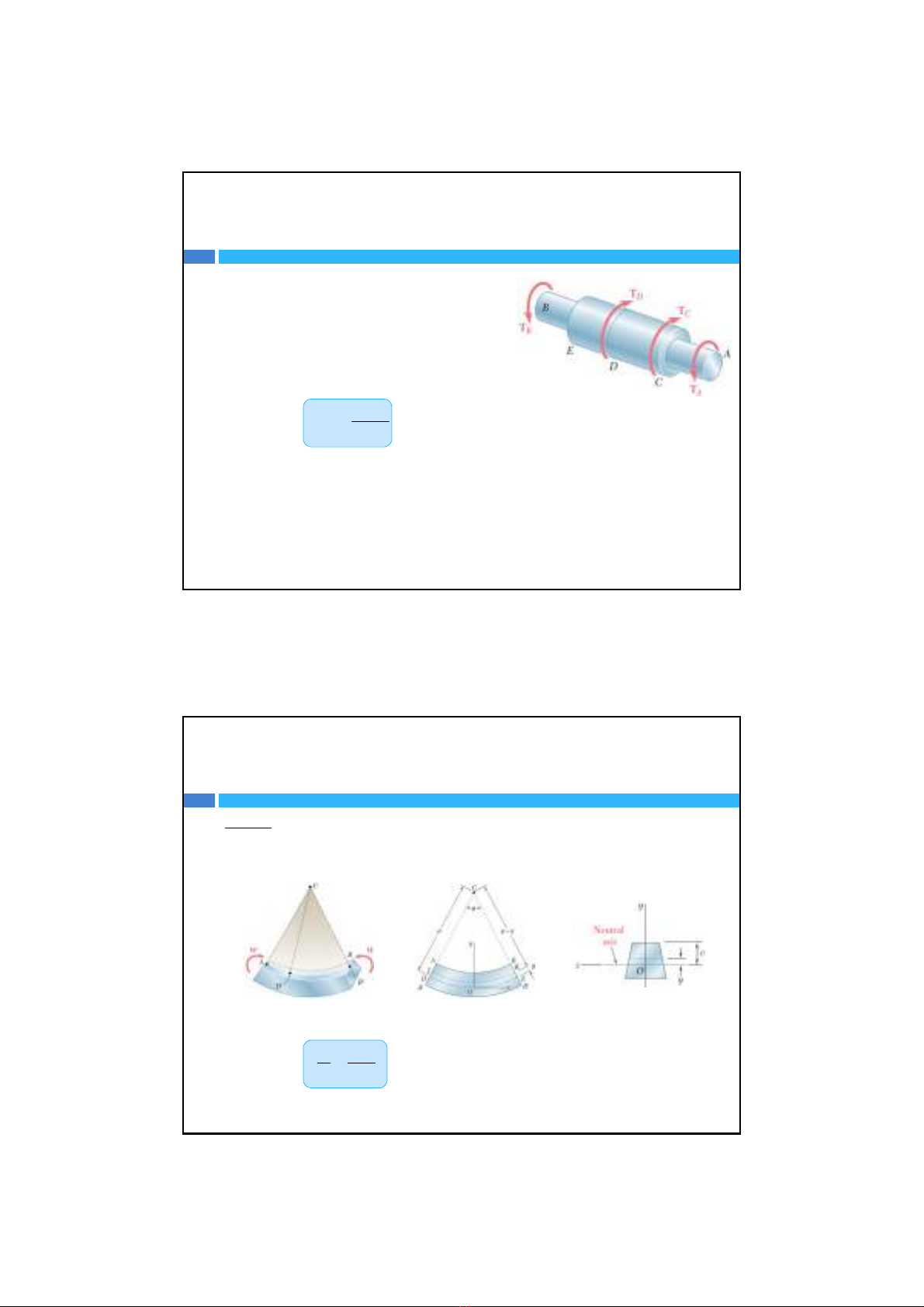
Xét trụcđồng nhấtchiều dài L và bán kính R
chịumô‐men xoắnT
Ứng suấttiếplớnnhất trong thanh
max
O
T
R
J
Theo định luật Hooke, ta được
max
max
O
TR
GGJ

Theo định nghĩabiếndạng góc tương đối
max
R
L
max
L
R
Góc xoắntuyệtđốicủatrục
O
TL
GJ

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 12
12/14/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 6 Tính biếndạng của thanh
2. Thanh chịuxoắnthuầntúy
Trong trường hợptrụckhôngđồng nhất(hệ
sốmô‐đun đàn hồitrượtGthayđổi, bán kính
Rthayđổi, mô‐men xoắnTthayđổi), ta chia
thanh này thành nhiềuđoạn sao cho các hệ
sốtrên là hằng số.
Góc xoắntuyệtđốicủa thanh
1
n
ii
iiOi
TL
GJ

CHƯƠNG 6 Tính biếndạng của thanh
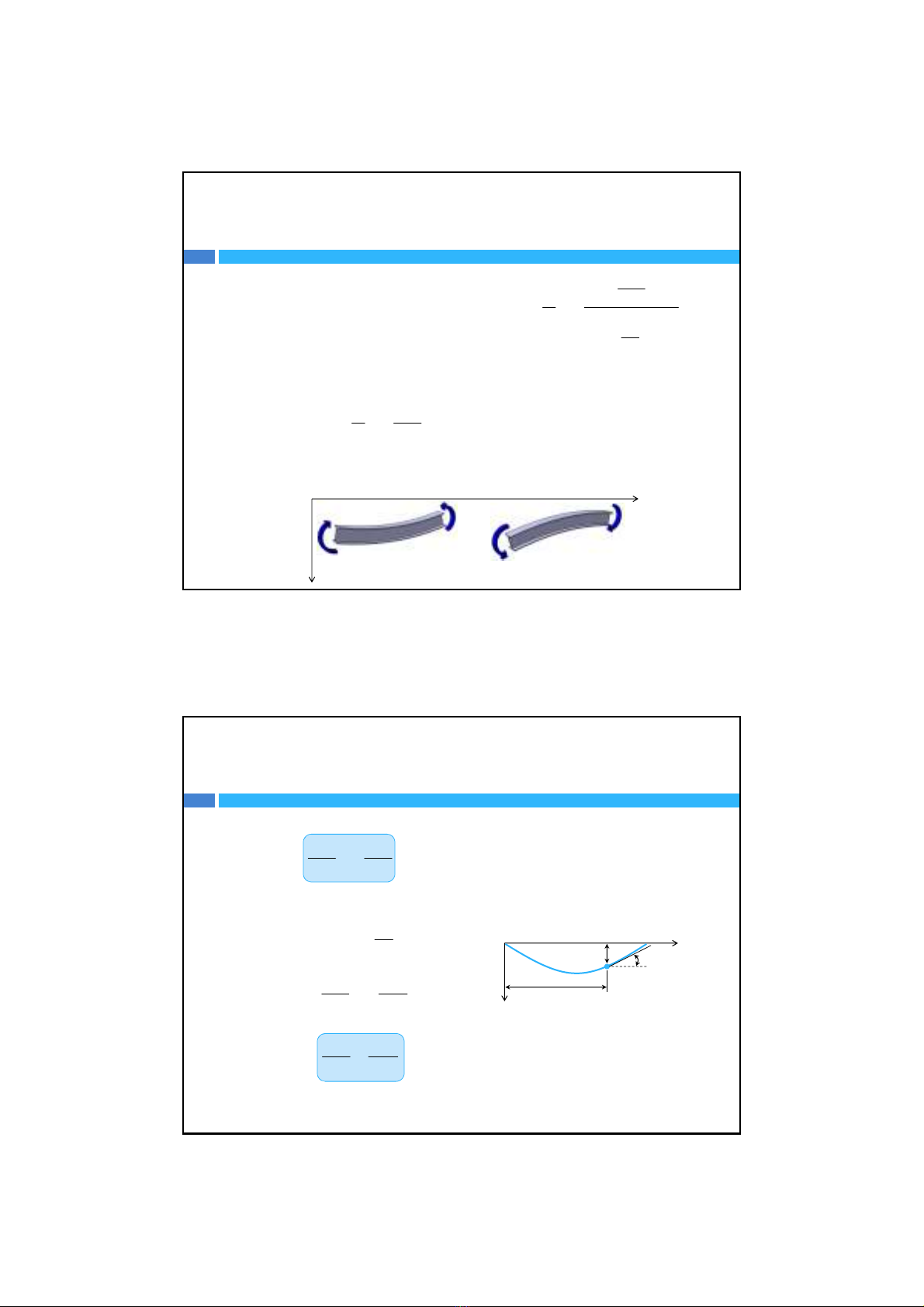
3. Thanh chịuuốn ngang phẳng
Xét một thanh dầmABchịumô‐men uốndương nhưhình vẽbên. Thanh
dầmsẽuốn quanh mộtđiểmCvới bán kính cong .
Bánkínhcongđượctínhbằng công thức
1
x
x
M
EJ
Cách 1: Sửdụng phương pháp giảitích(phương trình đường đàn hồi)
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 12
12/14/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 6 Tính biếndạng của thanh
3. Thanh chịuuốn ngang phẳng
Trong trường hợpdầmđàn hồinênđộ dốcdy/dzrấtbévìthếta có thểbỏ
đi các vô cùng bé bậccao
2
2
1dy
dz

Ta để biếtrằng dấucủad
2y/dz2và Mxluôn ngượcdấu. Nên ta thế1/vào
phương trình trên ta được
0; " 0
x
My
0; " 0
x
My
y
z
Mà theo công thứctoánhọc,bánkínhcong
củaquỹđạođượctínhbằng công thức
2
2
3/2
2
1
1
dy
dz
dy
dz




CHƯƠNG 6 Tính biếndạng của thanh
3. Thanh chịuuốn ngang phẳng
2
2
x
ddy
dz dz

Mối quan hệgiữa góc xoay và chuyểnvị
y
z
Q
()yz
z
()z
()
x
dy
zdz

x
x
x
dM
dz EJ

2
2
x
x
M
dy
dz EJ

Nên ta thế1/vào phương trình trên ta được