Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 13
12/14/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 7 Tính hệsiêu tĩnh
NỘIDUNG
2. Thanh chịuuốn ngang phẳng
1. Thanh chịukéonénđúng tâm
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
0
y
F
12
RPP
Nên dễdàng ta tính đượcphảnlực liên kếttạiđầuB
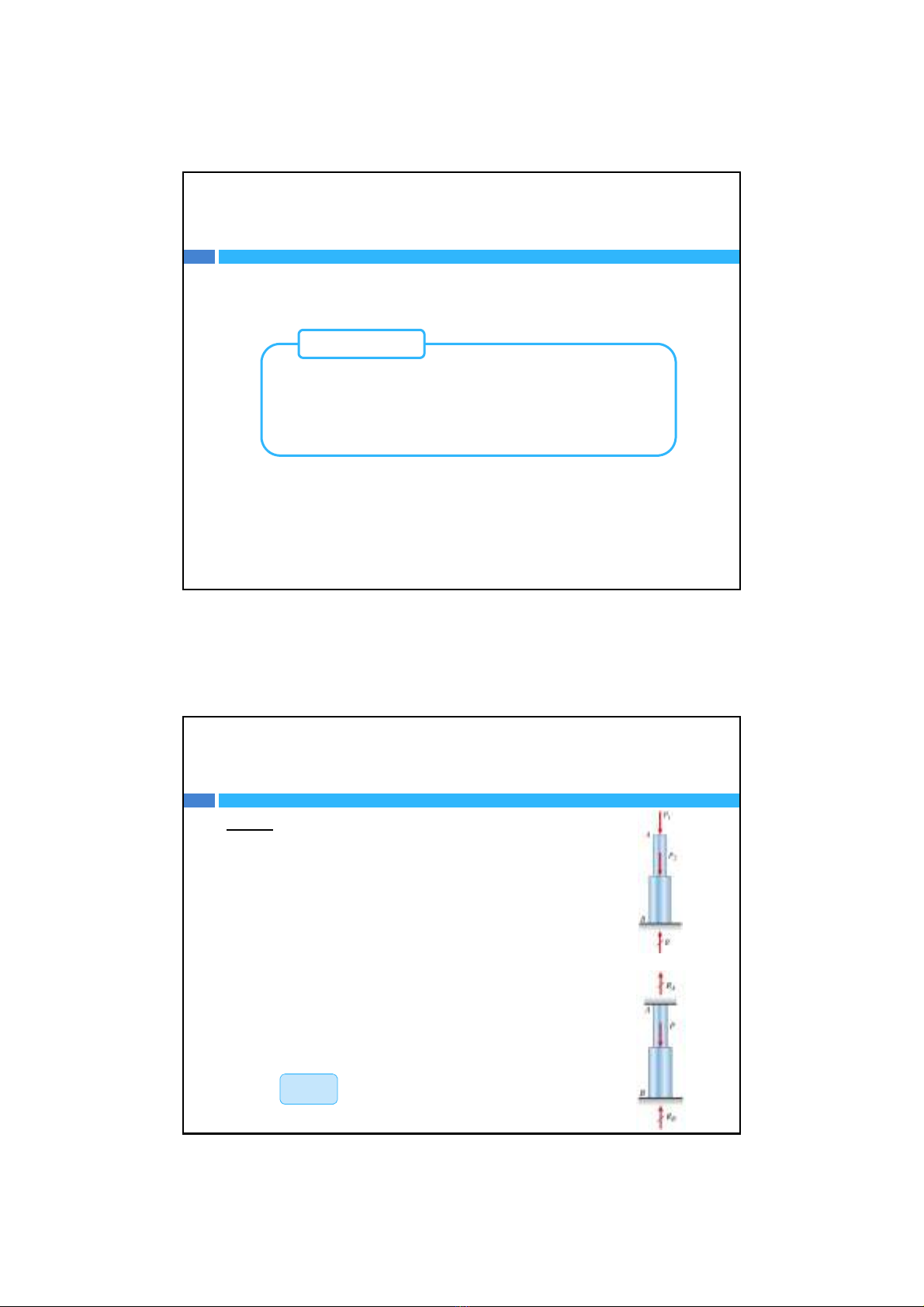
Xét thanh AB chịulựckéonénnhưhình vẽbên, ta nhận
thấyrằng bậctựdo củahệ0dof
Nhưng xét thanh AB chịulựckéonénnhưdưới, ta thấybậc
tựdo củahệ
0dof
Phương trình cân bằng lựcchohệ
0
y
F
AB
RPR
Hai phảnlực liên kếttạiAvàBlà2ẩnsốnên ta cầnthêm1
phương trình nữađể tìm 2 ẩnsốtrên
0
AB
Ta gọiđây là hệsiêu tĩnh
Ta gọiđây là phương trình tương thích
Tìm chuyểnvịtuyệtđốinhưbình thường theo 2 ẩnRA,RB
Cách 1: Dùng phương trình tương thích
Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 13
12/14/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
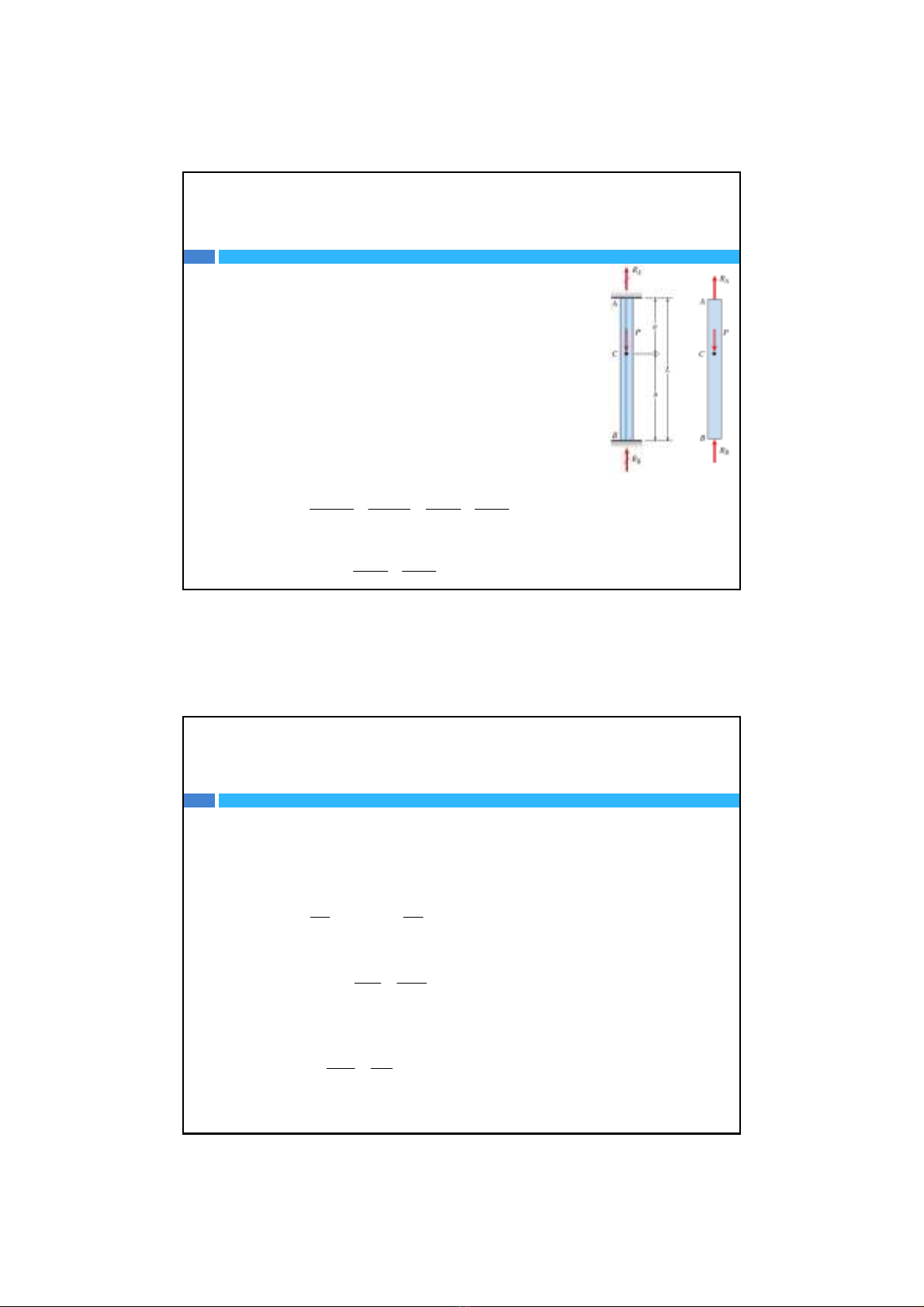
Xét thanh AB chiềudàiL,diệntíchtiếtdiệnlàAvàmô‐
đun đàn hồi E có liên kếtnhưhình vẽ. Tác dụng lựcPtại
điểmCcáchAđoạnanhưhình vẽ.
TạiđầuAvàBcó2phảnlực liên kếtnhưhình vẽ.
Theo công thức tính chuyểnvịtuyệtđốicủathanhchịu
kéo nén đúng tâm, ta được
AB AC CB


NộilựctrênđoạnACvàCBlà
AAC
N
R
AC CB
A
B
B
A
NaNb ab
EA EA EA EA
RR


Nên chuyểnvịtuyệtđốicủa thanh AB là
B
CB
N
R
Mà ta có phương trình tương thích
0
AB
0
AB
RR
ab
EA EA

 AB
bRaR
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
Dựavàophương trình cân bằng lựctađược
Dựavào2phương trình trên, dễdàng tính đượcphảnlực liên kếttạiA
và B là
AB
RPR
A
RPb
L
B
RPa
L
Từphảnlực liên kếtđãbiết, ta có thểtính chuyểnvịtạiđiểmC
A
CAC
Ra
P
ab
EA LEA


Tương tự,tacũng tính đượcứng suấttrongthanhtừthành phầnnộilực
đãbiết
AC
AC
NPb
AL

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 13
12/14/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
L
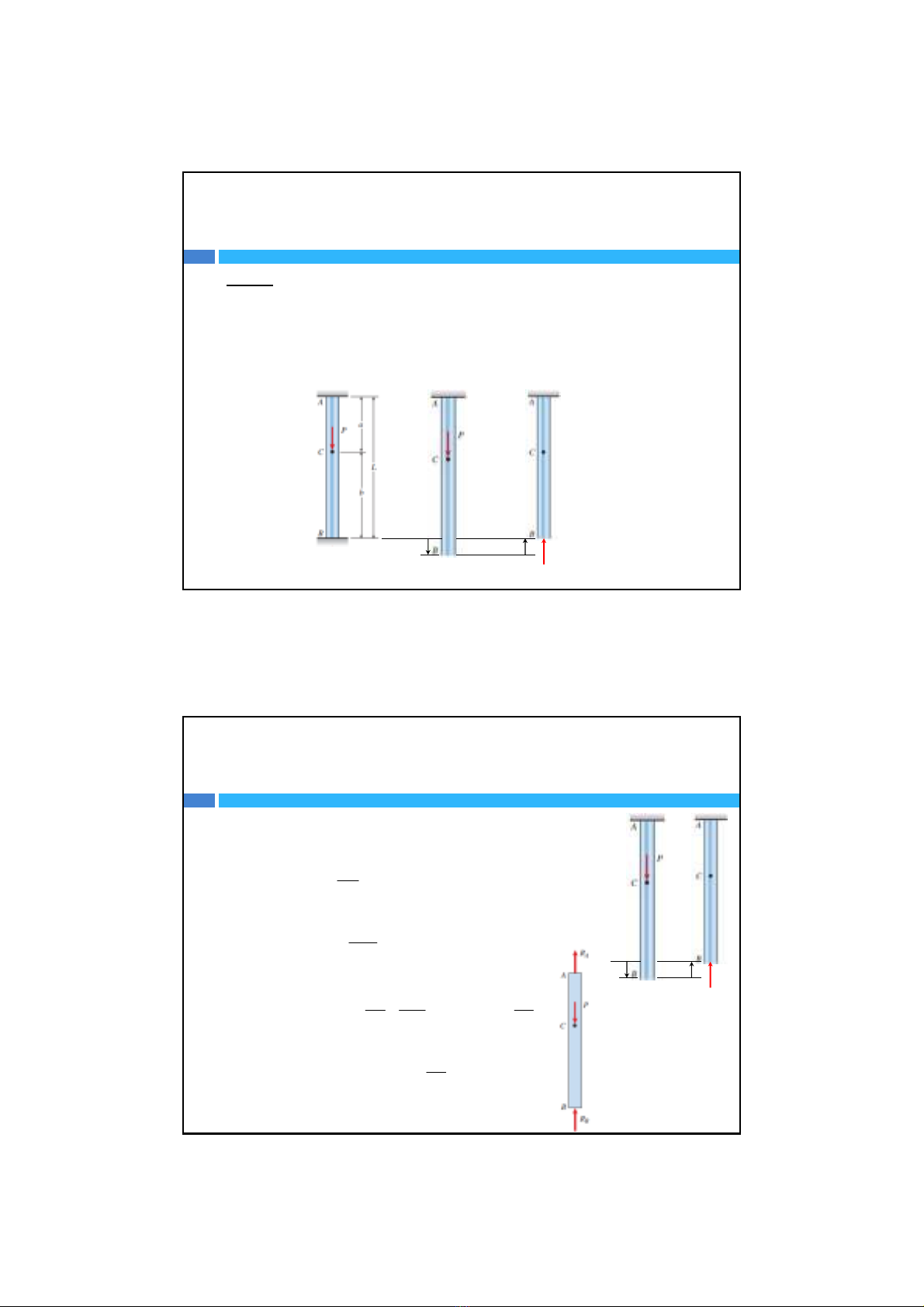
Cách 2: Dùng phương pháp cộng tác dụng
Để giải bài toán siêu tĩnh, ta có thểsửdụng phương pháp cộng tác dụng.
B
R
R
0
AB
Ta tách thành hai bài toán tính chuyểnvị:
1. Tính chuyểnvị
Ldo tảitrọng gây ra.
2. Tính chuyểnvị
Rchỉdo phảnlực liên kếtRBgây ra.
Vậy chuyểnvịtổng của thanh AB là AB L R

CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
Áp dụng phương pháp cộng tác dụng ta có
1. Tính chuyểnvị
Ldo tảitrọng gây ra.
L
P
a
EA
2. Tính chuyểnvị
Rchỉdo phảnlực liên kếtRBgây ra.
L
B
R
R
B
R
R
L
EA

Vậy chuyểnvịtổng của thanh AB là
0
AB L R

 0
B
RLPa
EA EA
 B
a
RP
L

Sửdụng phương trình cân bằng lựcđể tìm RA
0
B
ARPR A
b
RP
L

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 13
12/14/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
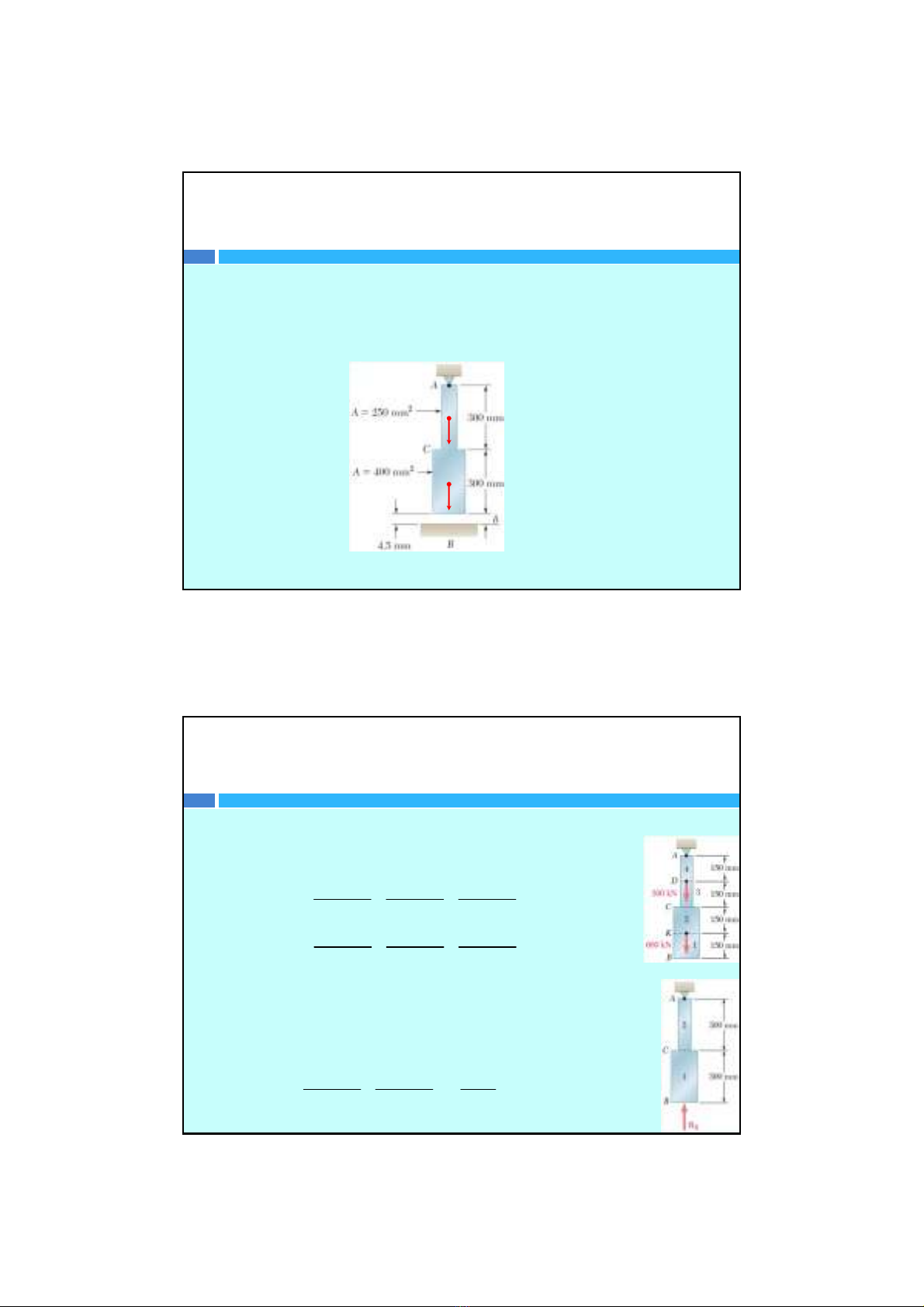
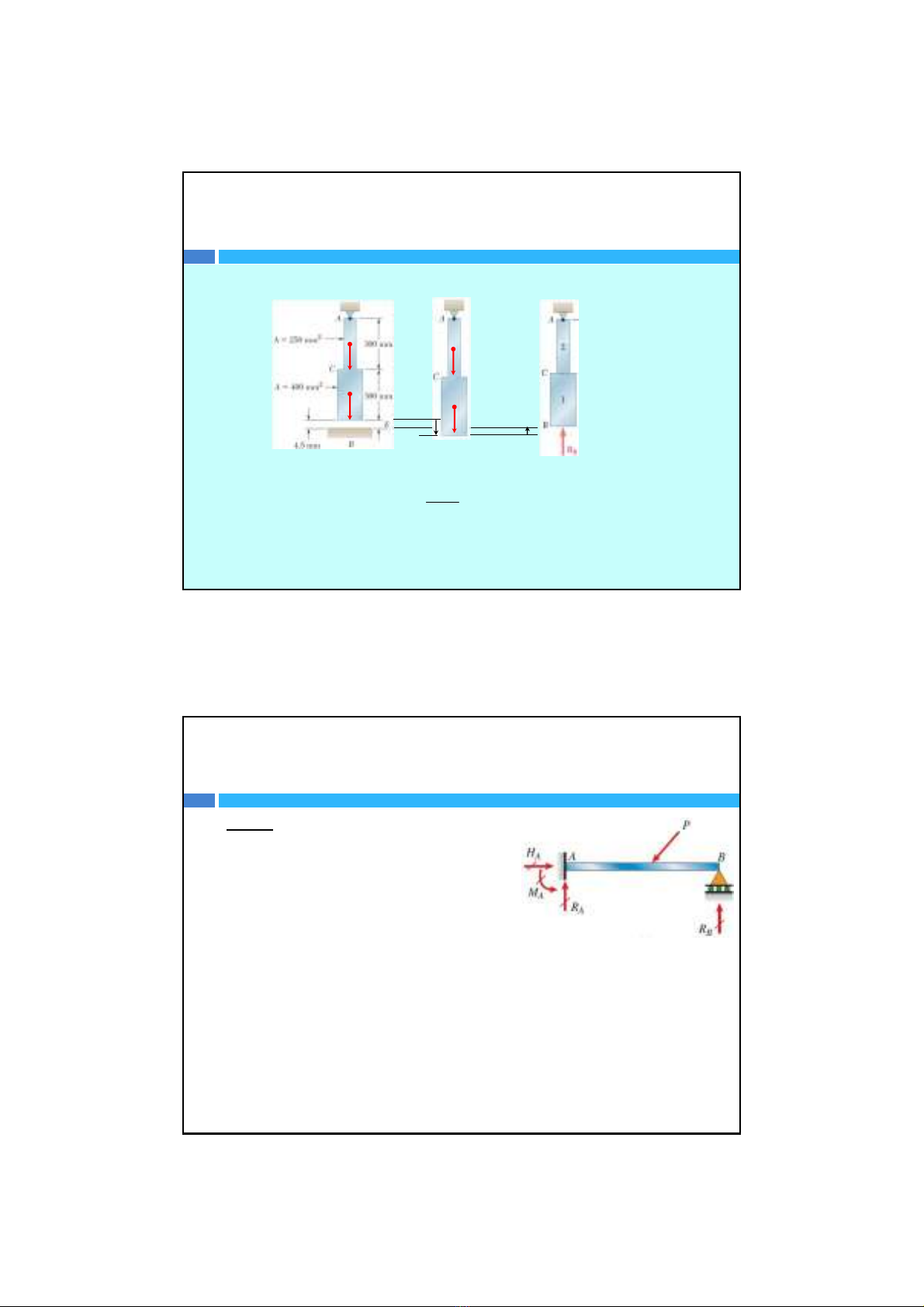
Ví dụ:Cho thanh chịu kéo nén đúng tâm vớidiện tích mặtcắt
ngang và chịulực thay đổinhưhình vẽ.Biết E=200 GPa. Tính
phảnlực liên kếttạiAvàBbiếtkhoảng cách đầu B cách mặt
nềnlà4,5mm
300 kN
600 kN
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
Trước tiên, ta phải tính chuyểnvịdo ngoạilựcgâyracólàmđầuB
chạm vào mặtnềnhaykhông
1. Tính chuyểnvị
Ldo tảitrọng gây ra.
600 150 600 150 900 150
0400 200 250 200 250 200
L



600 150 600 150 900 150
0 5,625 mm
400 200 250 200 250 200
L



Ta thấy chuyểnvịtuyệtđốicủa thanh AB khi chịungoạilực
5,625 mm 4,5 mm
L

Nên đầuBsẽchạmmặtnềntạiB.Dođó, tạiBcóphảnlực liên kếtRB
2. Tính chuyểnvị
Rchỉdo phảnlực liên kếtRBgây ra.
300 300 39
400 200 250 200 4000
B
R
B
B
RR R

 

Khoa Khoa Học Ứng Dụng
Bài giảng Cơ Học Ứng Dụng - Tuần 13
12/14/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 7 Tính hệsiêu tĩnh
1. Thanh chịukéonénđúng tâm
Theo nguyên lý cộng tác dụng ta được
AB L R

 39
5,625 4,5
4000
B
R
 115, 4 kN
B
R

300 kN
600 kN
L
300 kN
600 kN
R
Chuyểnvịtuyệtđốicủa thanh AB đúng bằng khoảng cách khe hở
Phương trình cân bằng lựctheophương đứng
300 600 0
B
A
RR 784,6 kN
A
R
CHƯƠNG 7 Tính hệsiêu tĩnh
2. Thanh chịuuốn ngang phẳng
Cách 1: Dùng phương trình đường đàn hồi
Xét thanh dầmABchịutảiPởgiữadầm,
ngàm tạiđầuAvàđầu B là liên kếtkhớpbản
lềtrượt (liên kếtđơn).
Phân tích phảnlực liên kếttađược4phảnlực
liên kết(4ẩnsố).
Nếusửdụng 3 phương trình cân bằng ta không thểtính được4ẩnsố!!
Vì thếta phảitìmriêngmộtẩnbằng cách sửdụng phương trình đường
đàn hồicủadầm.
Viếtphương trình đường đàn hồigiống nhưchương tìm chuyểnvịcủa
dầmnhưng liên kếtvẫngiữnguyên và trong phương trình đường đàn
hồicó1ẩnsốlà phảnlực liên kếtcần tính.
Dựavàođiềukiện liên kếttasẽtính đượcphảnlực liên kếtđó.