§1. Chuỗi số - Tổng quan về chuỗi số
Định nghĩa: Cho dãy số {un}. Ta gọi tổng tất cả các
số hạng của dãy (TỔNG VÔ HẠN)
1n
n
u
là chuỗi số
Ta gọi: 1. un là số hạng tổng quát của chuỗi
2. Tổng riêng thứ n của chuỗi là tổng n – số
hạng đầu tiên : Sn=u1+u2+…+un
3. Tổng của chuỗi là giới hạn hữu hạn (nếu có)
n
n
S lim S
Khi đó, ta nói chuỗi hội tụ. Ngược lại, tức là hoặc
không tồn tại giới hạn hoặc giới hạn ra vô tận thì ta
nói chuỗi phân kỳ
Vậy khi chuỗi hội tụ, chuỗi có tổng
1
lim
nn
n
n
u S S
CuuDuongThanCong.com https://fb.com/tailieudientucntt

§1. Chuỗi số - Tổng quan về chuỗi số
Ví dụ: Tìm số hạng tổng quát của các chuỗi:
1 3 7 15 ...
2 4 8 16
21
2
n
nn
u
2 3 4
2 2 2 2 ...
1 1.2 1.2.3 1.2.3.4
2
!
n
n
un
Ví dụ: Tính số hạng un của các chuỗi
1
2
41
n
n
n
Tính u5?
5
5 2 7
4.5 1 19
u
1
(2 1)!!
( 1)!
n
n
n
Tính u6
6
(2.6 1)!! 11!! 1.3.5.7.9.11 99
(6 1)! 7! 1.2.3.4.5.6.7 48
u
CuuDuongThanCong.com https://fb.com/tailieudientucntt

§1. Chuỗi số - Tổng quan về chuỗi số
Ta bắt đầu từ việc tính tổng riêng thứ n của chuỗi
2
1 ... n
n
S q q q
,1
1,1
1
n
nq
qq
q
Rõ ràng khi q=1, Sn=n thì chuỗi là phân kỳ
Khi |q|<1:
1
lim 1
n
n
SSq
qn→0 khi n→∞ nên
Tức là chuỗi hội tụ và có tổng là S
Dãy {Sn} không có giới hạn → chuỗi phân kỳ Khi |q|>1:
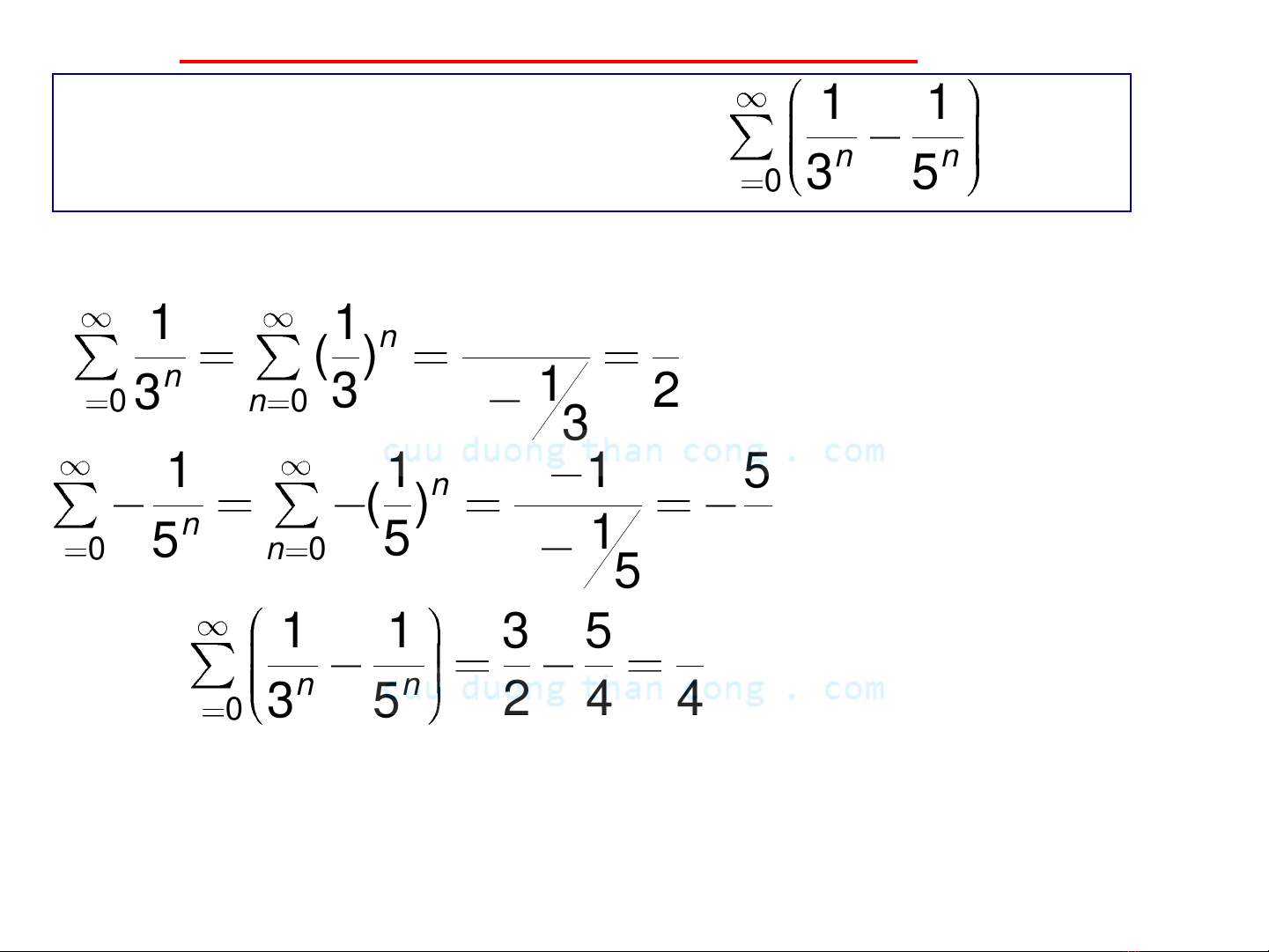
Ví dụ: Tính tổng của chuỗi cấp số nhân
0
n
n
q
Vậy chuỗi cấp số nhân
0
n
n
q
hội tụ khi và chỉ khi |q|<1
CuuDuongThanCong.com https://fb.com/tailieudientucntt