Chương 3
PHƯƠNG PHÁP TUYẾN TÍNH HÓA ĐIỀU HÒA
3.1. PHƯƠNG PHÁP TTHĐH
3.1.1. Khái quát chung
Ưu điểm:
-có thểáp dụng với các HT bậc thấp và bậ
c
cao;
-do nó sửdụng phương pháp phân tí
ch trên
miền tần sốcủa các HT tuyến tính nên rất dễ
dàng áp dụng và cho phép đánh giá các tham số
chuyển động trong HT;
- áp dụng tương đối dễdàng đối với các phần tử
phi tuyến cứng có trong các HTĐKTĐ.
Nhược điểm: là phương pháp tính toán gầ
n
đúng.
Việc nghiên cứu HTĐKTĐ phi tuyến bằ
ng
phương pháp tuyến tính hóa điều hòa được thự
c
hiện qua hai giai đoạn :
-giai đoạn 1: thay thếkhâu phi tuyế
n trong HT
bằng khâu tuyến tính tương đương, có HST phụ
thuộc vào các tham sốchuyển độ
ng trong HT;
bằng cách đó ta nhận được HST của HT đượ
c
tuyến tính hóa điều hòa;
-giai đoạn 2:bằng phương pháp bất kỳcủ
LTĐKTĐ tuyến tính, tìm chuyển động của HT đ
ã
tuyến tính hóa điều hòa.
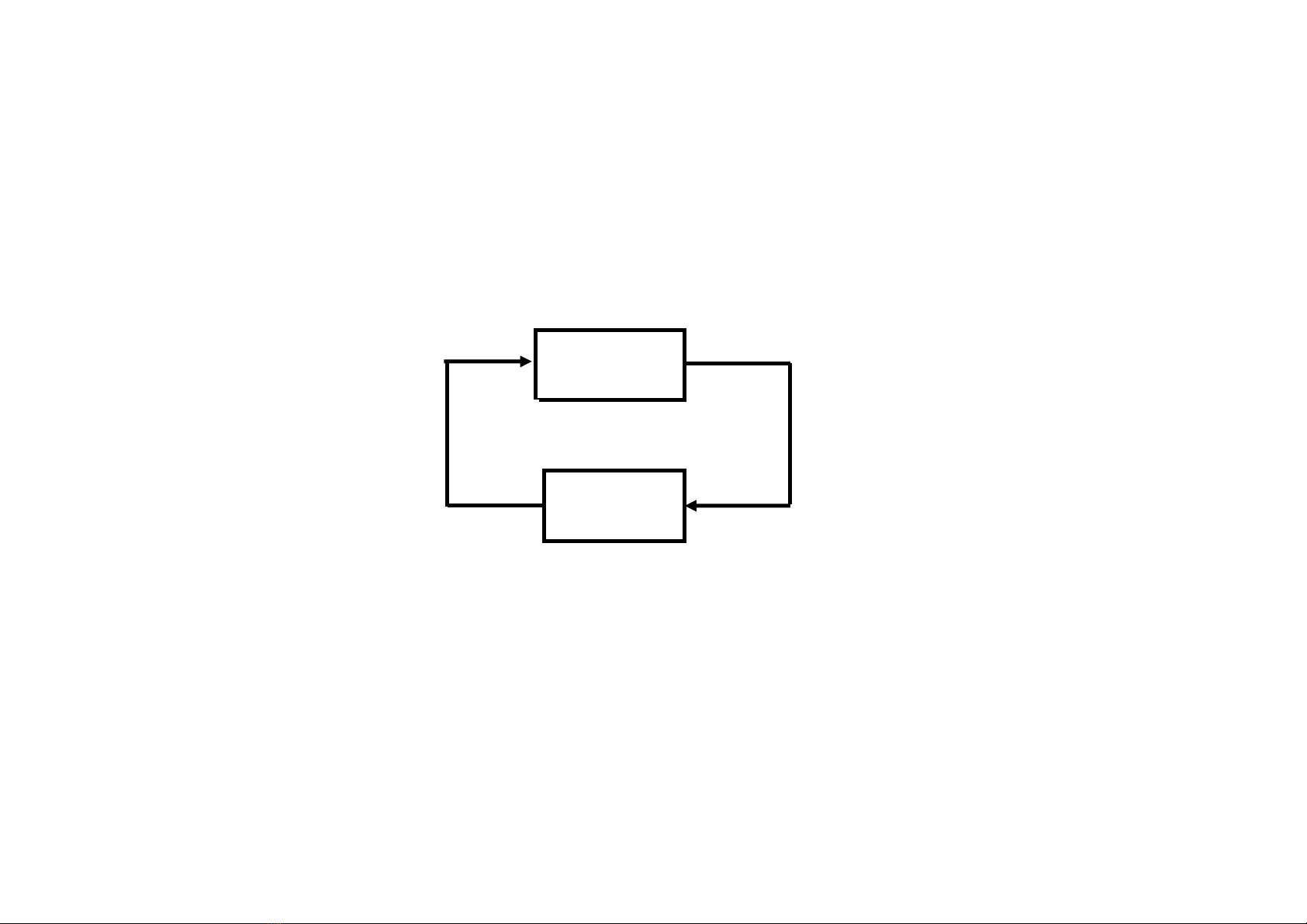
Để thực hiện phương pháp tuyến tính hóa điều
hòa thì trong cấu trúc của HT được nghiên cứu
cần tách ra phần tuyến tính và khâu phi tuyến
F(x) (H.3-1).
H. 3-1.
W
tt
(s)
F(x)
y(t) x(t)
Điều kiện áp dụng phương pháp tuyến tí
nh
hóa điều hòa:
- khâu phi tuyến tạo ra tín hiệu có hài bậc nhấ
t
trội hơn các hài bậc hai trởlên và không có
thành phần một chiều;
- phần tuyến tính có tính chất của bộlọc thấ
p
tần: loại bỏcác hài bậc cao.
Lúc này tín hiệu x(t) được làm gần đúng với hà
i
bậc nhất:
],)(sin[)()(
0
ψ
ψ
+
=
ttAtx
(3.1)