Bài giảng Mật mã ứng dụng: Giao thức trao đổi khoá - Đại học Bách khoa Hà Nội

Tài liệu này giới thiệu về các giao thức trao đổi khóa trong mật mã ứng dụng, một lĩnh vực quan trọng để thiết lập kênh liên lạc an toàn.

Sinh viên, nghiên cứu sinh và các chuyên gia trong lĩnh vực mật mã, an toàn thông tin và khoa học máy tính, những người quan tâm đến nguyên lý và ứng dụng của các giao thức trao đổi khóa.

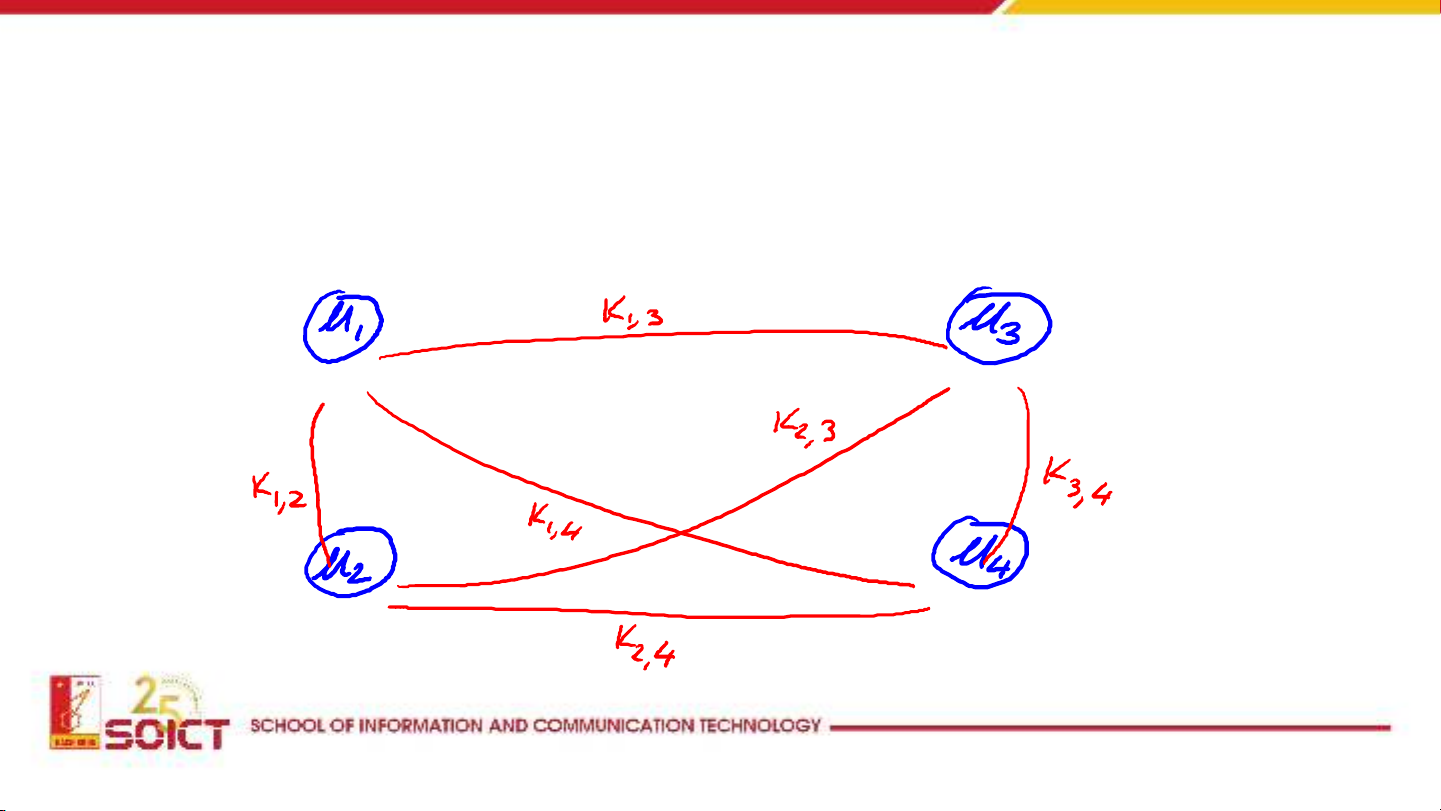
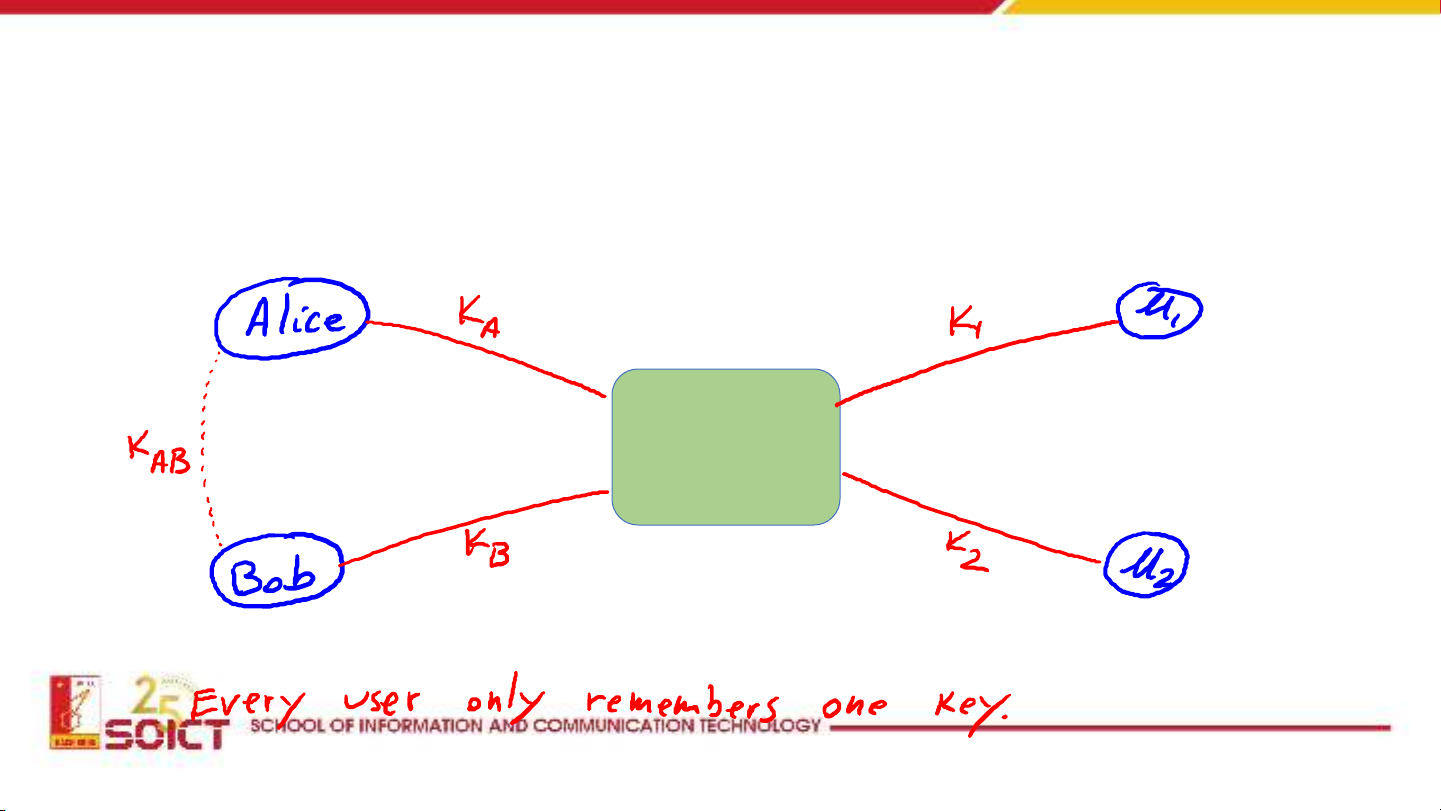
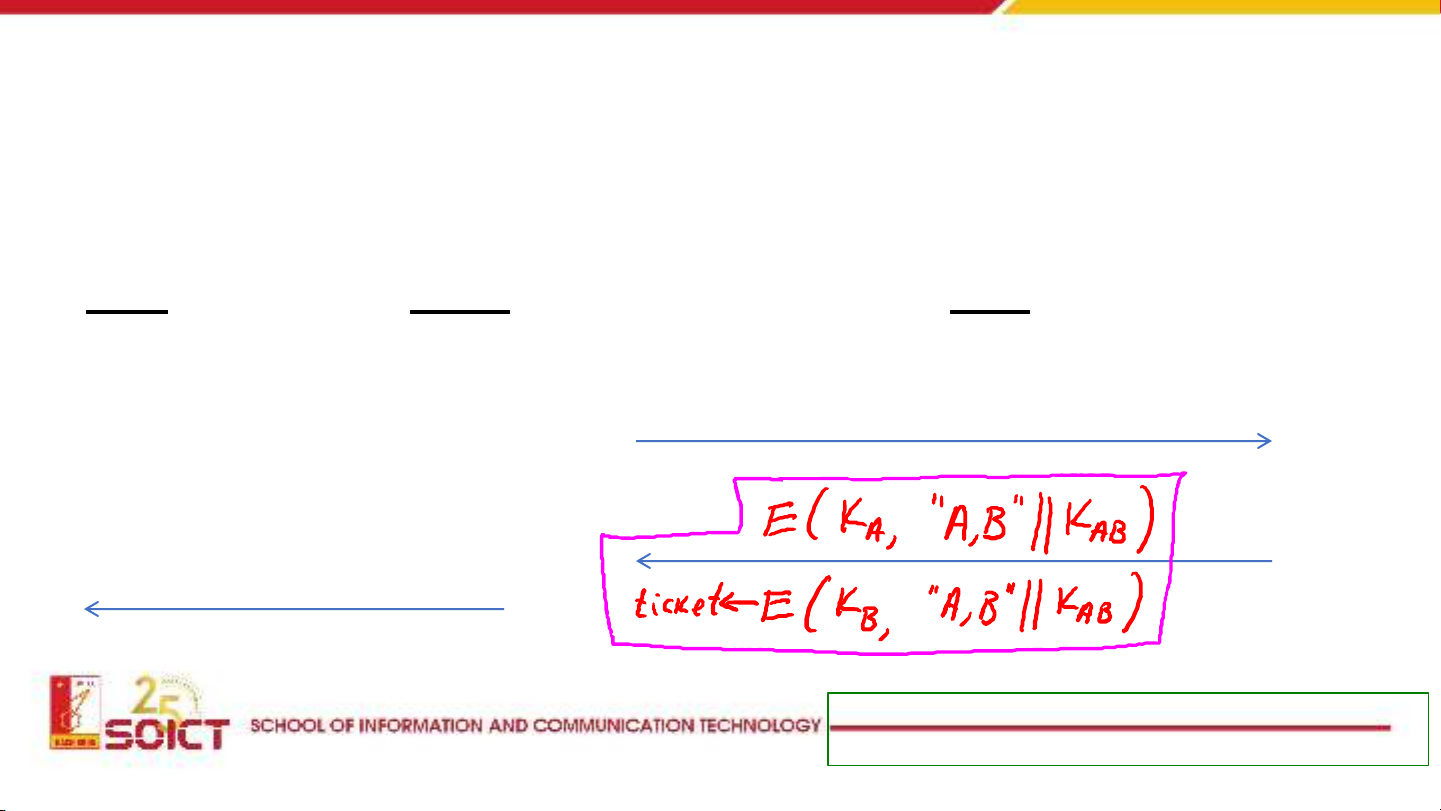
Tài liệu này trình bày chi tiết các giao thức trao đổi khóa trong lĩnh vực mật mã ứng dụng, bắt đầu từ các phương pháp truyền thống có sự tham gia của bên thứ ba tin cậy (TTP) và những hạn chế của chúng, đặc biệt là về khả năng chống lại các cuộc tấn công phát lại. Sau đó, tài liệu chuyển sang khám phá các giải pháp trao đổi khóa mà không cần bên thứ ba trực tuyến, đánh dấu sự ra đời của mật mã khóa công khai. Các giao thức cụ thể được phân tích bao gồm Merkle Puzzles (1974), làm rõ cơ chế hoạt động, hiệu quả và khả năng chống lại kẻ nghe trộm. Tiếp theo là giao thức Diffie-Hellman (1976), một cột mốc quan trọng trong việc thiết lập khóa bí mật qua kênh không an toàn, cùng với phân tích về tính an toàn dựa trên bài toán logarit rời rạc và lỗ hổng trước tấn công Man-in-the-Middle. Cuối cùng, tài liệu giới thiệu Hệ mật mã ElGamal (1984), giải thích cách nó chuyển đổi từ ý tưởng trao đổi khóa sang một hệ mã hóa khóa công khai hoàn chỉnh, bao gồm các thành phần, quy trình mã hóa/giải mã và hiệu năng.