1
CHƯƠNG 5: MÁY TURING (TURING MACHINE)
1. Mô tả máy Turing.
2. Ngôn ngữ chấp nhận bởi
TM
3. TM thực hiện hàm tính
4. Chương trình con.
1
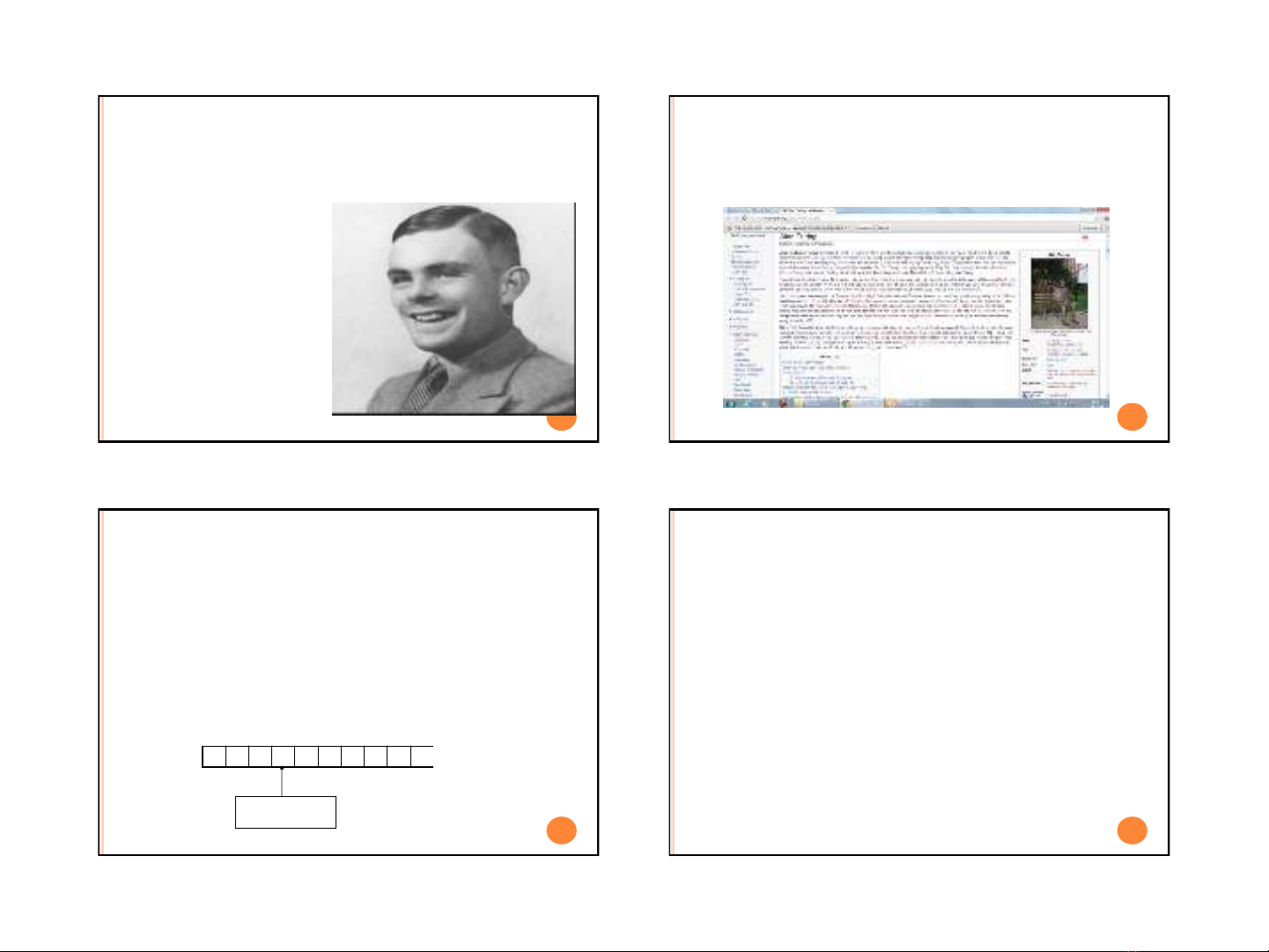
MÁY TURING ĐƯỢC GIỚI THIỆU BỞI
ALAN TURING VÀO NĂM 1936.
2
Tham khảo: http://vi.wikipedia.org/wiki/Alan_Turing
MÔ TẢ MÁY TURING.
Một máy Turing gồm:
Một bộ điều khiển hữu hạn.
Một băng được chia thành các ô để lưu dữ liệu.
Một đầu đọc – viết, mỗi lần đọc có thể duyệt qua một ô trên băng để
đọc hay viết ký hiệu.
a1 a2 … ai an B B B B …
3
Bộ điều khiển
Input, Bộ nhớ, Output
MÔ TẢ MÁY TURING (TT)
Mỗi bước chuyển của máy Turing, phụ thuộc vào ký hiệu
do đầu đọc đọc được trên băng và trạng thái của bộ điều
khiển, máy sẽ thực hiện các bước sau:
Chuyển trạng thái.
In một ký hiệu trên băng tại ô đang duyệt (nghĩa là thay
ký hiệu đọc được trên băng bằng ký hiệu nào đó).
Dịch chuyển đầu đọc – viết (sang trái (L), sang phải (R)
hoặc đứng yên ()).
Một cách hinh thức, ta định nghĩa máy Turing (TM) như
sau:
4
2
MÔ TẢ MÁY TURING (TT)
Định nghĩa: TM là một hệ thống gồm các thành phần M(, Q,
, , q0, B, F), trong đó:
: bộ ký hiệu nhập.
Q: tập hữu hạn các trạng thái.
: tập hữu hạn các ký tự được phép viết trên băng.
B: ký hiệu thuộc dùng để chỉ khoảng trắng trên băng (Blank).
: hàm chuyển ánh xạ: Q x Q x x {L, R, } ( có thể không
xác định với một vài đối với).
q0 Q là trạng thái bắt đầu.
F Q là tập các trạng thái kết thúc.
5
MÔ TẢ MÁY TURING (TT)
Một hinh thái (thể hiện) của máy Turing M được cho bởi 1q2, trong
đó q là trạng thái hiện hành của M; 12 * là nộ dung của băng tính
từ đầu băng cho tới ký hiệu khác Blank bên phải nhất của băng. Giả sử
Q và rời nhau: đầu đọc đang đọc ký hiệu bên trái nhất của 2 hoặc
nếu 2 = thì đầu đọc đọc Blank.
Hàm chuyển: Ta định nghĩa một phép chuyển trạng thái của TM như
sau:
Đặt X1X2…Xi-1qXi…Xnlà một thể hiện của TM.
Giả sử (q, Xi) = (p, Y, L), trong đó:
Nếu i – 1 = n thì Xi là B.
Nếu i= 1 thì không có ID kế tiếp, nghĩa là đầu đọc không được
phép vượt qua cận trái của băng.
6
MÔ TẢ MÁY TURING (TT)
Nếu i>1 ta viết:
X1X2…Xi-1qXi…Xn |M X1X2…Xi-2pXi-1YXi+1…Xn
Tương tự (q, Xi) = (p, Y, R) thì ta viết:
X1X2…Xi-1qXi…Xn |M X1X2…Xi-1YpXi+1…Xn
Tương tự (q, Xi) = (p, Y,) thì ta viết:
X1X2…Xi-1qXi…Xn |M X1X2…Xi-1pYXi+1…Xn
Chú ý rằng nếu i-1 = n thì chuỗi Xi…Xn là rỗng và
vế phải dài hơn vế trái, nghĩa là TM M mở rộng
chuỗi ký hiệu trên băng.
7
NỘI DUNG
1. Mô tả máy Turing.
2. Ngôn ngữ chấp nhận
bởi TM
3. TM thực hiện hàm tính
4. Chương trình con.
8
3
NGÔN NGỮ CHẤP NHẬN BỞI TM
Ngôn ngữ được chấp nhận bởi TM: Ký hiệu L(M): tập hợp
các chuỗi trong * là nguyên nhân đưa TM M đi đến trạng
thái kết thúc khi đã thực hiện việc thay thế từ bến trái các ký
hiệu trên băng của M với trạng thái bắt đầu q0. Một cách hình
thức, ta định nghĩa tập hợp ngôn ngữ được chấp nhận bởi TM
M(, Q, , , q0, B, F) là tập:
L(M) = {w| w * và q0w |*M 1p2 với p F còn 12
*}
Ví dụ 6.1:
Thiết kế TM chấp nhận ngôn ngữ L = {0n1n | n 1 }
9
GIẢI THUẬT
B1: Input : w = 0n1n
Output : yes , w L
No, w L
B2 : ý tưởng chung:
Khởi đầu TM chứa 0n1n bên trái nhất trên
băng sau đó là vô hạn khoảng trống Blank.
TM lặp lại quá trình sau:
10
GIẢI THUẬT (TT)
TM thay 0 bên trái nhất bằng X rồi chuyển sang phải tới 1 trái nhất,
TM thay 1 này bằng Y rồi dịch chuyển về bên trái cho tới khi gặp X
phải nhất nó chuyển sang phải một ô (tới 0 trái nhất) rồi tiếp tục lập
một chu trình mới.
Nếu trong khi chuyển sang phải để tìm 1 mà TM gặp Blank thì TM
dừng lại và không chấp nhận input. Tương tự, khi TM đã thay hết 0
bằng X và kiểm tra còn 1 trên băng thì TM cúng dừng và không chấp
nhận input.
TM chấp nhận input nếu như cũng không còn ký hiệu 1 nào trên
băng nữa.
B3: Thiết kế:
Đặt TM: M(, Q, , , q0, B, F) với các thành phần:
={0, 1}; Q={q0, q1, q2, q3, q4}; ={0,1, X, Y, B} và F={q4}
11
Ta có thể hình dung mỗi trạng thái là một câu lệnh hoặc
một nhóm câu lệnh trong chương trình. Trạng thái q0 là
trạng thái khởi đầu và nó làm cho ký hiệu 0 bên trái nhất
thay bằng X. Trạng thái q1 được dùng để tiến sang phải
bỏ qua các số 0 và Y để tìm 1 bên trái nhất. Nếu M tìm
thấy 1 nó thay bằng 1 bằng Y rồi đi vào trạng thái q2.
Trạng thái q2 đưa M tiến sang trái cho tới X đầu tiên và
đi vào trạng thái q0, dịch chuyển sang phải để tới 0 bên
trái nhất và tiếp tục một chu trình mới. Khi M tiến sang
phải trong trạng thái q1, nếu B hoặc X được tiếp thấy
trước 1 thì input bị loại bỏ (không chấp nhận) vì có chứa
nhiều ký hiệu 0 hơn 1 hoặc input không có dạng 0*1*.
12
4
Trạng thái q0 còn có vai trò khác. Nếu trạng thái q2 tìm
thấy X bên phải nhất thì ngay sau đó là Y thì các con số
0 đã được xét hết, do đó ở trạng thái bắt đầu một chu
trình mới q0 không tìm thấy ký hiệu 0 nào để thay thành
X mà chỉ gặp Y thì M đi vào trạng thái q3 duyệt qua các
Y để kiểm tra có hay không có ký hiệu 1 còn lại. Nếu
theo ngay sau các Y là B, nghĩa là trên băng nhập không
còn ký hiệu bào cả thì M sẽ đi vào q4 (trạng thái kết
thúc) để chấp nhận input. Ngược lại input bị loại bỏ.
Hàm chuyển được cho bởi bảng sau:
13
Ký hiệu
Trạng thái 0 1 X Y B
q0 (q1, X, R) - - (q3, Y, R) -
q1 (q1, 0, R) (q2, Y, L) - (q1, Y, R) -
q2 (q2, 0, L) - (q0, X, R) (q2, Y, L) -
q3 (q3, Y, R) (q4, B, )
q4 - - - - -
14
B4 : Các phép chuyển hinh thái của TM M trên input 0011:
q00011 | Xq1011 | X0q111 | Xq20Y1 | q2X0Y1 | Xq00Y1
| XXq1Y1 | XXYq11 | XXq2YY | Xq2XYY | XXq0YY |
XXYq3Y | XXYYq3 | XXYYq4
Output: Yes
B5: Thiết kế thuật toán
B6: Cài đặt thuật toán
B7: Testing Demo
15
NỘI DUNG
1. Mô tả máy Turing.
2. Ngôn ngữ chấp nhận bởi
TM
3. TM thực hiện hàm tính
4. Chương trình con.
16
5
MÁY TURNG THỰC HIỆN HÀM TÍNH
Ngôn ngữ được chấp nhận bởi một máy Turing được gọi là
ngôn ngữ đệ qui liệt kê. Lớp ngôn ngữ này rất rộng nó chứa
ngôn ngữ phi ngữ cảnh và một số ngôn ngữ khác.
Máy Turing như một máy tính hàm số nguyên:
Máy Turing cũng có thể được xem như là một máy tính của các hàm
số nguyên (đi từ tập số nguyên đến tập số nguyên).
Mỗi số nguyên ta viết dưới dạng số trong hệ nhất phân (unary), tức
là với một số i 0 ta viết thành chuỗi 0i (gồm i chữ số 0).
Nếu hàm f có k đối số i1, i2, …, ik thì ta viết lần lượt các số nguyên
này trên băng của TM ngăn cách nhau bởi 1, nghĩa là input có dạng
0i110i2…0ik. Nếu TM dừng (chấp nhận hoặc không chấp nhận) với
băng 0m thì ta nó f(i1,i2,…,ik) = m
17
MÁY TURNG THỰC HIỆN HÀM TÍNH (TT)
Ví dụ 6.2: Thiết kế máy Turing tính toán phép trừ riêng
Ta định nghĩa phép trừ riêng như sau:
Input: 0m10n
Output: 0m\n
18
m – n nếu m n
0 nếu m<n
f(m,n) = m\n =
MÁY TURNG THỰC HIỆN HÀM TÍNH (TT)
M lặp lại việc thay thế lần lược từng số 0 ở đầu băng bằng B rồi tiến
sang phải, ra sau 1 tìm 0 và thay thế 0 này bằng 1. M lại chuyển sang
trái cho đến khi gặp B đầu tiên thì dừng lại, trở về trạng thái bắt đầu và
tiếp tục vòng lặp như trên. M dừng nếu:
i. Khi tìm 0 bên phải, M gặp B. Lúc này M đã thay n số 0 bên phải
0m10n thành 1 và n+1 số 0 bên trái thành B, trường hợp này xảy ra
khi trong chuỗi input có m>n. Do vậy M phải thay lại tất cả n +1
số 1 sau thành B, và sau đó dịch trái thay trả lại một B về thành 0,
cuối cùng trên băng còn lại kết quả phép trừ là m-n số 0.
19
MÁY TURNG THỰC HIỆN HÀM TÍNH (TT)
ii. Khi bắt đầu một vòng lặp mới, M không tìm thấy 0 để
đổi thành B, lúc này m số 0 đầu đã bị đổi thành B,
trường hợp này xảy ra khi m n. Khi đó, M thay tất cả
các sô1 1 và 0 trên băng thành B để cho kết quả phép
trừ thành 0 (biểu diễn gồm toàn ký hiệu B trong hệ
nhất phân).
Ta xây dựng TM như sau: M({0, 1}, {q0, q1,…, q6}, {0, 1,
B}, , q0, B, {q6}).
TM sẽ bắt đầu bằng 0m10n trên băng và kết thúc với 0m\n
trên băng. Các phép chuyển trạng thái được định nghĩa
như sau: 20