1
TRƯỜNG ĐẠI HỌC NÔNG LÂM TP. HỒ CHÍ MINH
KHOA MÔI TRƯỜNG & TÀI NGUYÊN | BỘ MÔN GIS & TÀI NGUYÊN
Phân tích hình mẫu không gian
(Spatial pattern analysis)

Copyright © 2024 | nguyenduyliem@hcmuaf.edu.vn Phân tích không gian I
Nội dung
Hình mẫu không gian là gì? (What is spatial pattern?)
Tại sao cần phân tích hình mẫu không gian (Why analyze spatial pattern?)
Chỉ số nhận diện hình mẫu không gian toàn cục (Global statistics to identify
spatial patterns)
Hình mẫu của các vị trí (The spatial pattern of feature locations)
Hình mẫu của các thuộc tính (The spatial pattern of feature values)
Chỉ số nhận diện phân cụm cục bộ (Local statistics to identify clusters)
Phân cụm của các vị trí (The clusters of features)
Phân cụm của các thuộc tính (The clusters of similar values)
2
Copyright © 2024 | nguyenduyliem@hcmuaf.edu.vn Phân tích không gian I
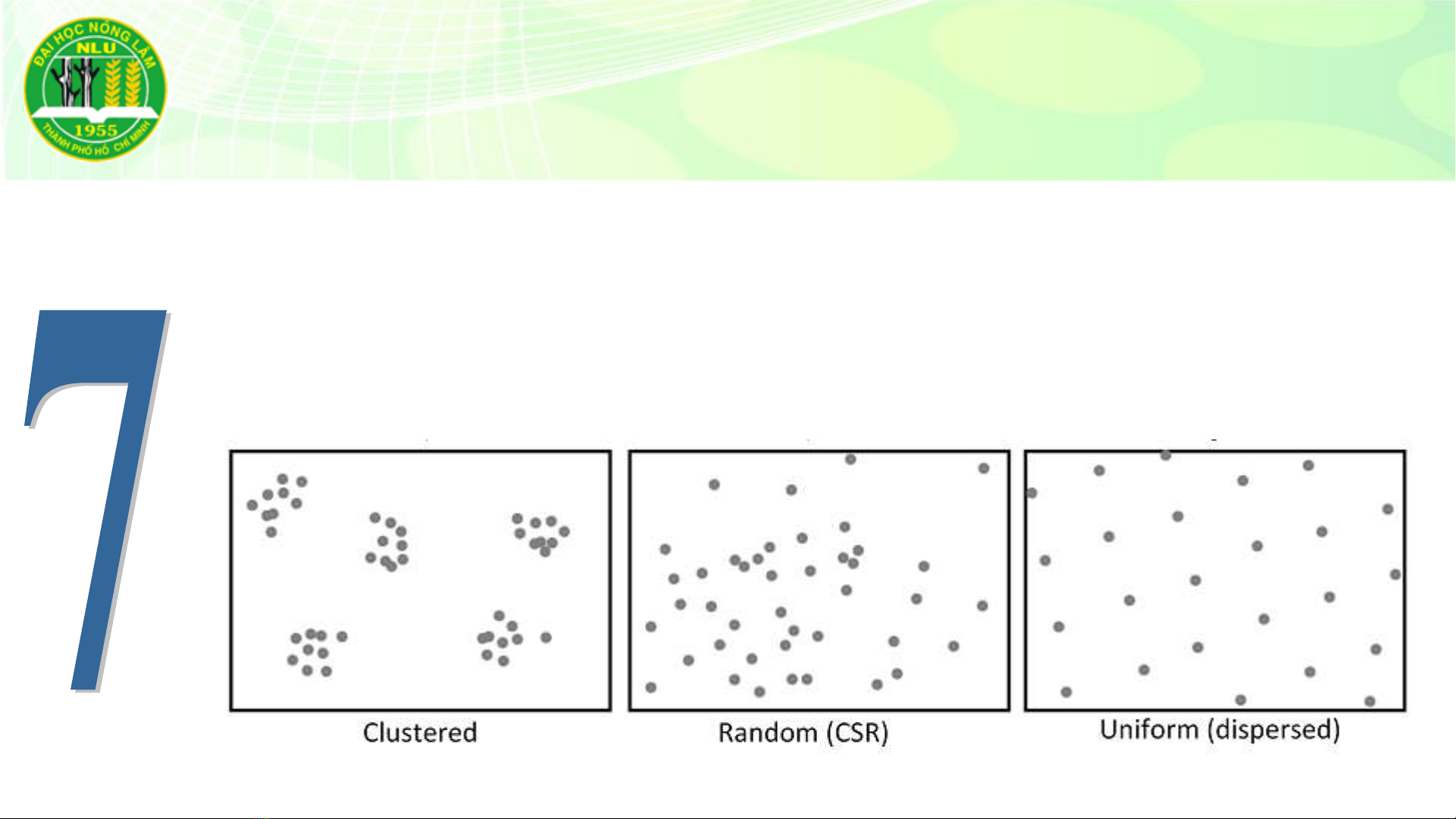
Hình mẫu không gian là gì?
Phân bố của các đối tượng theo vị trí
hoặc thuộc tính trong một khu vực xác
định sẽ tạo ra một hình mẫu không gian.
Phân tán (dispersed)
Ngẫu nhiên (random)
Phân cụm (clustered)
3
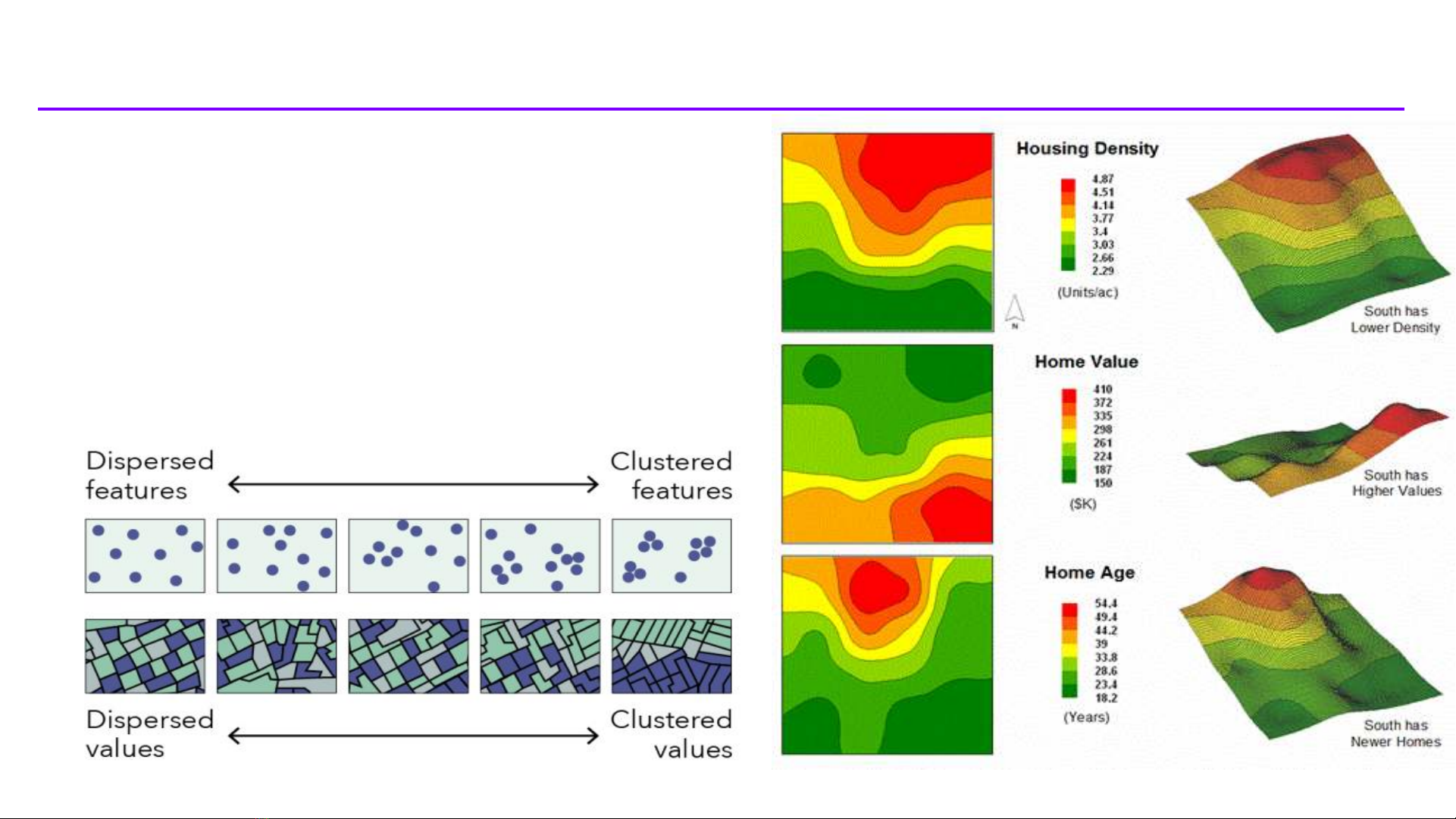
Hình mẫu không gian của mật độ (density),
giá bán (value), tuổi (age) của nhà ở
Random features
Random values

Copyright © 2024 | nguyenduyliem@hcmuaf.edu.vn Phân tích không gian I
Phân loại hình mẫu không gian
Phân tán
Các đối tượng cách nhau khoảng cách gần như không đổi.
Ví dụ: Trồng cây con trong vườn ươm với khoảng cách đều.
Ngẫu nhiên
Phân bố đối tượng hoàn toàn không thể đoán trước: Vùng
điểm dày đặc có thể nằm ngay cạnh vùng điểm thưa thớt.
Ví dụ: Giọt mưa rơi xuống mặt đất.
Phân cụm
Một số đối tượng nằm gần nhau hơn nhiều so với các đối
tượng khác, tạo ra các khoảng trống không gian.
Ví dụ: Trong rừng tự nhiên, cây con của một cây trưởng
thành nằm rất gần cây mẹ, nơi hạt giống được gieo xuống và
nảy mầm.
4

Copyright © 2024 | nguyenduyliem@hcmuaf.edu.vn Phân tích không gian I
Tại sao cần phân tích hình mẫu không gian?
Hiểu rõ bản chất về một hiện tượng địa lý
5
Nghiên cứu hành vi của động vật
hoang dã chỉ ra:
Các nhóm cá thể trong một khu vực bị
phân tán, nghĩa là loài đó có thể sống
trong nhiều sinh cảnh.
Các nhóm cá thể phân cụm, nghĩa là loài
đó cần các yêu cầu sinh cảnh cụ thể và
chỉ sống ở những nơi có điều kiện sinh
cảnh phù hợp.
Sinh cảnh của Le hôi miền Tây
phân tán khắp Wyoming (một
tiểu bang thuộc miền núi phía
Tây của miền Tây Hoa Kỳ)
Sinh cảnh của Le hôi cổ đỏ
phân cụm














![Quy hoạch tổng thể Cà Mau: Tài liệu [mới nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250827/tghong1621@gmail.com/135x160/49401756278390.jpg)


![Bài giảng Hàng hải địa văn [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250729/vijiraiya/135x160/43361753782101.jpg)
![Bài giảng Trắc địa cơ sở [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250729/vijiraiya/135x160/84_bai-giang-trac-dia-co-so.jpg)





![Atlas tài nguyên nước Việt Nam: Tài liệu [Mô tả/Hướng dẫn/Chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250715/vijiraiya/135x160/348_tai-lieu-atlas-tai-nguyen-nuoc-viet-nam.jpg)
![Hệ thống câu hỏi ôn tập Vùng kinh tế [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/kimphuong1001/135x160/76921752140578.jpg)
