

KhoaKhoa
KH & KTMTKH & KTMT
BK
TP.HCM
©2012, CE Department
KhoaKhoa
KH & KTMTKH & KTMT
BộBộmônmôn KỹKỹThuậtThuật MáyMáy TínhTính


Tài liu tham kho
• “Digital Systems, Principles and Applications”,
8th/5th Edition, R.J. Tocci, Prentice Hall
• “Digital Logic Design Principles”, N.
Balabanian & B. Carlson
–
John Wiley &
©2012, CE Department
Balabanian & B. Carlson
–
John Wiley &
Sons Inc., 2004
2


Đại Đại
sốsố
BK
TP.HCM
Đại Đại
sốsố
cáccác cổngcổng luậnluận lýlý
©2012, CE Department


Ni dung
•Đi sBoole
•Đi schuyn mch
• Các cng lun lý
©2012, CE Department 4


Đi s Boole
•Đi sBoole đưc thgii bitđn lnđu tiên bi
George Boole qua tác phm “An Investigation of the
Laws of Thought” vào năm 1854
• Các hng và bin Boole ch đưc mang 2 giá tr0
hoc1(LOW /HIGH )
–
Các
bin
Boole
biu
din
cho
mt
khong
đin
áp
trên
–
Các
bin
Boole
biu
din
cho
mt
khong
đin
áp
trên
đưng dây hoc ti ngõ nhp/ngõ xut ca mch
– Giá tr0hoc1đưc gi là mc lun lý (logic level)
©2012, CE Department 5
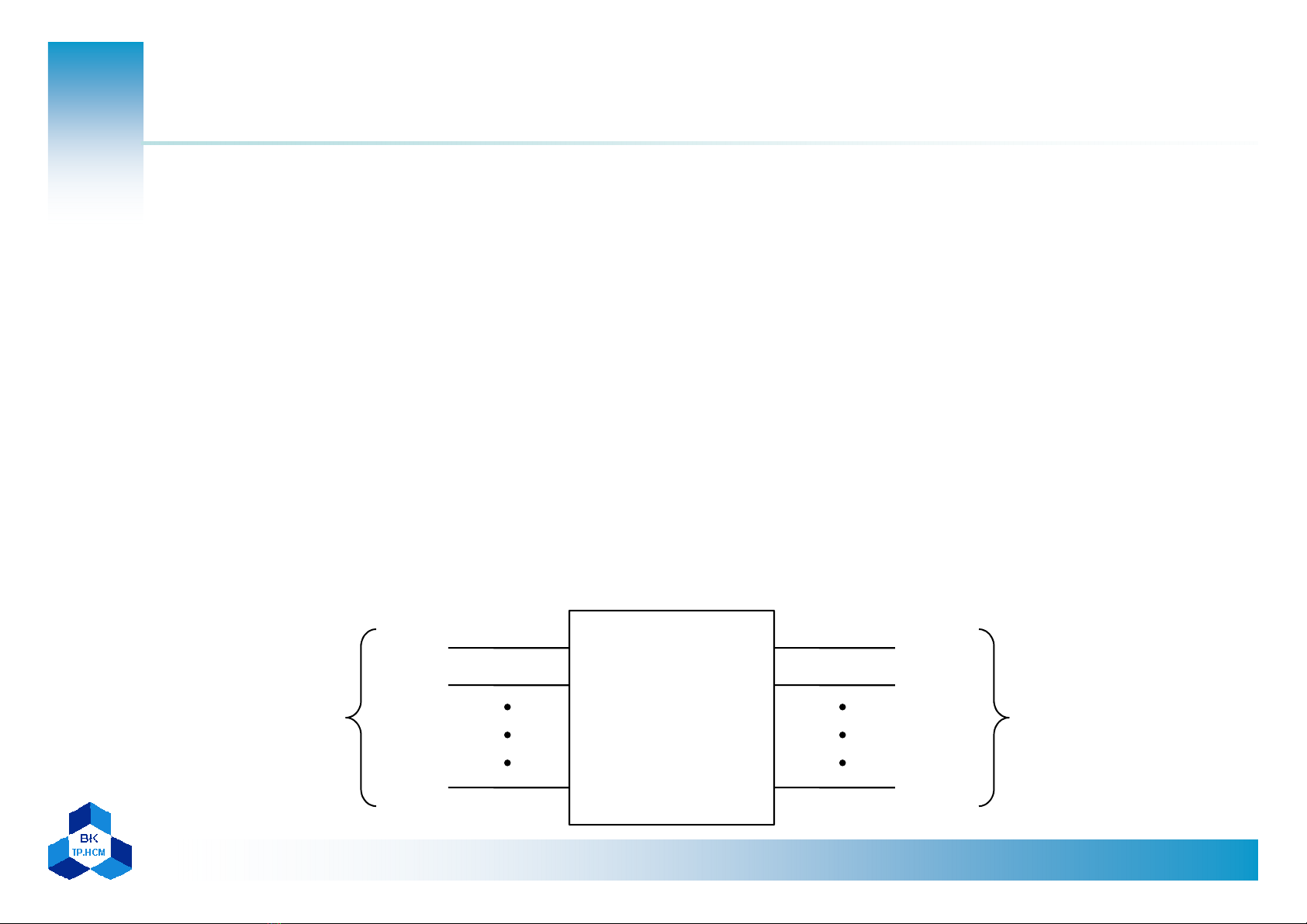
Mch
lun lý
ngõ nhp ngõ xut
A
x
F
y