
THỦY LỰC ĐẠI CƢƠNG
CHƢƠNG 7 – DÒNG CHẢY ĐỀU KHÔNG ÁP TRONG KÊNH
7.1. KHÁI NIỆM CHUNG
7.2. MẶT CẮT KÊNH
7.3. CÁC BÀI TOÁN VỀ KÊNH HÌNH THANG
7.4. TÍNH TOÁN KÊNH PHỨC TẠP
7.5. LƯU TỐC TÍNH TOÁN CHO PHÉP
7.1. KHÁI NIỆM CHUNG
7.1.1. Dòng chảy đều không áp trong
kênh
Dòng chảy không áp trong kênh là
dòng chảy có mặt hoáng tiếp xúc với
khí trời,
Dòng chảy ổn định là dòng chảy có lưu
lượng, diện tích mặt cắt ướt, đồ phân
bố lưu tốc trên mặt cắt ướt không thay
đổi dọc theo chiều dòng chảy.
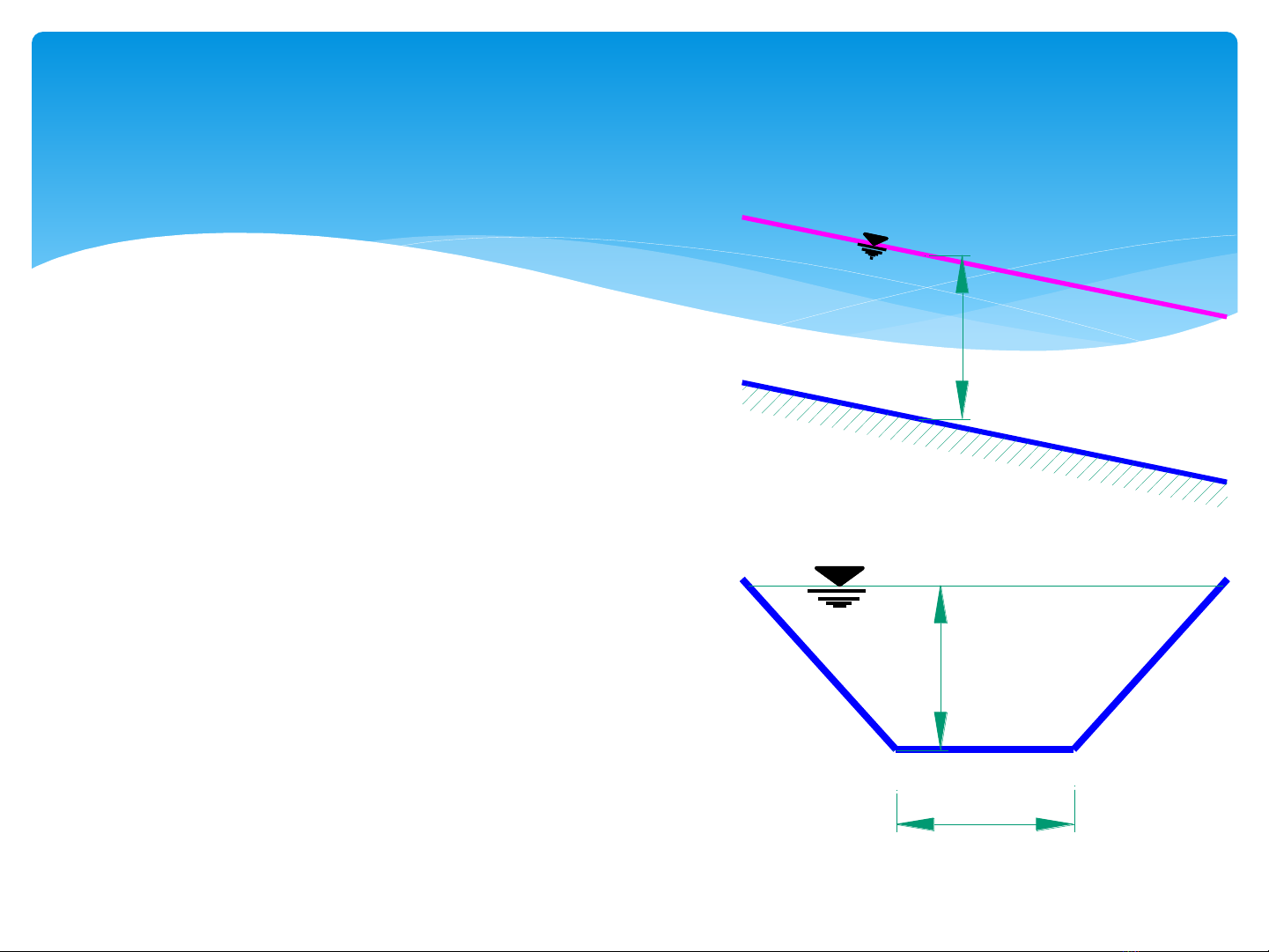
h0
J
i
h0
b
m

7.1. KHÁI NIỆM CHUNG
Các điều kiện để có dòng chảy ổn định đều không áp
1. Lưu lượng không đổi theo thời gian và dọc theo dòng chảy, Q(t,l)=Const.
2. Hình dạng mặt cắt, chu vi và diện tích mặt cắt ướt không đổi dọc theo
dòng chảy. Nên độ sâu mực nước trong kênh h(l)=const.
3. Độ dốc đáy không đổi, i=const.
4. Hệ số nhám cũng không đổi, n=const.
5. Phân bố lưu tốc trên các mặt cắt là không đổi dọc theo dòng chảy.
7.1. KHÁI NIỆM CHUNG
7.1.2 Công thức tính toán cơ bản
Dòng chảy đều trong kênh hở thường là
dòng chảy rối, ở khu sức cản bình
phương,
+ Công thức tính vận tốc:
v C RJ (m / s)=
+ Độ sâu dòng đều không đổi dọc theo dòng chảy, nên có: i = J
+ Công thức tính vận tốc trên được viết lại:
v C Ri
+ Công thức tính lưu lượng:
Q v C Ri
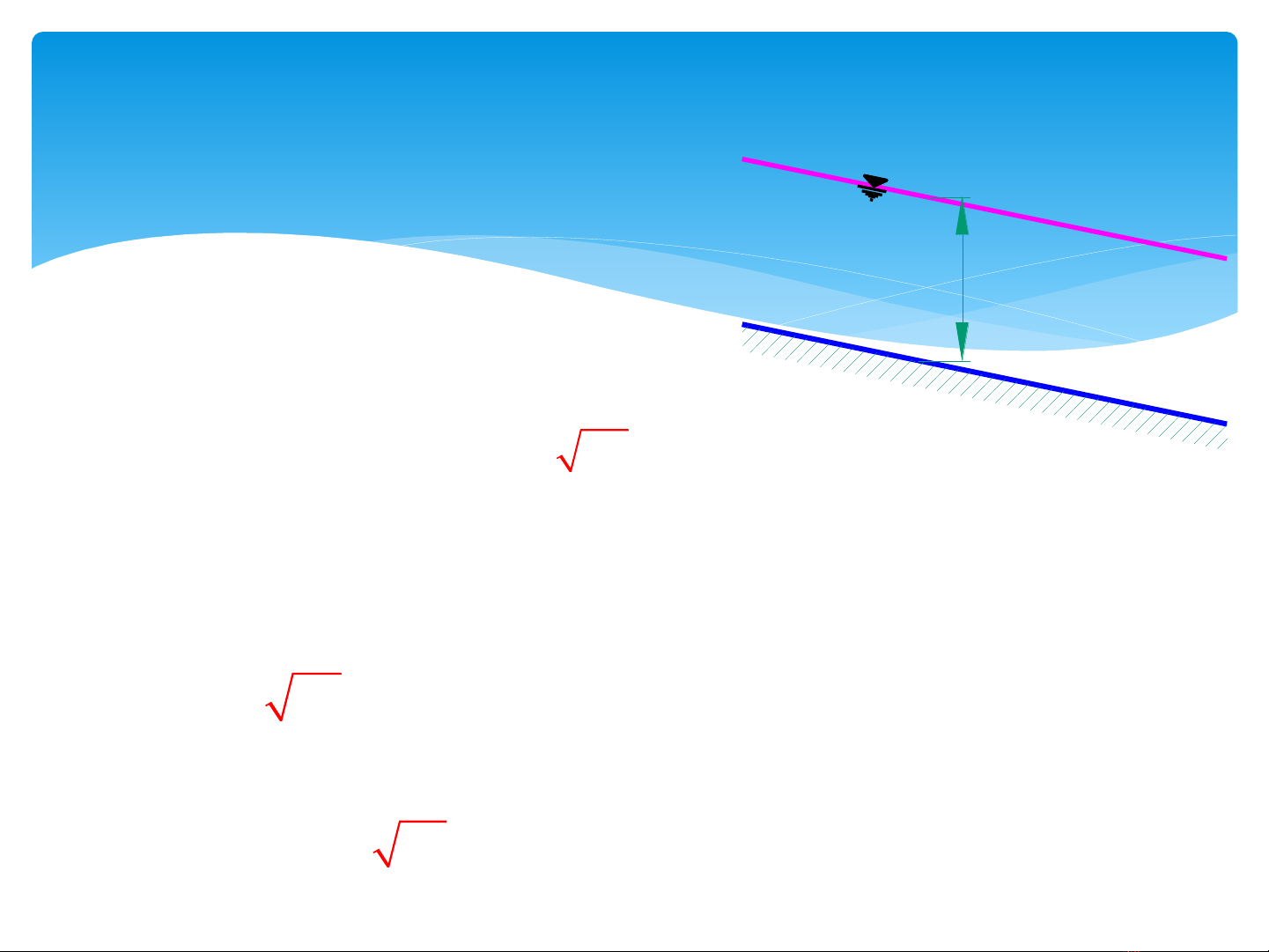
h0
J
i


























